素养模块检测
一、刷速度
1.某游戏项目中,挑战者小明需要利用绳子荡过水坑,如图所示.两次游戏中小明分别抓住绳子的 $ A $ 点和 $ B $ 点,并随绳子做圆周运动.两次抓住绳瞬间速度方向均水平,且大小相等.视小明为质点,比较他抓住 $ A $ 点和抓住 $ B $ 点,抓住 $ A $ 点( )
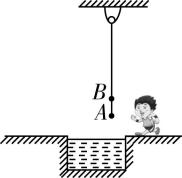
A.对绳子的拉力较大
B.角速度较大
C.向心加速度较小
D.最终能荡到更大的高度
答案:C
解析:小明从最低点以大小相等的速度 $ v $ 做圆周运动,由牛顿第二定律可知 $ T=mg+m\dfrac{{v}^{2}}{l} $ ,抓住 $ A $ 点时的半径 $ l $ 较大,则 $ T $ 较小,由牛顿第三定律可知,抓住 $ A $ 点时对绳子的拉力较小,故 $ \mathrm{A} $ 错误;角速度为 $ \omega =\dfrac{v}{l} $ ,因抓 $ A $ 点时半径 $ l $ 较大,则角速度较小,故 $ \mathrm{B} $ 错误;向心加速度为 $ {a}_{\mathrm{n}}=\dfrac{{v}^{2}}{l} $ ,因抓 $ A $ 点时半径 $ l $ 较大,则向心加速度较小,故 $ \mathrm{C} $ 正确;设荡起的最大高度为 $ ℎ $ ,由动能定理可知 $ -mgℎ=0-\dfrac{1}{2}m{v}^{2} $ ,可得 $ ℎ=\dfrac{{v}^{2}}{2g} $ ,则无论抓住 $ A $ 点还是 $ B $ 点,最终能荡起的最大高度相同,故 $ \mathrm{D} $ 错误.
2.直角侧移门结构可简化成图甲(俯视).玻璃门的两端滑轮 $ A $ 、 $ B $ 通过一根可自由转动的轻杆连接,滑轮可沿直角导轨自由滑动(滑轮视为质点).玻璃门的宽度为 $ L=1\mathrm{m} $ .关门时,拉住把手使滑轮 $ A $ 从初始位置由静止开始做加速度为 $ 1\mathrm{m}/{\mathrm{s}}^{2} $ 的匀加速运动,当滑轮 $ A $ 到达图乙位置时,滑轮 $ B $ 的速度大小为( )
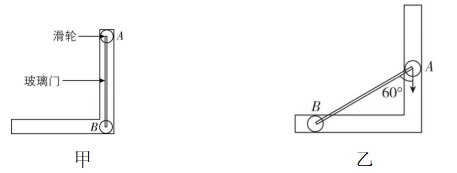
A. $ \dfrac{\sqrt{3}}{3}\mathrm{m}/\mathrm{s} $
B. $ \dfrac{\sqrt{3}}{2}\mathrm{m}/\mathrm{s} $
C. $ 1\mathrm{m}/\mathrm{s} $
D. $ \sqrt{3}\mathrm{m}/\mathrm{s} $
答案:A
解析:拉住把手使滑轮 $ A $ 从初始位置由静止开始做加速度为 $ 1\mathrm{m}/{\mathrm{s}}^{2} $ 的匀加速运动,当滑轮 $ A $ 到达题图乙位置时,对滑轮 $ A $ ,由运动学公式有 $ 2a(L-L \cos {60}^{\circ })={v}_{A}^{2} $ ,解得此时滑轮 $ A $ 的速度大小为 $ {v}_{A}=1\mathrm{m}/\mathrm{s} $ ,滑轮 $ A $ 与滑轮 $ B $ 沿玻璃门方向的分速度大小相等,有 $ {v}_{A} \cos {60}^{\circ }={v}_{B} \cos {30}^{\circ } $ ,解得滑轮 $ B $ 的速度大小为 $ {v}_{B}=\dfrac{\sqrt{3}}{3}\mathrm{m}/\mathrm{s} $ ,故选 $ \mathrm{A} $ .
3.国家航天局发布了我国首次火星探测任务天问一号探测器着陆过程两器分离和着陆后祝融号拍摄的影像.接下来祝融号和轨道相互锁定,在转运机构的作用下,一起被转移到火星表面,假设祝融号和轨道总质量为 $ M $ ,当它们从静止开始,以恒定的加速度竖直下降,下落高度为 $ ℎ $ 时速度为 $ v $ ,若火星表面的重力加速度为 $ g $ ,对于这个过程,下列说法正确的是( )
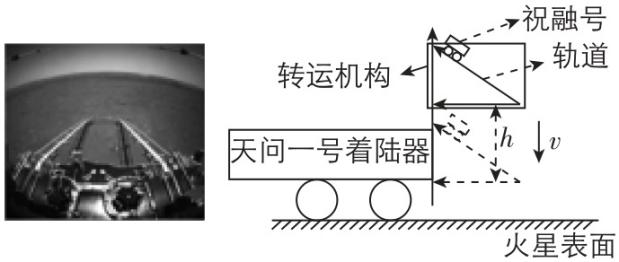
A.重力做功为 $ Mgℎ $ ,重力势能增加了 $ Mgℎ $
B.机械能减少了 $ Mgℎ-\dfrac{1}{2}M{v}^{2} $
C.转运机构做功为 $ Mgℎ+\dfrac{1}{2}M{v}^{2} $
D.合外力做功为 $ \dfrac{1}{2}M{v}^{2}-Mgℎ $
答案:B
解析:祝融号和轨道下落高度为 $ ℎ $ 时,重力做功为 $ Mgℎ $ ,重力势能减少了 $ Mgℎ $ ,故 $ \mathrm{A} $ 错误;重力势能减少了 $ Mgℎ $ ,动能增加了 $ \dfrac{1}{2}M{v}^{2} $ ,则机械能减少了 $ Mgℎ-\dfrac{1}{2}M{v}^{2} $ ,故 $ \mathrm{B} $ 正确;根据功能关系可知,转运机构做功等于机械能减少量,为 $ Mgℎ-\dfrac{1}{2}M{v}^{2} $ ,故 $ \mathrm{C} $ 错误;根据动能定理知,合外力做功等于动能的变化量,为 $ \dfrac{1}{2}M{v}^{2} $ ,故 $ \mathrm{D} $ 错误.
4.如图所示,地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动.地球和太阳的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角).当行星处于最大视角处时,是地球上天文爱好者观察该行星的最佳时期.已知地球公转的轨道半径为 $ R $ ,周期为 $ T $ ,行星的公转轨道半径为 $ r $ ,下列说法正确的是( )
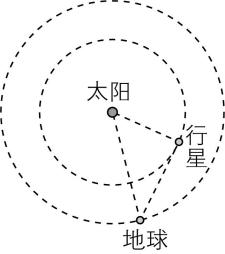
A.该行星的最大视角的余弦值为 $ \dfrac{r}{R} $
B.该行星围绕太阳公转的周期 $ T^\prime =T\sqrt{\dfrac{{r}^{3}}{{R}^{3}}} $
C.该行星与地球绕太阳公转的向心加速度之比 $ \dfrac{{a}_{行}}{{a}_{地}}=\dfrac{{r}^{2}}{{R}^{2}} $
D.若该行星和地球绕太阳逆时针运动,从图示位置开始再经 $ t=T\dfrac{\sqrt{{r}^{3}}}{\sqrt{{R}^{3}-\sqrt{{r}^{3}}}} $ 出现下一次最佳观察时期
答案:B
解析:根据几何关系可知,该行星的最大视角的余弦值为 $ \cos \theta =\dfrac{\sqrt{{R}^{2}-{r}^{2}}}{R} $ ,故 $ \mathrm{A} $ 错误;由开普勒第三定律可得 $ \dfrac{{R}^{3}}{{T}^{2}}=\dfrac{{r}^{3}}{T{\prime }^{2}} $ ,解得 $ T^\prime =T\sqrt{\dfrac{{r}^{3}}{{R}^{3}}} $ ,故 $ \mathrm{B} $ 正确;根据万有引力提供向心力有 $ \dfrac{GMm}{r{\prime }^{2}}=ma $ ,可知该行星与地球绕太阳公转的向心加速度之比 $ \dfrac{{a}_{行}}{{a}_{地}}=\dfrac{{R}^{2}}{{r}^{2}} $ ,故 $ \mathrm{C} $ 错误;当该行星处于紧接着的下一次最佳观察期时,地球在该行星之前,设地球的角速度为 $ {\omega }_{1} $ ,行星的角速度为 $ {\omega }_{2} $ ,经历时间为 $ t $ ,有 $ {\omega }_{2}t-{\omega }_{1}t=2\mathrm{\pi }-2(\dfrac{\mathrm{\pi }}{2}-\theta )=\mathrm{\pi }+2\theta $ ,解得 $ t=T\dfrac{(\mathrm{\pi }+2\theta )\sqrt{{r}^{3}}}{2\mathrm{\pi }(\sqrt{{R}^{3}}-\sqrt{{r}^{3}})} $ ,故 $ \mathrm{D} $ 错误.
5.如图所示,楔形木块 $ abc $ 固定在水平面上,粗糙斜面 $ ab $ 和 $ bc $ 与水平面的夹角相同,顶角 $ b $ 处安装一个定滑轮.质量分别为 $ M $ 、 $ m(M > m) $ 的滑块1、2通过不可伸长的轻绳跨过定滑轮连接,轻绳与斜面平行.两滑块由静止释放后,沿斜面做匀加速运动.若不计滑轮的质量和摩擦,在两滑块沿斜面运动的过程中( )
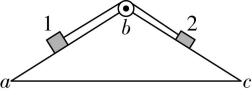
A.轻绳对滑块2做的功等于滑块2增加的机械能
B.重力对滑块1做的功小于滑块1减少的重力势能
C.轻绳对滑块2做的功等于滑块2增加的动能与滑块2克服摩擦力所做的功之和
D.两滑块与轻绳组成的系统损失的机械能等于滑块1、2克服摩擦力所做的功之和
答案:D
解析:根据能量守恒定律可知,轻绳对滑块2做的功等于滑块2增加的机械能与滑块2克服摩擦力所做的功之和,即轻绳对滑块2做的功大于滑块2增加的机械能,故 $ \mathrm{A} $ 、 $ \mathrm{C} $ 错误;根据重力做功与重力势能变化量的关系可知,重力对滑块1做的功等于滑块1减少的重力势能,故 $ \mathrm{B} $ 错误;根据功能关系可知,两滑块与轻绳组成的系统损失的机械能等于滑块1、2克服摩擦力所做的功之和,故 $ \mathrm{D} $ 正确.
6.一种升降电梯的原理图如图甲, $ A $ 为电梯的轿厢, $ B $ 为平衡配重.在某次运行时 $ A $ (含乘客)的质量为 $ {m}_{A}=1000\mathrm{k}\mathrm{g} $ 、 $ B $ 的质量为 $ {m}_{B}=600\mathrm{k}\mathrm{g} $ . $ A $ 、 $ B $ 由跨过轻质滑轮的足够长轻质缆绳连接.电动机通过牵引绳向下拉配重 $ B $ ,使得电梯的轿厢 $ A $ 由静止开始向上运动(轿厢 $ A $ 、配重 $ B $ 一直未与滑轮相撞).不计空气阻力和摩擦阻力,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .轿厢 $ A $ 向上运动过程中的 $ v-t $ 图像如图乙.下列说法正确的是( )
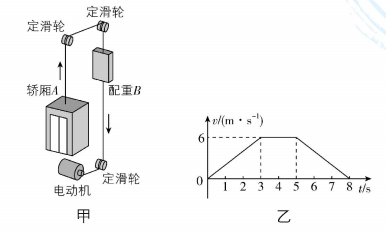
A. $ 0\sim 3\mathrm{s} $ 内配重 $ B $ 处于超重状态
B. $ 3\sim 5\mathrm{s} $ 内电动机所做的功等于 $ 4.8×{10}^{4}\mathrm{J} $
C. $ 5\sim 8\mathrm{s} $ 内轿厢 $ A $ 的加速度大小为 $ 0.75\mathrm{m}/{\mathrm{s}}^{2} $
D. $ 0\sim 8\mathrm{s} $ 内 $ A $ 、 $ B $ 间的缆绳对轿厢 $ A $ 做功的最大功率为 $ 6.0×{10}^{4}\mathrm{W} $
答案:B
解析:由题图乙可知 $ 0\sim 3\mathrm{s} $ 内,轿厢 $ A $ 向上加速运动,加速度向上,配重 $ B $ 向下加速运动,加速度向下,则配重 $ B $ 处于失重状态,故 $ \mathrm{A} $ 错误; $ v-t $ 图像中图线与 $ t $ 轴围成的图形面积表示位移, $ 3\sim 5\mathrm{s} $ 内,轿厢的位移大小为 $ x=6×2\mathrm{m}=12\mathrm{m} $ , $ 3\sim 5\mathrm{s} $ 内,根据动能定理有 $ W+{m}_{B}gx-{m}_{A}gx=0 $ ,解得 $ 3\sim 5\mathrm{s} $ 内电动机所做的功为 $ W=4.8×{10}^{4}\mathrm{J} $ ,故 $ \mathrm{B} $ 正确; $ 5\sim 8\mathrm{s} $ 内,轿厢 $ A $ 的加速度大小为 $ a=\dfrac{\mathrm{\Delta }v}{\mathrm{\Delta }t}=\dfrac{6}{3}\mathrm{m}/{\mathrm{s}}^{2}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{C} $ 错误; $ 0\sim 3\mathrm{s} $ 内,轿厢 $ A $ 的加速度大小为 $ {a}_{1}=\dfrac{\mathrm{\Delta }{v}_{1}}{\mathrm{\Delta }{t}_{1}}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,设 $ A $ 、 $ B $ 间的缆绳拉力大小为 $ F $ ,对轿厢 $ A $ ,根据牛顿第二定律有 $ F-{m}_{A}g={m}_{A}{a}_{1} $ ,解得 $ F=1.2×{10}^{4}\mathrm{N} $ , $ 3\mathrm{s} $ 时,轿厢 $ A $ 的速度最大, $ A $ 、 $ B $ 间的缆绳拉力最大,则 $ 0\sim 8\mathrm{s} $ 内, $ 3\mathrm{s} $ 时缆绳对轿厢 $ A $ 做功的功率最大,为 $ P=Fv=7.2×{10}^{4}\mathrm{W} $ ,故 $ \mathrm{D} $ 错误.
7.如图所示为速冻食品加工厂生产和包装饺子的一道工序.将饺子轻放在以速度 $ {v}_{0} $ 匀速运动的足够长的水平传送带上,饺子与传送带间的动摩擦因数为 $ \mu $ ,重力加速度为 $ g $ .不考虑饺子之间的相互作用和空气阻力.关于饺子在传送带上的运动,下列说法正确的是( )

A.饺子在传送带上始终受重力、弹力和摩擦力的作用
B.传送带的速度越大,饺子的加速度越大
C.饺子在传送带上留下的痕迹长度为 $ \dfrac{{v}_{0}^{2}}{\mu g} $
D.饺子在运动过程中,增加的动能与因摩擦产生的热量相等
答案:D
解析:饺子刚放到传送带上时在传送带上受重力、弹力和摩擦力的作用,与传送带共速后受重力和弹力作用,故 $ \mathrm{A} $ 错误;由牛顿第二定律得饺子加速运动时的加速度 $ a=\dfrac{\mu mg}{m}=\mu g $ ,与传送带的速度无关,故 $ \mathrm{B} $ 错误;饺子从放上传送带到与传送带共速所用时间 $ t=\dfrac{{v}_{0}}{\mu g} $ ,饺子在传送带上留下的痕迹长度为 $ \mathrm{\Delta }s={v}_{0}t-\dfrac{{v}_{0}}{2}t=\dfrac{{v}_{0}^{2}}{2\mu g} $ ,故 $ \mathrm{C} $ 错误;饺子在运动过程中,增加的动能 $ \mathrm{\Delta }{E}_{\mathrm{k}}=\dfrac{1}{2}m{v}_{0}^{2} $ ,因摩擦产生的热量 $ Q=\mu mg\mathrm{\Delta }s=\dfrac{1}{2}m{v}_{0}^{2} $ ,可知 $ \mathrm{\Delta }{E}_{\mathrm{k}}=Q $ ,故 $ \mathrm{D} $ 正确.
8.如图所示,置于竖直平面内呈抛物线形状的 $ AB $ 光滑细杆,它是按照初速度为 $ {v}_{0} $ ,水平射程为 $ s $ 的平抛运动轨迹的形状制成的,其中 $ A $ 端对应抛出点,离地面的高度为 $ s $ , $ B $ 端为着地点.现将一质量为 $ m $ 可视为质点的小球套于光滑细杆上,由静止开始从 $ A $ 端滑下,不计空气阻力,重力加速度为 $ g $ .则当小球到达细杆的 $ B $ 端时(未触地)( )
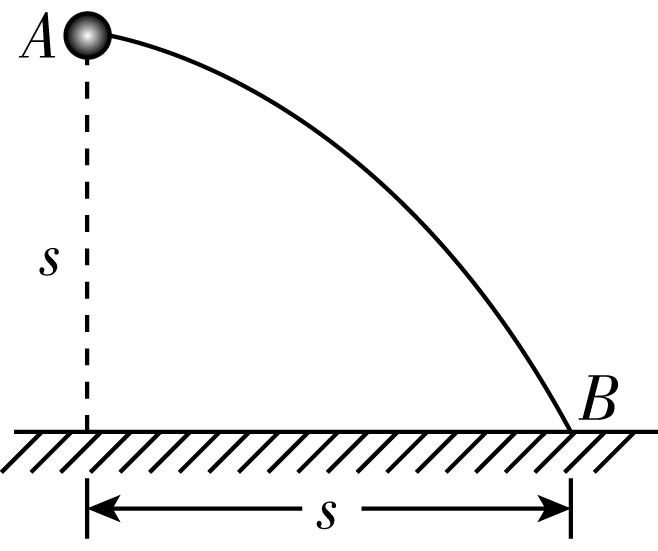 (多选)
(多选)
A. 小球在水平方向的速度大小为 $ {v}_{0} $
B. 小球的瞬时速率为 $ 2{v}_{0} $
C. 小球的速度方向与水平方向的夹角为 $ {45}^{\circ } $
D. 小球重力的瞬时功率为 $ \dfrac{4}{5}\mathrm{ }\sqrt{5}mg{v}_{0} $
答案:BD
解析:若小球以初速度 $ {v}_{0} $ 做平抛运动,则 $ s=\dfrac{1}{2}g{t}^{2} $ , $ s={v}_{0}t $ ,可得 $ s=\dfrac{2{v}_{0}^{2}}{g} $ ,细杆B端的切线与水平方向的夹角满足 $ \tan \mathrm{ }\theta =\dfrac{{v}_{y}}{{v}_{0}}=\dfrac{gt}{{v}_{0}}=2 $ ,设小球沿细杆运动到B端时的速率为 $ {v}_{B} $ ,根据动能定理得 $ mgs=\dfrac{1}{2}m{v}_{B}^{2} $ ,解得到达B端时(未触地)小球的瞬时速率为 $ {v}_{B}=\sqrt{2gs}=2{v}_{0} $ ,小球运动到B端时,在水平方向的速度大小 $ {v}_{1}={v}_{B} \cos \mathrm{ }\theta =\dfrac{2\sqrt{5}}{5}{v}_{0} $ ,故A错误,B正确;到达B端时(未触地)小球的速度方向与水平方向夹角和在细杆B端的切线与水平方向的夹角相同,则 $ \tan \mathrm{ }\theta =2 $ , $ \theta $ 不等于 $ {45}^{\circ } $ ,故C错误;到达B端(未触地)瞬间小球重力的功率为 $ {P}_{G}=mg{v}_{B} \sin \mathrm{ }\theta =\dfrac{4}{5}\mathrm{ }\mathrm{ }\sqrt{5}mg{v}_{0} $ ,故D正确.
9.如图,在万有引力作用下, $ a $ 、 $ b $ 两卫星在同一平面内绕某一行星 $ c $ 沿逆时针方向做匀速圆周运动,轨道半径之比为 $ {r}_{a}:{r}_{b}=1:2 $ ,已知 $ \mathrm{\angle }acb={90}^{\circ } $ , $ \sqrt{2}\approx 1.414 $ .则下列说法正确的是( )
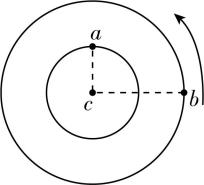 (多选)
(多选)
A. $ a $ 、 $ b $ 运动的向心加速度之比为 $ {a}_{a}:{a}_{b}=4:1 $
B. $ a $ 、 $ b $ 运动的向心加速度之比为 $ {a}_{a}:{a}_{b}=8:1 $
C.从图示位置开始,在 $ b $ 转动一周的过程中, $ a $ 、 $ b $ 、 $ c $ 共线3次
D.从图示位置开始,在 $ b $ 转动一周的过程中, $ a $ 、 $ b $ 、 $ c $ 共线4次
答案:AD
解析:根据 $ G\dfrac{Mm}{{r}^{2}}=ma $ ,可知 $ a=\dfrac{GM}{{r}^{2}} $ , $ a $ 、 $ b $ 运动的向心加速度之比为 $ {a}_{a}:{a}_{b}=4:1 $ , $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;根据开普勒第三定律, $ a $ 、 $ b $ 的周期之比 $ \dfrac{{T}_{a}}{{T}_{b}}=\sqrt{{\left(\dfrac{{r}_{a}}{{r}_{b}}\right) ^ {3}}}=\dfrac{\sqrt{2}}{4} $ ,设经时间 $ t $ 时三者共线,则 $ \dfrac{2\mathrm{\pi }t}{{T}_{a}}-\dfrac{2\mathrm{\pi }t}{{T}_{b}}=\dfrac{\mathrm{\pi }}{2}(2n+1)(n=0,1,2,3,\cdots ) $ ,当 $ t={T}_{b} $ 时可得 $ n=3.16 $ ,可知从题图所示位置开始,在 $ b $ 转动一周的过程中, $ a $ 、 $ b $ 、 $ c $ 共线4次,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
10.如图所示,一根轻质弹簧与质量为 $ m $ 的滑块 $ P $ 连接后,穿在一根光滑竖直杆上,弹簧下端与竖直杆的下端连接,一根轻绳跨过定滑轮将滑块 $ P $ 和重物 $ Q $ 连接起来.图中 $ O $ 、 $ B $ 两点等高,线段 $ OA $ 长为 $ L $ ,与水平方向的夹角 $ \theta ={37}^{\circ } $ ,重物 $ Q $ 的质量 $ M=5m $ ,把滑块从图中 $ A $ 点由静止释放后沿竖直杆上下运动,当它经过 $ A $ 、 $ B $ 两点时,弹簧对滑块的弹力大小相等,不计滑轮的摩擦,重力加速度为 $ g $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ .在滑块从 $ A $ 到 $ B $ 的运动过程中,下列说法正确的是( )
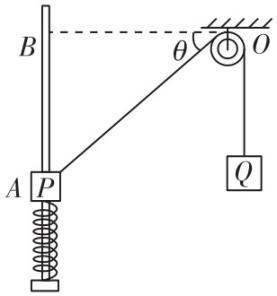 (多选)
(多选)
A.滑块的速度一直增大
B.轻绳对滑块做功为 $ 0.5mgL $
C.滑块在位置 $ B $ 的速度大小 $ {v}_{B}=\sqrt{\dfrac{4}{5}gL} $
D. $ P $ 与 $ Q $ 的机械能之和先增大后减小
答案:CD
解析:由经过 $ A $ 、 $ B $ 两点时弹簧对滑块的弹力大小相等可知,滑块在 $ A $ 点弹簧处于压缩状态,滑块在 $ B $ 点弹簧处于伸长状态,滑块在 $ B $ 点所受合力竖直向下,则滑块在靠近 $ B $ 点过程中必有所受合力方向竖直向下的阶段,该阶段滑块的速度减小,故 $ \mathrm{A} $ 错误;滑块在 $ A $ 、 $ B $ 两点时,弹簧对滑块的弹力大小相等,即弹簧的形变量相等,弹簧的弹性势能相等,滑块运动到 $ B $ 点时,重物的速度为零,对系统,由机械能守恒定律可得 $ 5mg(L-L \cos {37}^{\circ })=mgL \sin {37}^{\circ }+\dfrac{1}{2}m{v}_{B}^{2} $ ,解得 $ {v}_{B}=\sqrt{\dfrac{4}{5}gL} $ ,因为滑块在 $ A $ 、 $ B $ 两点弹簧弹性势能相等,即弹簧对滑块做功为零,所以轻绳对滑块做的功等于滑块增加的机械能,则 $ W=mgL \sin {37}^{\circ }+\dfrac{1}{2}m{v}_{B}^{2}=mgL $ ,故 $ \mathrm{B} $ 错误, $ \mathrm{C} $ 正确;由 $ \mathrm{A} $ 选项分析可知,滑块从 $ A $ 点到 $ B $ 点过程中弹簧对 $ P $ 、 $ Q $ 整体先做正功,后做负功,所以 $ P $ 与 $ Q $ 的机械能之和先增大后减小,故 $ \mathrm{D} $ 正确.
11.(10分)如图甲所示,科学家设想通过环形空间站绕中心旋转模拟地球表面重力场的环境.某物理小组设计了如图乙所示的实验装置验证空间站人造重力场下的“机械能守恒定律”.
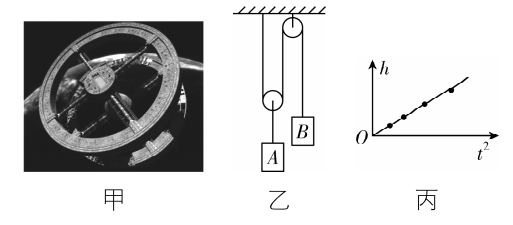
(1) 设环形空间站的旋转半径为 $ r $ ,角速度为 $ \omega $ ,则等效重力加速度 $ g= $ ;
(2) 按图乙组装好器材后,将 $ A $ 由静止释放.测出 $ B $ 上升的高度 $ h $ 及所用的时间 $ t $ ,为使 $ B $ 上升, $ A $ 的质量 $ {m}_{A} $ 与 $ B $ 的质量 $ {m}_{B} $ 之间的关系应满足 ;
(3) 若在误差允许范围内,关系式 $ {m}_{A}g\cdot \dfrac{h}{2}-{m}_{B}gh= $ (用 $ {m}_{A} $ 、 $ {m}_{B} $ 、 $ h $ 、 $ t $ 表示)成立,则成功验证了“机械能守恒定律”;
(4) 为使实验更精确,实验中多次测量得到 $ h $ 与 $ {t}^{2} $ 数据,绘制 $ h-{t}^{2} $ 图像,如图丙所示,图像斜率 $ k= $ (用 $ {m}_{A} $ 、 $ {m}_{B} $ 、 $ g $ 表示).
答案:(1) $ {\omega }^{2}r $
(2) $ {m}_{A} > 2{m}_{B} $
(3) $ \dfrac{{m}_{A}{h}^{2}}{2{t}^{2}}+\dfrac{2{m}_{B}{h}^{2}}{{t}^{2}} $
(4) $ \dfrac{({m}_{A}-2{m}_{B})g}{{m}_{A}+4{m}_{B}} $
解析:(1) 环形空间站处于完全失重状态,若环形空间站的旋转半径为 $ r $ ,角速度为 $ \omega $ ,则等效重力加速度 $ g={\omega }^{2}r $ .
(2) 使 $ B $ 上升,即使 $ A $ 下降,根据滑轮的特征可知, $ A $ 的质量 $ {m}_{A} $ 与 $ B $ 的质量 $ {m}_{B} $ 之间的关系应满足 $ {m}_{A} > 2{m}_{B} $ .
(3) 对 $ A $ 、 $ B $ 组成的系统, $ B $ 上升 $ h $ 过程,根据系统机械能守恒有 $ {m}_{A}g\cdot \dfrac{h}{2}-{m}_{B}gh=\dfrac{1}{2}{m}_{A}{v}_{A}^{2}+\dfrac{1}{2}{m}_{B}{v}_{B}^{2} $ ,其中 $ {v}_{B}=2{v}_{A} $ , $ h=\dfrac{{v}_{B}}{2}t $ ,解得 $ {m}_{A}g\cdot \dfrac{h}{2}-{m}_{B}gh=\dfrac{{m}_{A}{h}^{2}}{2{t}^{2}}+\dfrac{2{m}_{B}{h}^{2}}{{t}^{2}} $ .
(4) 结合上述可以解得 $ h=\dfrac{({m}_{A}-2{m}_{B})g}{{m}_{A}+4{m}_{B}}{t}^{2} $ ,可知 $ h-{t}^{2} $ 图像的斜率 $ k=\dfrac{({m}_{A}-2{m}_{B})g}{{m}_{A}+4{m}_{B}} $ .
12.(12分)如图所示,质量均为 $ m $ 的套筒 $ A $ 和小球 $ B $ 通过长度为 $ L $ 的轻杆及铰链连接,套筒 $ A $ 套在竖直立杆 $ OP $ 上与原长为 $ L $ 的轻质弹簧连接,小球 $ B $ 可以沿水平槽滑动,系统静止时轻杆与竖直方向夹角 $ \theta ={37}^{\circ } $ .现让系统从静止绕 $ OP $ 缓慢加速转动,某时刻 $ B $ 球对槽恰好无压力.已知重力加速度为 $ g $ ,弹簧始终在弹性限度内,不计一切摩擦, $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ .求:
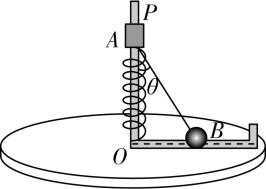
(1) 弹簧的劲度系数 $ k $ ;
(2) $ B $ 球对槽恰好无压力时系统转动的角速度 $ \omega $ ;
(3) 从静止开始至 $ B $ 球对槽无压力过程中槽对 $ B $ 球做的功.
答案:(1) $ \dfrac{5mg}{L} $
(2) $ \sqrt{\dfrac{5g}{3L}} $
(3) $ \dfrac{19}{30}mgL $
解析:(1) 系统静止时,根据平衡条件有 $ k(L-L \cos {37}^{\circ })=mg $ ,解得 $ k=\dfrac{5mg}{L} $ .
(2) $ B $ 球对槽恰好无压力时,设此时弹簧的压缩量为 $ \mathrm{\Delta }x $ ,对整体分析有 $ k\mathrm{\Delta }x=2mg $ ,解得 $ \mathrm{\Delta }x=\dfrac{2}{5}L $ ,
根据几何关系有 $ \cos \theta \prime =\dfrac{L-\mathrm{\Delta }x}{L}=\dfrac{3}{5} $ ,解得 $ \theta \prime ={53}^{\circ } $ ,
对 $ B $ 球,根据牛顿第二定律可得 $ mg \tan \theta \prime ={\rm mL} \sin \theta \prime \cdot {\omega }^{2} $ ,解得 $ \omega =\sqrt{\dfrac{5g}{3L}} $ .
(3) 对 $ A $ ,由动能定理可得 $ {W}_{杆}+{W}_{G}+{W}_{弹}=0 $ ,即 $ {W}_{杆}+mg\cdot \dfrac{1}{5}L-\dfrac{mg+2mg}{2}\cdot \dfrac{1}{5}L=0 $ ,解得 $ {W}_{杆}=0.1mgL $ ,
对 $ B $ 球,由动能定理可得 $ {W}_{外}+W{\prime }_{杆}=\dfrac{1}{2}m{v}^{2} $ ,其中 $ W{\prime }_{杆}=-{W}_{杆} $ , $ v=\omega L \sin {53}^{\circ } $ ,联立解得 $ {W}_{外}=\dfrac{19}{30}mgL $ .
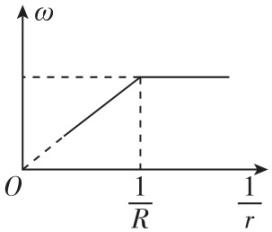
13.(14分)螺旋星系中有大量的恒星和星际物质,主要分布在半径为 $ R $ 的球体内,球体外仅有极少的恒星.球体内物质总质量为 $ M $ ,可认为均匀分布,球体内外的所有恒星都绕星系中心做匀速圆周运动,恒星到星系中心的距离为 $ r $ ,引力常量为 $ G $ .
(1) 求 $ r > R $ 区域的恒星做匀速圆周运动的角速度大小 $ \omega $ 与 $ r $ 的关系;
(2) 已知质量分布均匀的球壳对壳内物体的万有引力为零.求 $ r⩽ R $ 区域的恒星做匀速圆周运动的角速度大小 $ {\omega }_{0} $ ;
(3) 科学家根据实测数据,得到此螺旋星系中不同位置的恒星做匀速圆周运动的角速度大小 $ \omega $ 随 $ \dfrac{1}{r} $ 的变化关系图像,如图所示.根据在 $ r > R $ 范围内的恒星角速度大小与距离 $ r $ 的倒数成正比,科学家预言螺旋星系周围 $ (r > R) $ 存在一种特殊物质,称为暗物质.暗物质与通常的物质有引力相互作用,并遵循万有引力定律,求 $ r=nR $ 内暗物质的质量 $ M^\prime $ .
答案:(1) $ \omega =\sqrt{\dfrac{GM}{{r}^{3}}} $
(2) $ \sqrt{\dfrac{GM}{{R}^{3}}} $
(3) $ (n-1)M $
解析:(1) 恒星绕星系中心做匀速圆周运动,对恒星有
$ G\dfrac{Mm}{{r}^{2}}=mr{\omega }^{2} $ ,解得 $ \omega =\sqrt{\dfrac{GM}{{r}^{3}}} $ .
(2) 设星系密度为 $ \rho $ ,在 $ r⩽ R $ 区域,对恒星,万有引力提供向心力,有 $ G\dfrac{{M}_{0}m}{{r}^{2}}=mr{\omega }_{0}^{2} $ ,其中 $ {M}_{0}=\rho \cdot \dfrac{4}{3}\mathrm{\pi }{r}^{3} $ ,
又因为整个球体的质量为 $ M=\rho \cdot \dfrac{4}{3}\mathrm{\pi }{R}^{3} $ ,
联立解得 $ {\omega }_{0}=\sqrt{\dfrac{GM}{{R}^{3}}} $ .
(3) 在 $ r > R $ 区域,万有引力提供向心力,有 $ G\dfrac{(M+M^\prime )m}{{r}^{2}}=m{\omega }^{2}r $ ,又 $ G\dfrac{Mm}{{R}^{2}}=mR{\omega }_{0}^{2} $ ,
根据题意有 $ \omega =k\dfrac{1}{r} $ , $ {\omega }_{0}=k\dfrac{1}{R} $ , $ r=nR $ ,解得 $ M^\prime =(n-1)M $ .
14.(18分)如图所示,半径 $ R=1\mathrm{m} $ 的光滑圆弧轨道 $ BCD $ 固定在竖直平面内,轨道的上端点 $ B $ 和圆心 $ O $ 的连线与水平方向的夹角 $ \theta ={30}^{\circ } $ , $ OC $ 与 $ OB $ 关于水平方向对称, $ D $ 点为圆弧轨道的最低点,与粗糙水平面相切(平滑连接),一轻质弹簧的右端固定在竖直挡板上.质量 $ m=1\mathrm{k}\mathrm{g} $ 、可视为质点的小物块从空中 $ A $ 点以 $ {v}_{0}=2\mathrm{m}/\mathrm{s} $ 的速度水平抛出,恰好从 $ B $ 点沿轨道切线方向进入轨道,经过圆弧轨道上 $ D $ 点后沿水平面向右运动至 $ E $ 点时,弹簧被压缩至最短,小物块第二次到达 $ D $ 点时刚好停止运动,不计空气阻力,弹簧始终在弹性限度内,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ .求:
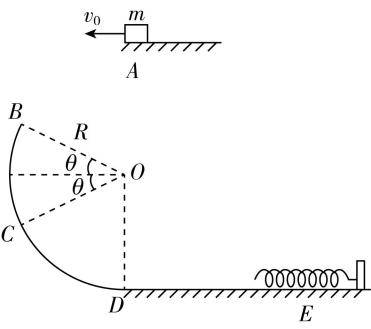
(1) 小物块运动到 $ B $ 点时的速度大小;
(2) 小物块经过 $ C $ 点时对轨道的压力大小;
(3) 整个过程中弹簧弹性势能的最大值 $ {E}_{\mathrm{p}\mathrm{m}} $ .
答案:(1) $ 4\mathrm{m}/\mathrm{s} $
(2) $ 41\mathrm{N} $
(3) $ 11.5\mathrm{J} $
解析:(1) 小物块恰好从 $ B $ 点沿切线方向进入轨道,由几何关系有 $ {v}_{B}=\dfrac{{v}_{0}}{ \sin \theta } $ ,
解得 $ {v}_{B}=4\mathrm{m}/\mathrm{s} $ .
(2) 小物块由 $ B $ 点运动到 $ C $ 点,由动能定理得
$ 2mgR \sin \theta =\dfrac{1}{2}m{v}_{C}^{2}-\dfrac{1}{2}m{v}_{B}^{2} $ ,
在 $ C $ 点,由牛顿第二定律有 $ {F}_{\mathrm{N}}-mg \sin \theta =m\dfrac{{v}_{C}^{2}}{R} $ ,
解得 $ {F}_{\mathrm{N}}=41\mathrm{N} $ ,
根据牛顿第三定律,小物块经过圆弧轨道上 $ C $ 点时对轨道的压力大小 $ F{\prime }_{\mathrm{N}}={F}_{\mathrm{N}}=41\mathrm{N} $ .
(3) 小物块由 $ B $ 点运动到 $ D $ 点,由机械能守恒定律有
$ \dfrac{1}{2}m{v}_{B}^{2}+mgR(1+ \sin \theta )=\dfrac{1}{2}m{v}_{D}^{2} $ ,
小物块从 $ D $ 点运动到 $ E $ 点,由能量守恒定律有
$ \dfrac{1}{2}m{v}_{D}^{2}={W}_{f}+{E}_{\mathrm{p}\mathrm{m}} $ ,
小物块从 $ E $ 点运动到 $ D $ 点,由能量守恒定律有 $ {E}_{\mathrm{p}\mathrm{m}}={W}_{f} $ ,
解得 $ {E}_{\mathrm{p}\mathrm{m}}=11.5\mathrm{J} $ .







 (多选)
(多选) (多选)
(多选) (多选)
(多选)


