第2节 重力势能
一、刷基础
1.如图所示,三个斜面的高度相同,倾角 $ {\theta }_{1} < {\theta }_{2} < {\theta }_{3} $ ,质量相同的小物块 $ A $ 、 $ B $ 、 $ C $ 分别沿三个斜面从顶端由静止下滑到底端,已知小物块与斜面间的动摩擦因数均相同.则( )
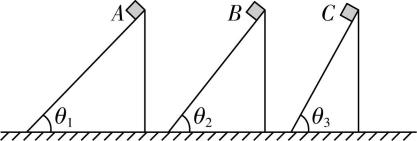
A.重力对 $ A $ 物块做的功最多
B.摩擦力对 $ C $ 物块做的功最多
C.重力对 $ B $ 物块做功的平均功率最大
D.到达斜面底端时 $ C $ 物块重力的功率最大
答案:D
解析:物块下滑的高度相同,根据 $ {W}_{G}=mgh $ ,可知三物块重力做功相同,故 $ \mathrm{A} $ 错误;摩擦力对物块做功为 $ {W}_{f}=-\mu mg \cos \theta \cdot \dfrac{h}{ \sin \theta }=-\dfrac{\mu mgh}{ \tan \theta } $ ,又 $ {\theta }_{1} < {\theta }_{2} < {\theta }_{3} $ ,可知摩擦力对 $ C $ 物块做功最少,故 $ \mathrm{B} $ 错误;根据牛顿第二定律得,物块下滑的加速度大小 $ a=\dfrac{mg \sin \theta -\mu mg \cos \theta }{m}=g \sin \theta -\mu g \cos \theta $ ,可知 $ \theta $ 越大,加速度越大,沿斜面运动的位移 $ x=\dfrac{h}{ \sin \theta } $ 越小,根据 $ x=\dfrac{1}{2}a{t}^{2} $ ,可知运动时间越短,因为 $ {\theta }_{1} < {\theta }_{2} < {\theta }_{3} $ ,则 $ {t}_{1} > {t}_{2} > {t}_{3} $ ,根据 $ \overline{P}=\dfrac{{W}_{G}}{t} $ ,可知 $ {\overline{P}}_{1} < {\overline{P}}_{2} < {\overline{P}}_{3} $ ,故 $ \mathrm{C} $ 错误;由前面分析,根据 $ {v}^{2}=2ax $ 可得 $ v=\sqrt{2gh-\dfrac{2\mu gh}{ \tan \theta }} $ ,可知 $ \theta $ 越大,物块到达斜面底端时速度越大,所以下滑到底端时 $ C $ 物块的速度最大,根据重力的瞬时功率 $ P=mgv \sin \theta $ ,又 $ {\theta }_{1} < {\theta }_{2} < {\theta }_{3} $ ,可知到达斜面底端时 $ C $ 物块重力的功率最大,故 $ \mathrm{D} $ 正确.
2.如图所示,一同学从同一位置将质量相同的飞镖先后以速度 $ {v}_{A} $ 和 $ {v}_{B} $ 水平抛出,分别落在水平地面上的 $ A $ 、 $ B $ 两点,飞镖在空中运动的时间分别为 $ {t}_{A} $ 和 $ {t}_{B} $ ,运动过程中的加速度大小分别为 $ {a}_{A} $ 和 $ {a}_{B} $ ,重力做的功分别为 $ {W}_{A} $ 和 $ {W}_{B} $ ,不计空气阻力,则( )
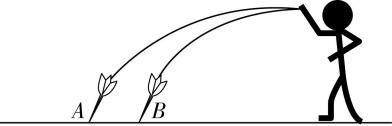
A. $ {v}_{A} > {v}_{B} $
B. $ {W}_{A} > {W}_{B} $
C. $ {t}_{A} > {t}_{B} $
D. $ {a}_{A} > {a}_{B} $
答案:A
解析:两飞镖抛出后均做平抛运动,则加速度均为重力加速度,即 $ {a}_{A}={a}_{B}=g $ , $ \mathrm{D} $ 错误;两飞镖从同一高度飞出,根据 $ t=\sqrt{\dfrac{2h}{g}} $ ,可知 $ {t}_{A}={t}_{B} $ , $ \mathrm{C} $ 错误;根据 $ {v}_{0}=\dfrac{x}{t} $ ,可知 $ {v}_{A} > {v}_{B} $ , $ \mathrm{A} $ 正确;根据 $ W=mgh $ ,可知 $ {W}_{A}={W}_{B} $ , $ \mathrm{B} $ 错误.
3.将横截面积为 $ S $ 的玻璃管弯成如图所示的连通器,放在水平桌面上,左、右管处在竖直状态,先关闭阀门 $ \mathrm{K} $ ,往左、右管中分别注入高度为 $ {h}_{2} $ 和 $ {h}_{1} $ 、密度为 $ \rho $ 的液体,然后打开阀门 $ \mathrm{K} $ ,直到液体静止,重力加速度为 $ g $ ,则重力对液体做的功为( )
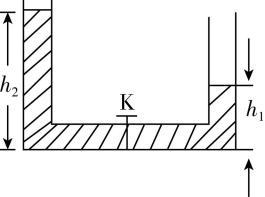
A. $ \rho gS({h}_{2}-{h}_{1}) $
B. $ \dfrac{1}{4}\rho gS({h}_{2}-{h}_{1}) $
C. $ \dfrac{1}{4}\rho gS({h}_{2}-{h}_{1})^{2} $
D. $ \dfrac{1}{2}\rho gS({h}_{2}-{h}_{1})^{2} $
答案:C
解析:当液体重新静止时,此过程可等效为左边高度为 $ \dfrac{1}{2}({h}_{2}-{h}_{1}) $ 的液体由左边最高的位置移到了右边液体的上面,则重心下降的高度为 $ \dfrac{1}{2}({h}_{2}-{h}_{1}) $ ,故重力对液体做的功为 $ {W}_{G}=\rho S\cdot \dfrac{1}{2} ({h}_{2}-{h}_{1} )g\cdot \dfrac{1}{2} ({h}_{2}-{h}_{1} )=\dfrac{1}{4}\rho gS ({h}_{2}-{h}_{1})^{2} $ ,故 $ \mathrm{C} $ 正确.
4.下列关于重力势能的说法中正确的是( )(多选)
A.重力势能 $ {E}_{\mathrm{p}1}=5\mathrm{J} $ , $ {E}_{\mathrm{p}2}=-8\mathrm{J} $ ,则 $ {E}_{\mathrm{p}1} $ 与 $ {E}_{\mathrm{p}2} $ 方向相反
B.同一物体重力势能 $ {E}_{\mathrm{p}1}=5\mathrm{J} $ , $ {E}_{\mathrm{p}2}=-8\mathrm{J} $ ,则 $ {E}_{\mathrm{p}1} > {E}_{\mathrm{p}2} $
C.重力做功和重力势能变化量的关系是 $ {W}_{G}=-\mathrm{\Delta }{E}_{\mathrm{p}} $
D.重力势能的变化量具有相对性
答案:BC
解析:重力势能是标量,没有方向,正值表示物体在零势能参考平面上方,负值表示物体在零势能参考平面下方,同一物体重力势能 $ {E}_{\mathrm{p}1}=5\mathrm{J} $ , $ {E}_{\mathrm{p}2}=-8\mathrm{J} $ ,则有 $ {E}_{\mathrm{p}1} > {E}_{\mathrm{p}2} $ ,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;重力做功和重力势能变化量的关系是 $ {W}_{G}=-\mathrm{\Delta }{E}_{\mathrm{p}} $ ,故 $ \mathrm{C} $ 正确;重力势能具有相对性,但重力势能的变化量没有相对性,故 $ \mathrm{D} $ 错误.
5.一根长为 $ 2\mathrm{m} $ 、重力为 $ 200\mathrm{N} $ 的均匀直木杆放在水平地面上,现将它的一端缓慢地从地面抬高 $ 0.5\mathrm{m} $ ,另一端仍在地面上,则重力势能增加量为( )
A. $ 50\mathrm{J} $
B. $ 100\mathrm{J} $
C. $ 200\mathrm{J} $
D. $ 400\mathrm{J} $
答案:A
解析:在抬高木杆一端的过程中,木杆的重心上升的距离为 $ h=\dfrac{1}{2}×0.5\mathrm{m}=0.25\mathrm{m} $ ,则重力势能增加量为 $ \mathrm{\Delta }{E}_{\mathrm{p}}=Gh=50\mathrm{J} $ , $ \mathrm{A} $ 正确.
6.如图所示,机器狗在泰山进行负重测试,从泰山山脚到目的地用时 $ 2\mathrm{h} $ ,爬升高度为 $ 1200\mathrm{m} $ ,已知机器狗及重物总质量为 $ 100\mathrm{k}\mathrm{g} $ ,重力加速度 $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ ,则机器狗在本次测试中( )

A.位移大小一定为 $ 1200\mathrm{m} $
B.克服重力做功为 $ 1.2×{10}^{6}\mathrm{J} $
C.克服重力做功的平均功率为 $ 6×{10}^{5}\mathrm{W} $
D.重力势能减少了 $ 1.2×{10}^{6}\mathrm{J} $
答案:B
解析:由于山坡是倾斜的,机器狗爬升高度为 $ 1200\mathrm{m} $ ,则位移大小大于 $ 1200\mathrm{m} $ ,故 $ \mathrm{A} $ 错误;机器狗克服重力做功为 $ {W}_{克}=mgh=1.2×{10}^{6}\mathrm{J} $ ,则机器狗和货物的重力势能增加了 $ 1.2×{10}^{6}\mathrm{J} $ ,故 $ \mathrm{B} $ 正确, $ \mathrm{D} $ 错误;机器狗克服重力做功的平均功率为 $ \overline{P}=\dfrac{{W}_{克}}{t}\approx 166.7\mathrm{W} $ ,故 $ \mathrm{C} $ 错误.
7.如图所示,一质量为 $ m $ 的物块(可视为质点)静置在水平地面上,物块上竖直安装一根原长为 $ L $ 、劲度系数为 $ k $ 的轻弹簧,现用手竖直向上缓慢拉弹簧的上端 $ P $ 点,直到物块离开地面一段距离后停止向上运动,测得此时 $ P $ 点到水平地面的距离为 $ H $ ,重力加速度为 $ g $ ,弹簧始终在弹性限度内,待整个装置在空中稳定时,下列说法正确的是( )
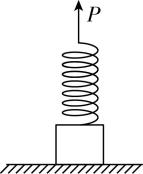 (多选)
(多选)
A.以地面为零势能面,则物块在空中的重力势能为 $ mgH $
B.以此时 $ P $ 点所在平面为零势能面,则物块在空中的重力势能为 $ -mg(L+\dfrac{mg}{k}) $
C.此过程物块重力势能增加了 $ mg(H-L)-\dfrac{{m}^{2}{g}^{2}}{k} $
D.此过程物块重力势能增加了 $ mg(H+L)-\dfrac{{m}^{2}{g}^{2}}{k} $
答案:BC
解析:弹簧伸长的长度 $ \mathrm{\Delta }x=\dfrac{mg}{k} $ ,物块上升的高度 $ h=H-L-\mathrm{\Delta }x=H-L-\dfrac{mg}{k} $ ,以地面为零势能面,则物块在空中的重力势能为 $ {E}_{\mathrm{p}1}=mgh=mg(H-L-\dfrac{mg}{k}) $ , $ \mathrm{A} $ 错误;以此时 $ P $ 点所在平面为零势能面,则物块在空中的重力势能为 $ {E}_{\mathrm{p}2}=-mg(L+\mathrm{\Delta }x)=-mg(L+\dfrac{mg}{k}) $ , $ \mathrm{B} $ 正确;以地面为零势能面,此过程中物块重力势能增加量 $ \mathrm{\Delta }{E}_{\mathrm{p}}={E}_{\mathrm{p}1}-0=mg(H-L)-\dfrac{{m}^{2}{g}^{2}}{k} $ , $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
8.如图所示,一只可爱的毛毛虫外出觅食,缓慢经过一边长为 $ \sqrt{3}L $ 的等边三角形障碍物.已知其身长为 $ 3\sqrt{3}L $ ,总质量为 $ m $ ,重力加速度为 $ g $ .如图,其头部刚到达最高点,假设毛毛虫能一直贴着障碍物前行,则从其头部刚到最高点到头部刚到障碍物底端的过程中,毛毛虫的重力势能变化量为( )

A. $ \dfrac{1}{2}mgL $
B. $ \dfrac{1}{4}mgL $
C. $ \dfrac{\sqrt{3}}{2}mgL $
D. $ \dfrac{\sqrt{3}}{4}mgL $
答案:B
解析:选障碍物底端为零势能面,初状态毛毛虫的重力势能为 $ {E}_{1}=\dfrac{1}{3}mg\cdot \dfrac{\sqrt{3}L}{2} \sin {60}^{\circ }=\dfrac{1}{4}mgL $ ,毛毛虫头部越过最高点刚到达障碍物底端时的重力势能为 $ {E}_{2}=\dfrac{2}{3}mg\cdot \dfrac{\sqrt{3}L}{2} \sin {60}^{\circ }=\dfrac{1}{2}mgL $ ,其重力势能的变化量为 $ \mathrm{\Delta }E={E}_{2}-{E}_{1}=\dfrac{1}{4}mgL $ , $ \mathrm{B} $ 正确.
9.关于弹簧的弹性势能,下列说法正确的是( )
A.当弹簧变长时,它的弹性势能一定增大
B.当弹簧变短时,它的弹性势能一定变小
C.在拉伸长度相同时,劲度系数 $ k $ 越大的弹簧,它的弹性势能越大
D.弹性势能是弹簧本身所具有的
答案:C
解析:若弹簧是压缩的,则弹簧变长恢复原长时,它的弹性势能减小,弹簧变短时,它的弹性势能增大, $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;弹性势能与弹簧本身的性质及形变量有关,在拉伸长度相同时,劲度系数 $ k $ 越大的弹簧,它的弹性势能越大, $ \mathrm{C} $ 正确;弹性势能是弹簧和使它发生形变的物体所共有的, $ \mathrm{D} $ 错误.
10.如图是某运动员在撑竿跳比赛过程中的分解动作图,下列说法中正确的是( )
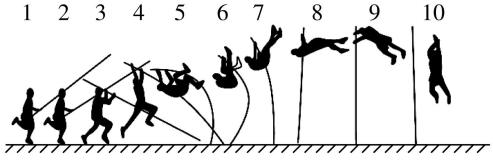
A.从1到3过程中,竿的弹性势能增加
B.从4到7过程中,竿的弹性势能减小
C.从6到8过程中,运动员的重力势能减小
D.从4到9过程中,地面对竿的弹力不做功
答案:D
解析:从1到3过程中,竿一直没有发生形变,弹性势能一直等于 $ {\rm 0,} \mathrm{A} $ 错误;从4到7过程中,竿的形变量先增大后减小,弹性势能先增大后减小, $ \mathrm{B} $ 错误;重力势能 $ {E}_{\mathrm{p}}=mgh $ ,从6到8过程中,运动员距离地面的高度 $ h $ 增大,重力势能增大, $ \mathrm{C} $ 错误;从4到9过程中,地面对竿的弹力作用点的位移等于0,地面对竿的弹力不做功, $ \mathrm{D} $ 正确.
11.如图所示,两光滑直杆 $ OA $ 、 $ OB $ 成 $ {60}^{\circ } $ 角固定在竖直平面内,其角平分线 $ OC $ 竖直.质量均为 $ m $ 的甲、乙两小环套在杆上,用轻质弹簧相连,开始时两环在同一高度且弹簧处于原长状态.将两环同时由静止释放,弹簧始终在弹性限度内,不计空气阻力.在两环沿直杆下滑的过程中,下列说法正确的是( )
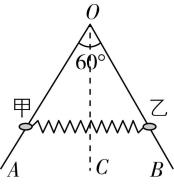
A.两环的加速度一直减小
B.两环的速度先增大后减小
C.两环与杆间的弹力先增大后减小
D.两环的加速度为零时,弹簧的弹性势能最大
答案:B
解析:根据对称性可知,两环在沿直杆下滑的过程中运动情况相同.以甲环为研究对象,在下滑的过程中受到重力、垂直杆向左上的弹力以及弹簧伸长产生的水平向右的弹力.沿杆和垂直杆建立坐标系,沿杆方向,随着甲环的下滑,重力沿杆的分力不变,弹簧弹力沿杆方向的分力不断增大,甲环做加速度减小的加速运动;当弹簧弹力沿杆的分力与重力沿杆的分力大小相等时,甲环加速度为零,速度达到最大;之后甲环继续下滑过程中,弹簧弹力沿杆的分力大于重力沿杆的分力,甲环做加速度增大的减速运动直到速度减小到零,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确.垂直杆方向,重力垂直杆的分力和弹簧弹力垂直杆的分力的合力与杆对环的弹力大小相等,随着环沿杆下滑,弹簧形变量增大,弹簧弹力增大,弹簧弹力垂直杆的分力增大,杆对环的弹力增大,当两环的速度为零时,弹簧的弹性势能最大,故 $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
12.如图所示,将轻弹簧的一端固定,另一端连接一个质量为 $ m $ 、可视为质点的物块,物块在水平桌面上沿 $ x $ 轴运动.以弹簧原长时物块的位置为坐标原点 $ O $ ,当弹簧的伸长量为 $ x $ 时,物块所受弹簧弹力大小为 $ F=kx $ , $ k $ 为常量,图中 $ O{x}_{1}={x}_{1}{x}_{2}={x}_{2}{x}_{3} $ .已知 $ F-x $ 图像中图线与横轴所围面积表示弹力做的功,以下说法正确的是( )
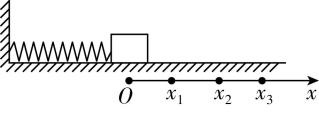
A.物块由 $ O $ 运动到 $ {x}_{1} $ ,弹簧的弹力做正功
B.物块由 $ O $ 向右运动到 $ {x}_{1} $ 与物块由 $ {x}_{1} $ 运动到 $ {x}_{2} $ ,弹簧弹力做功相同
C.物块由 $ {x}_{1} $ 运动到 $ {x}_{2} $ 与由 $ {x}_{2} $ 运动到 $ {x}_{3} $ ,弹簧弹力做功之比为 $ 3:5 $
D.物块由 $ {x}_{1} $ 向右运动到 $ {x}_{2} $ 与物块由 $ {x}_{1} $ 向右运动到 $ {x}_{3} $ 后再返回到 $ {x}_{2} $ ,弹簧弹力做功不相同
答案:C
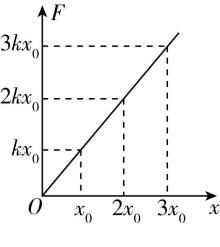
解析:设 $ O{x}_{1}={x}_{1}{x}_{2}={x}_{2}{x}_{3}={x}_{0} $ ,画出弹簧的 $ F-x $ 图像如图所示,物块由 $ O $ 运动到 $ {x}_{1} $ ,弹簧的弹力向左,物块的位移方向向右,弹簧弹力做负功, $ \mathrm{A} $ 错误;物块由 $ O $ 运动到 $ {x}_{1} $ ,弹簧弹力做功大小为 $ {W}_{1}=\dfrac{1}{2}k{x}_{0}^{2} $ ,由 $ {x}_{1} $ 运动到 $ {x}_{2} $ ,弹簧的弹力做功大小为 $ {W}_{2}=\dfrac{k{x}_{0}+2k{x}_{0}}{2}{x}_{0}=\dfrac{3}{2}k{x}_{0}^{2} $ , $ \mathrm{B} $ 错误;物块由 $ {x}_{2} $ 运动到 $ {x}_{3} $ ,弹簧弹力做功大小为 $ {W}_{3}=\dfrac{2k{x}_{0}+3k{x}_{0}}{2}{x}_{0}=\dfrac{5}{2}k{x}_{0}^{2} $ ,则 $ {W}_{2}:{W}_{3}=3:5 $ , $ \mathrm{C} $ 正确;弹簧的弹力做功等于弹性势能的减少量,故物块由 $ {x}_{1} $ 向右运动到 $ {x}_{2} $ 与物块由 $ {x}_{1} $ 向右运动到 $ {x}_{3} $ 后再返回到 $ {x}_{2} $ ,弹簧弹力做的功相同, $ \mathrm{D} $ 错误.
13.如图所示,劲度系数分别为 $ {k}_{A}=400\mathrm{N}/\mathrm{m} $ 和 $ {k}_{B}=600\mathrm{N}/\mathrm{m} $ 的弹簧 $ A $ 和 $ B $ 连接在一起,拉长后将两端固定.弹簧弹性势能可表示为 $ {E}_{\mathrm{p}}=\dfrac{1}{2}k{x}^{2} $ ,其中 $ x $ 为弹簧形变量, $ k $ 为弹簧劲度系数,则弹性势能 $ {E}_{\mathrm{p}A} $ 、 $ {E}_{\mathrm{p}B} $ 的关系为( )
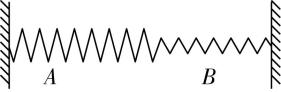
A. $ {E}_{\mathrm{p}A}=\dfrac{3{E}_{\mathrm{p}B}}{2} $
B. $ {E}_{\mathrm{p}A}={E}_{\mathrm{p}B} $
C. $ {E}_{\mathrm{p}A}=\dfrac{2{E}_{\mathrm{p}B}}{3} $
D. $ {E}_{\mathrm{p}A}=\dfrac{{E}_{\mathrm{p}B}}{2} $
答案:A
解析:弹簧 $ A $ 和 $ B $ 两端的拉力大小相等,由胡克定律可知 $ {k}_{A}{x}_{A}={k}_{B}{x}_{B} $ ,解得 $ {x}_{A}:{x}_{B}=3:2 $ ,弹簧 $ A $ 和 $ B $ 的弹性势能分别为 $ {E}_{\mathrm{p}A}=\dfrac{1}{2}{k}_{A}{x}_{A}^{2} $ 、 $ {E}_{\mathrm{p}B}=\dfrac{1}{2}{k}_{B}{x}_{B}^{2} $ ,则 $ \dfrac{{E}_{\mathrm{p}A}}{{E}_{\mathrm{p}B}}=\dfrac{{x}_{A}}{{x}_{B}}=\dfrac{3}{2} $ ,即 $ {E}_{\mathrm{p}A}=\dfrac{3{E}_{\mathrm{p}B}}{2} $ , $ \mathrm{A} $ 正确.




 (多选)
(多选)




