专题10 机车启动的两种方式
一、刷题型
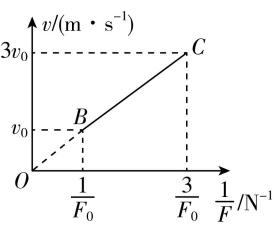
1.某物理小组利用传感器研究某电动车的速度大小 $ v $ 与牵引力大小 $ F $ 的关系,作出 $ v-\dfrac{1}{F} $ 图像,如图所示,电动车最终以大小为 $ 3{v}_{0} $ 的速度做匀速直线运动.电动车的质量为 $ m $ ,运动过程中所受阻力恒定.下列说法正确的是( )
 (多选)
(多选)
A.电动车在 $ BC $ 段的加速度大小不变
B.电动车的功率为 $ 3{F}_{0}{v}_{0} $
C.电动车受到的阻力大小为 $ \dfrac{{F}_{0}}{3} $
D.当电动车的速度大小为 $ {v}_{0} $ 时,其加速度大小为 $ \dfrac{2{F}_{0}}{3m} $
答案:CD
解析:根据 $ P=Fv $ ,可得 $ v=P\dfrac{1}{F} $ , $ v-\dfrac{1}{F} $ 图像的斜率表示功率,根据图像得 $ P=\dfrac{3{v}_{0}-{v}_{0}}{\dfrac{3}{{F}_{0}}-\dfrac{1}{{F}_{0}}}={F}_{0}{v}_{0} $ , $ \mathrm{B} $ 错误;根据牛顿第二定律得 $ F-f=ma $ ,又因为 $ P=Fv $ ,解得 $ \dfrac{P}{v}-f=ma $ ,电动车在 $ BC $ 段速度增大,则加速度减小, $ \mathrm{A} $ 错误;电动车最终以大小为 $ 3{v}_{0} $ 的速度做匀速直线运动,则 $ P=f\cdot 3{v}_{0} $ ,解得 $ f=\dfrac{{F}_{0}}{3} $ , $ \mathrm{C} $ 正确;根据 $ \dfrac{P}{v}-f=ma $ ,当 $ v={v}_{0} $ 时 ,解得 $ a=\dfrac{2{F}_{0}}{3m} $ , $ \mathrm{D} $ 正确.
2.如图所示,配送机器人作为新一代配送工具,可以做到自动规避道路障碍与往来车辆行人,做到自动化配送的全场景适应.该配送机器人机身净质量为 $ 350\mathrm{k}\mathrm{g} $ ,最大承载质量为 $ 200\mathrm{k}\mathrm{g} $ ,在正常行驶中,该配送机器人受到的阻力约为总重力的 $ \dfrac{1}{10} $ ,满载时最大速度可达 $ 5\mathrm{m}/\mathrm{s} $ ,已知重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,关于该机器人的说法正确的是( )

A.该配送机器人的额定功率为 $ 5500\mathrm{W} $
B.该配送机器人以额定功率启动时,先做匀加速运动,后做变加速运动直至达到最大速度
C.该配送机器人空载时,能达到的最大速度为 $ 10\mathrm{m}/\mathrm{s} $
D.满载情况下以额定功率启动,当速度为 $ 2\mathrm{m}/\mathrm{s} $ 时,该配送机器人的加速度大小为 $ 1.5\mathrm{m}/{\mathrm{s}}^{2} $
答案:D
解析:由题意可知配送机器人满载时受到的阻力为 $ f=\dfrac{1}{10}(m+M)g=550\mathrm{N} $ ,满载时最大速度可达 $ 5\mathrm{m}/\mathrm{s} $ ,速度最大时,牵引力与阻力大小相等,则额定功率为 $ P=f{v}_{\mathrm{m}}=2750\mathrm{W} $ ,故 $ \mathrm{A} $ 错误;该配送机器人以额定功率启动时,有 $ P=Fv $ ,随着 $ v $ 增大, $ F $ 逐渐减小,根据牛顿第二定律有 $ F-f=m^\prime a $ ,可知机器人做加速度减小的变加速运动直至达到最大速度,故 $ \mathrm{B} $ 错误;该配送机器人空载时,能达到的最大速度为 $ v^\prime =\dfrac{P}{\dfrac{1}{10}mg}=\dfrac{2750}{350}\mathrm{m}/\mathrm{s}\approx 7.9\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{C} $ 错误;满载情况下以额定功率启动,当速度为 $ 2\mathrm{m}/\mathrm{s} $ 时,牵引力大小为 $ F^\prime =\dfrac{P}{v″}=\dfrac{2750}{2}\mathrm{N}=1375\mathrm{N} $ ,该配送机器人的加速度大小为 $ a=\dfrac{F^\prime -f}{m+M}=\dfrac{1375-550}{550}\mathrm{m}/{\mathrm{s}}^{2}=1.5\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ \mathrm{D} $ 正确.
3.质量为 $ m=2000\mathrm{k}\mathrm{g} $ 的汽车,发动机保持 $ {P}_{0}=60\mathrm{k}\mathrm{W} $ 的功率在平直的公路上行驶,汽车能达到的最大速度为 $ {v}_{\mathrm{m}}=20\mathrm{m}/\mathrm{s} $ .求:
(1) 它以最大速度前进时,所受阻力 $ f $ 的大小;
(2) 若汽车所受阻力大小不变,它的速度为 $ v=10\mathrm{m}/\mathrm{s} $ 时,加速度 $ a $ 的大小.
答案:(1) $ 3000\mathrm{N} $
(2) $ 1.5\mathrm{m}/{\mathrm{s}}^{2} $
解析:(1) 当汽车以最大速度前进时,牵引力与阻力大小相等,则有 $ f=F=\dfrac{{P}_{0}}{{v}_{\mathrm{m}}}=\dfrac{60×{10}^{3}}{20}\mathrm{N}=3000\mathrm{N} $ .
(2) 当汽车的速度为 $ v=10\mathrm{m}/\mathrm{s} $ 时,牵引力大小为 $ {F}_{1}=\dfrac{{P}_{0}}{v}=\dfrac{60×{10}^{3}}{10}\mathrm{N}=6000\mathrm{N} $ ,
根据牛顿第二定律有 $ {F}_{1}-f=ma $ ,
解得 $ a=\dfrac{{F}_{1}-f}{m}=\dfrac{6000-3000}{2000}\mathrm{m}/{\mathrm{s}}^{2}=1.5\mathrm{m}/{\mathrm{s}}^{2} $ .
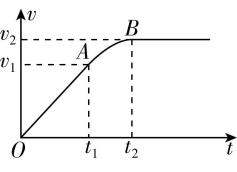
4.一质量为 $ m $ 的汽车在平直路面上匀加速启动, $ {t}_{1} $ 时刻后汽车以额定功率 $ P $ 运动,整个运动过程中汽车的 $ v-t $ 图像如图所示,设汽车所受的阻力恒定,下列分析正确的是( )
 (多选)
(多选)
A.汽车受到的阻力大小为 $ \dfrac{P}{{v}_{1}} $
B. $ 0~{t}_{1} $ 过程中,汽车牵引力的大小为 $ \dfrac{m{v}_{1}}{{t}_{1}}+\dfrac{P}{{v}_{2}} $
C. $ 0~{t}_{2} $ 过程中,汽车牵引力所做的功为 $ P{t}_{2} $
D. $ {t}_{1}~{t}_{2} $ 过程中,汽车牵引力所做的功为 $ P({t}_{2}-{t}_{1}) $
答案:BD
解析: $ {t}_{2} $ 时刻,汽车达到最大速度并开始匀速运动,牵引力大小等于阻力大小,有 $ {F}_{\mathrm{f}}=\dfrac{P}{{v}_{2}} $ , $ \mathrm{A} $ 错误; $ 0~{t}_{1} $ 过程中,汽车做匀加速运动,有 $ F-{F}_{\mathrm{f}}=ma $ , $ a=\dfrac{{v}_{1}}{{t}_{1}} $ ,联立解得牵引力大小 $ F=\dfrac{m{v}_{1}}{{t}_{1}}+\dfrac{P}{{v}_{2}} $ , $ \mathrm{B} $ 正确;汽车在 $ 0~{t}_{1} $ 过程中的功率没有达到额定功率,所以 $ 0~{t}_{2} $ 过程中汽车牵引力所做的功小于 $ P{t}_{2} $ ,
$ \mathrm{C} $ 错误;汽车在 $ {t}_{1}~{t}_{2} $ 过程中的功率为额定功率,所以该过程中汽车牵引力所做的功为 $ P({t}_{2}-{t}_{1}) $ , $ \mathrm{D} $ 正确.
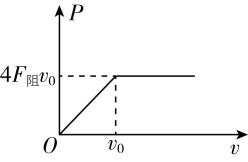
5.一辆质量为 $ m $ (包括人和物品)的赛车在平直的公路上由静止启动,启动过程中赛车的输出功率与速度的关系图像如图所示,运动过程中赛车受到的阻力大小恒为 $ {F}_{阻} $ ,速度达到 $ {v}_{0} $ 后,功率恒为 $ 4{F}_{阻}{v}_{0} $ ,下列说法正确的是( )
 (多选)
(多选)
A.赛车的最大速度为 $ 2{v}_{0} $
B.赛车的最大速度为 $ 4{v}_{0} $
C.赛车做匀加速直线运动的时间为 $ \dfrac{m{v}_{0}}{3{F}_{阻}} $
D.赛车做匀加速直线运动的时间为 $ \dfrac{m{v}_{0}}{4{F}_{阻}} $
答案:BC
解析:赛车的额定功率为 $ P=4{F}_{阻}{v}_{0} $ ,赛车的最大速度为 $ {v}_{\mathrm{m}}=\dfrac{P}{{F}_{阻}}=\dfrac{4{F}_{阻}{v}_{0}}{{F}_{阻}}=4{v}_{0} $ , $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;赛车做匀加速直线运动过程中,牵引力大小为 $ F=\dfrac{P}{{v}_{0}}=4{F}_{阻} $ ,赛车做匀加速直线运动的加速度大小为 $ a=\dfrac{F-{F}_{阻}}{m}=\dfrac{3{F}_{阻}}{m} $ ,赛车做匀加速直线运动的时间为 $ t=\dfrac{{v}_{0}}{a}=\dfrac{m{v}_{0}}{3{F}_{阻}} $ , $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
6.一辆机车在水平轨道上从静止开始做直线运动,其加速度随时间变化的图像如图甲所示,机车牵引力 $ F $ 和车速倒数 $ \dfrac{1}{v} $ 的关系图像如图乙所示,机车前进过程中所受阻力大小恒定, $ t={t}_{0} $ 时刻机车达到额定功率,之后保持该功率不变,下列说法正确的是( )
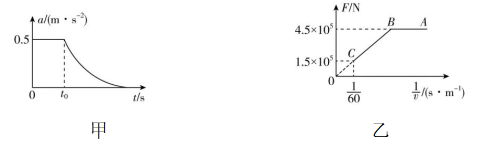 (多选)
(多选)
A.所受恒定阻力大小为 $ 1.5×{10}^{5}\mathrm{N} $
B.机车运动的额定功率为 $ 6×{10}^{6}\mathrm{W} $
C.机车匀加速运动的时间为 $ 40\mathrm{s} $
D.机车的质量为 $ 6×{10}^{5}\mathrm{k}\mathrm{g} $
答案:ACD
解析:由题图乙可知,机车在 $ BC $ 段功率恒定,当速度最大时,机车匀速行驶,机车所受恒定阻力大小等于此时机车牵引力的大小,则有 $ f=F=1.5×{10}^{5}\mathrm{N} $ ,故 $ \mathrm{A} $ 正确;由题图乙可知,机车的最大速度为 $ {v}_{\mathrm{m}}=60\mathrm{m}/\mathrm{s} $ ,机车运动的额定功率 $ P=F{v}_{\mathrm{m}}=f{v}_{\mathrm{m}}=1.5×{10}^{5}×60\mathrm{W}=9×{10}^{6}\mathrm{W} $ ,故 $ \mathrm{B} $ 错误;机车匀加速运动的末速度大小 $ v=\dfrac{P}{{F}_{1}}=\dfrac{9×{10}^{6}}{4.5×{10}^{5}}\mathrm{m}/\mathrm{s}=20\mathrm{m}/\mathrm{s} $ , $ AB $ 段机车匀加速运动,由题图甲可知机车的加速度大小为 $ a=0.5\mathrm{m}/{\mathrm{s}}^{2} $ ,机车匀加速运动的时间 $ {t}_{0}=\dfrac{v}{a}=40\mathrm{s} $ ,故 $ \mathrm{C} $ 正确;机车匀加速运动过程,根据牛顿第二定律,可得 $ {F}_{1}-f=Ma $ ,解得 $ M=6×{10}^{5}\mathrm{k}\mathrm{g} $ ,故 $ \mathrm{D} $ 正确.
7.中国的高铁技术居世界领先地位,通常列车受到的阻力与速度的平方成正比,即 $ f=k{v}^{2} $ .列车要跑得快,必须用大功率的机车牵引.若列车以 $ 120\mathrm{k}\mathrm{m}/\mathrm{h} $ 的速度匀速行驶时机车的功率为 $ P $ ,则该列车以 $ 240\mathrm{k}\mathrm{m}/\mathrm{h} $ 的速度匀速行驶时机车的功率为( )
A. $ 8P $
B. $ 6P $
C. $ 4P $
D. $ 2P $
答案:A
解析:列车匀速行驶时,牵引力与阻力平衡,则有 $ F=f=k{v}^{2} $ ,机车的功率 $ P=Fv=k{v}^{3} $ ,即 $ P\propto {v}^{3} $ ,故列车的速度变为原来的2倍时,功率变为原来的8倍,即 $ P^\prime =8P $ ,故选 $ \mathrm{A} $ .
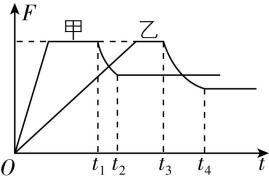
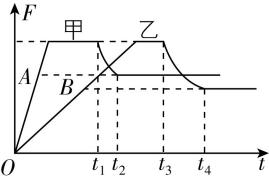
8.额定功率相同的甲、乙两车在同一水平路面上从静止启动,其发动机的牵引力随时间的变化曲线如图所示.两车分别从 $ {t}_{1} $ 和 $ {t}_{3} $ 时刻开始以额定功率行驶,从 $ {t}_{2} $ 和 $ {t}_{4} $ 时刻开始牵引力均视为不变.若两车行驶时所受的阻力大小与重力成正比,且比例系数相同,则( )
 (多选)
(多选)
A.甲车的总重比乙车大
B.甲车比乙车先开始运动
C.甲车在 $ {t}_{1} $ 时刻和乙车在 $ {t}_{3} $ 时刻的速率相同
D.甲车在 $ {t}_{2} $ 时刻和乙车在 $ {t}_{4} $ 时刻的速率相同
答案:ABC
解析:由题意,两车分别从 $ {t}_{1} $ 和 $ {t}_{3} $ 时刻开始以额定功率行驶,从 $ {t}_{2} $ 和 $ {t}_{4} $ 时刻开始牵引力均视为不变,则两辆车 $ {t}_{2} $ 和 $ {t}_{4} $ 时刻开始做匀速直线运动,牵引力大小等于阻力大小,
故可得甲车所受阻力大于乙车所受阻力,根据 $ F=f=kmg $ ,可知甲车的总重比乙车大, $ \mathrm{A} $ 正确;如图所示,甲车在 $ A $ 点所对应的时刻牵引力与阻力大小相等,所以甲车从这个时刻开始运动,乙车在 $ B $ 点所对应的时刻牵引力与阻力大小相等,乙车从这个时刻开始运动,所以甲车比乙车先开始运动, $ \mathrm{B} $ 正确;两车分别从 $ {t}_{1} $ 和 $ {t}_{3} $ 时刻开始以额定功率行驶,这两个时刻,两车的牵引力等大,又两车额定功率 $ P $ 相同,由 $ P=Fv $ 可知,甲车在 $ {t}_{1} $ 时刻和乙车在 $ {t}_{3} $ 时刻的速率相同, $ \mathrm{C} $ 正确;由前面分析知,两车在 $ {t}_{2} $ 和 $ {t}_{4} $ 时刻开始做匀速直线运动,牵引力大小等于阻力大小,则 $ {t}_{2} $ 时刻甲车达到最大速度, $ {t}_{4} $ 时刻乙车达到最大速度,由于甲车的牵引力比乙车大,根据 $ P=Fv $ 可知甲车在 $ {t}_{2} $ 时刻的速率小于乙车在 $ {t}_{4} $ 时刻的速率, $ \mathrm{D} $ 错误.
9.一辆洒水车空载时的质量为 $ M $ ,满载时水的质量为 $ {m}_{0} $ ,正常工作时每秒钟向外洒水的质量为 $ m $ ,洒水车一直在平直路面上行驶,且洒水车在平直路面上受到的阻力等于其总重力的 $ k $ 倍,洒水车发动机的额定功率为 $ {P}_{0} $ ,重力加速度为 $ g $ .
(1) 求洒水车满载时的最大速度 $ {v}_{\mathrm{m}} $ ;
(2) 若洒水车始终以速度 $ v $ 做匀速直线运动,某时刻从满载状态开始正常工作,求洒水车从此时刻起向前运动 $ s $ 的距离(水未洒完)时的牵引力大小(该过程中洒水车发动机的功率未达到额定功率);
(3) 若洒水车由静止开始做加速度大小为 $ a $ 的匀加速直线运动,启动时从满载状态开始正常工作,整个过程水始终未洒完,求洒水车发动机的最大功率(该过程中洒水车发动机的功率未达到额定功率).
答案:(1) $ \dfrac{{P}_{0}}{k(M+{m}_{0})g} $
(2) $ k(M+{m}_{0}-m\dfrac{s}{v})g $
(3) $ \dfrac{a (a+kg ) (M+{m}_{0})^{2}}{4m} $
解析:(1) 洒水车满载时,所受阻力 $ f=k(M+{m}_{0})g $ ,达到最大速度时,牵引力与阻力大小相等,则 $ {v}_{\mathrm{m}}=\dfrac{{P}_{0}}{F}=\dfrac{{P}_{0}}{f} $ ,解得 $ {v}_{\mathrm{m}}=\dfrac{{P}_{0}}{k(M+{m}_{0})g} $ .
(2) 洒水车匀速向前运动 $ s $ 的距离,所经历的时间 $ t^\prime =\dfrac{s}{v} $ ,
洒水车向外洒出的水的质量为 $ mt\prime $ ,此时洒水车所受阻力 $ f^\prime =k(M+{m}_{0}-mt\prime )g $ ,洒水车匀速运动,牵引力与阻力大小相等,有 $ F^\prime =f^\prime $ ,解得 $ F^\prime =k(M+{m}_{0}-m\dfrac{s}{v})g $ .
(3) 设发动机的功率为 $ P $ ,经一段时间 $ t $ 后的速度大小为 $ v^\prime $ ,根据匀变速直线运动的规律有 $ v^\prime =at $ ,此时发动机牵引力大小为 $ F=\dfrac{P}{v^\prime } $ ,根据牛顿第二定律得 $ F-f=(M+{m}_{0}-mt)a $ ,阻力与时间的关系为 $ f=k(M+{m}_{0}-mt)g $ ,
联立可得 $ P=a(a+kg)[(M+{m}_{0})t-m{t}^{2}] $ ,
由数学知识可得,当 $ t=\dfrac{M+{m}_{0}}{2m} $ 时功率有最大值,最大值为 $ {P}_{ \max }=\dfrac{a (a+kg ) (M+{m}_{0})^{2}}{4m} $ .
 (多选)
(多选)
 (多选)
(多选) (多选)
(多选)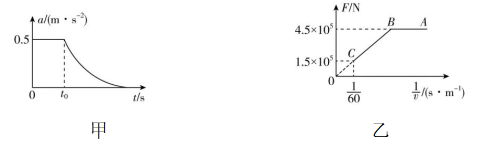 (多选)
(多选) (多选)
(多选)