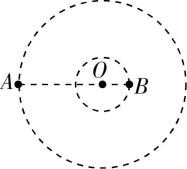
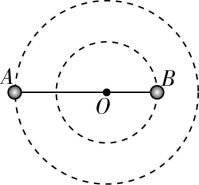
8.天文学家观测河外星系大麦哲伦云时,发现了 $ \mathrm{L}\mathrm{M}\mathrm{C}\mathrm{X}-3 $ 双星系统,它由可见星 $ A $ 和不可见的暗星 $ B $ 构成,将两星视为质点,不考虑其他天体的影响 $ {\rm .} A $ 、 $ B $ 围绕两者连线上的 $ O $ 点做匀速圆周运动,它们之间的距离保持不变,如图所示.可见星 $ A $ 所受暗星 $ B $ 的引力 $ {F}_{A} $ 可等效为位于 $ O $ 点处质量为 $ m^\prime $ 的星体(视为质点)对它的引力,引力常量为 $ G $ ,由观测能够得到可见星 $ A $ 的速率 $ v $ 和运行周期 $ T $ .
(1) 设 $ A $ 和 $ B $ 的质量分别为 $ {m}_{1} $ 、 $ {m}_{2} $ ,试求 $ m^\prime $ 的表达式(用 $ {m}_{1} $ 、 $ {m}_{2} $ 表示);
(2) 求暗星 $ B $ 的质量 $ {m}_{2} $ 与可见星 $ A $ 的速率 $ v $ 、运行周期 $ T $ 和质量 $ {m}_{1} $ 之间的关系式;
(3) 恒星演化到末期,如果其质量大于太阳质量 $ {m}_{\mathrm{S}} $ 的2倍,它将有可能成为黑洞.若可见星 $ A $ 的速率 $ v=2.7×{10}^{5}\mathrm{m}/\mathrm{s} $ ,运行周期 $ T=4.7\mathrm{\pi }×{10}^{4}\mathrm{s} $ ,质量 $ {m}_{1}=6{m}_{\mathrm{S}} $ ,试通过估算来判断暗星 $ B $ 有可能是黑洞吗? $ (G=6.67×{10}^{-11}\mathrm{N}\cdot {\mathrm{m}}^{2}/{\mathrm{k}\mathrm{g}}^{2},{m}_{\mathrm{S}}=2.0×{10}^{30}\mathrm{k}\mathrm{g}) $
解析:(1) 设 $ A $ 、 $ B $ 的轨道半径分别为 $ {r}_{1} $ 、 $ {r}_{2} $ ,由题意知, $ A $ 、 $ B $ 做匀速圆周运动的角速度相同,设为 $ \omega $ ,有 $ {F}_{A}={m}_{1}{\omega }^{2}{r}_{1} $ , $ {F}_{B}={m}_{2}{\omega }^{2}{r}_{2} $ ,且 $ {F}_{A}={F}_{B} $ ,
设 $ A $ 、 $ B $ 之间的距离为 $ r $ ,有 $ r={r}_{1}+{r}_{2} $ ,联立解得 $ r=\dfrac{{m}_{1}+{m}_{2}}{{m}_{2}}{r}_{1} $ ,由万有引力定律有 $ {F}_{A}=G\dfrac{{m}_{1}{m}_{2}}{{r}^{2}} $ ,可得 $ {F}_{A}=G\dfrac{{m}_{1}{m}_{2}^{3}}{{\left({m}_{1}+{m}_{2}\right) ^ {2}}{r}_{1}^{2}} $ ,又 $ {F}_{A}=G\dfrac{{m}_{1}m^\prime }{{r}_{1}^{2}} $ ,比较可得 $ m^\prime =\dfrac{{m}_{2}^{3}}{{\left({m}_{1}+{m}_{2}\right) ^ {2}}} $ .
(2) 对星 $ A $ ,由牛顿第二定律,有 $ G\dfrac{{m}_{1}m^\prime }{{r}_{1}^{2}}={m}_{1}\frac{{v}^{2}}{{r}_{1}} $ ,星 $ A $ 的轨道半径 $ {r}_{1}=\dfrac{vT}{2\mathrm{\pi }} $ ,联立可得 $ \dfrac{{m}_{2}^{3}}{{\left({m}_{1}+{m}_{2}\right) ^ {2}}}=\dfrac{{v}^{3}T}{2\mathrm{\pi }G} $ .
(3) 将 $ {m}_{1}=6{m}_{\mathrm{S}} $ 代入(2)中的关系式可得 $ \dfrac{{m}_{2}^{3}}{{\left(6{m}_{\mathrm{S}}+{m}_{2}\right) ^ {2}}}=\dfrac{{v}^{3}T}{2\mathrm{\pi }G} $ ,
代入数据得 $ \dfrac{{m}_{2}^{3}}{{\left(6{m}_{\mathrm{S}}+{m}_{2}\right) ^ {2}}}=6.9×{10}^{30}\mathrm{k}\mathrm{g}=3.45{m}_{\mathrm{S}} $ ,
设 $ {m}_{2}=n{m}_{\mathrm{S}}(n > 0) $ ,则 $ \dfrac{{m}_{2}^{3}}{{\left(6{m}_{\mathrm{S}}+{m}_{2}\right) ^ {2}}}=\dfrac{n}{{\left(\dfrac{6}{n}+1\right) ^ {2}}}{m}_{\mathrm{S}} $ ,
可见, $ \dfrac{{m}_{2}^{3}}{{\left(6{m}_{\mathrm{S}}+{m}_{2}\right) ^ {2}}} $ 的值随 $ n $ 的增大而增大,令 $ n=2 $ ,
得 $ \dfrac{n}{{\left(\dfrac{6}{n}+1\right) ^ {2}}}{m}_{\mathrm{S}}=0.125{m}_{\mathrm{S}} < 3.45{m}_{\mathrm{S}} $ ,
若使上式成立,则 $ n $ 必大于2,即暗星 $ B $ 的质量 $ {m}_{2} $ 必大于 $ 2{m}_{\mathrm{S}} $ ,由此可判断暗星 $ B $ 有可能是黑洞.