第2节 万有引力定律
一、刷基础
1.在万有引力定律得出的过程中,物理学家进行了著名的“月—地”检测.已知月心到地心的距离 $ r $ 、月球的公转周期 $ T $ ,地球的半径 $ R $ 、质量 $ M $ ,地球表面的重力加速度 $ g $ ,地面上物体所受重力为 $ {F}_{1} $ ,地球吸引月球的力为 $ {F}_{2} $ .则( )(多选)
A.“月—地”检测的目的是验证 $ {F}_{1} $ 、 $ {F}_{2} $ 是同一性质的力
B.“月—地”检测的目的是测定引力常量 $ G $
C.用 $ r $ 、 $ R $ 、 $ M $ 和 $ g $ 正确推导就能完成“月—地”检测
D.用 $ r $ 、 $ R $ 、 $ T $ 和 $ g $ 正确推导就能完成“月—地”检测
答案:AD
解析:“月—地”检测的目的是验证地球对月球的引力与地球对地面物体的引力为同一种性质的力,并验证这种力是否遵循距离平方反比规律,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;对月球有 $ G\dfrac{M{m}_{月}}{{r}^{2}}={m}_{月}\frac{4{\mathrm{\pi }}^{2}r}{{T}^{2}} $ ,对地面上的物体有 $ G\dfrac{Mm\prime }{{R}^{2}}=m^\prime g $ ,若计算得到 $ \dfrac{{R}^{2}}{{r}^{2}}=\dfrac{\dfrac{4{\mathrm{\pi }}^{2}r}{{T}^{2}}}{g} $ ,就可以完成“月—地”检测,因此需要用到的物理量是 $ r $ 、 $ R $ 、 $ T $ 和 $ g $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
2.下列关于万有引力定律的说法正确的是( )
A.牛顿发现了万有引力定律,卡文迪什测得了引力常量
B.两物体间的万有引力总是大小相等、方向相反,是一对平衡力
C.根据表达式 $ F=G\dfrac{{m}_{1}{m}_{2}}{{r}^{2}} $ 可知,当 $ r $ 趋近于零时,万有引力趋近于无穷大
D.根据表达式 $ F=G\dfrac{{m}_{1}{m}_{2}}{{r}^{2}} $ 得 $ G=\dfrac{F{r}^{2}}{{m}_{1}{m}_{2}} $ ,由此可知引力常量 $ G $ 与 $ F $ 、 $ r $ 、 $ {m}_{1} $ 、 $ {m}_{2} $ 有关
答案:A
解析:牛顿发现了万有引力定律,卡文迪什通过扭秤实验测定了引力常量,故 $ \mathrm{A} $ 正确;万有引力是两物体间的相互作用力,大小相等、方向相反,作用在不同物体上,属于作用力与反作用力,故 $ \mathrm{B} $ 错误;万有引力公式 $ F=G\dfrac{{m}_{1}{m}_{2}}{{r}^{2}} $ 仅适用于质点或均匀球体间的计算,当 $ r $ 趋近于零时,物体无法视为质点,此公式不适用,故 $ \mathrm{C} $ 错误;引力常量 $ G $ 是普适常数,与 $ F $ 、 $ r $ 、 $ {m}_{1} $ 、 $ {m}_{2} $ 无关, $ G=\dfrac{F{r}^{2}}{{m}_{1}{m}_{2}} $ 仅用于计算 $ G $ 的数值,故 $ \mathrm{D} $ 错误.
3.1687年牛顿提出万有引力定律,根据该定律,要使两质点间的万有引力减小到原来的 $ \dfrac{1}{16} $ ,下列说法正确的是( )(多选)
A.使两质点的质量各减小一半,距离变为原来的2倍
B.使两质点的质量和两质点间的距离都减小到原来的 $ \dfrac{1}{2} $
C.使其中一个质点的质量减小到原来的 $ \dfrac{1}{4} $ ,距离变为原来的2倍
D.使两质点间的距离增大到原来的4倍,质量均变为原来的2倍
答案:AC
解析:根据 $ F=G\dfrac{{m}_{1}{m}_{2}}{{r}^{2}} $ 可知,使两质点的质量各减小一半,距离变为原来的2倍,则两质点间的万有引力减小到原来的 $ \dfrac{1}{16} $ ,故 $ \mathrm{A} $ 正确;使两质点的质量和两质点间的距离都减小到原来的 $ \dfrac{1}{2} $ ,则两质点间的万有引力大小不变,故 $ \mathrm{B} $ 错误;使其中一个质点的质量减小到原来的 $ \dfrac{1}{4} $ ,距离变为原来的2倍,则两质点间的万有引力减小到原来的 $ \dfrac{1}{16} $ ,故 $ \mathrm{C} $ 正确;使两质点间的距离增大到原来的4倍,质量均变为原来的2倍,则两质点间的万有引力减小到原来的 $ \dfrac{1}{4} $ ,故 $ \mathrm{D} $ 错误.
4.已知火星质量为地球质量的 $ k $ 倍,其半径为地球半径的 $ p $ 倍,由此可知同一物体在火星表面与在地球表面受到的引力的比值为( )
A. $ \dfrac{k}{p} $
B. $ \dfrac{k}{{p}^{2}} $
C. $ \dfrac{{k}^{2}}{p} $
D. $ \dfrac{{k}^{2}}{{p}^{2}} $
答案:B
解析:设物体的质量为 $ m $ ,则物体在地球表面受到的引力为 $ F=G\dfrac{Mm}{{r}^{2}} $ ,同理在火星表面,物体受到的引力为 $ F^\prime =G\dfrac{M^\prime m}{r{\prime }^{2}} $ ,又因为火星质量为地球质量的 $ k $ 倍,其半径为地球半径的 $ p $ 倍,联立得同一物体在火星表面与在地球表面受到的引力的比值为 $ \dfrac{F^\prime }{F}=\dfrac{k}{{p}^{2}} $ , $ \mathrm{B} $ 正确.
5.如图所示,在一半径为 $ R $ 、质量分布均匀的大球内部挖去一半径为 $ \dfrac{R}{2} $ 的小球,两球相切于 $ P $ 点, $ {O}_{1} $ 、 $ {O}_{2} $ 分别是大球和小球的球心.已知质量分布均匀的球壳对球壳内部物体的万有引力为零,大球密度为 $ \rho $ ,引力常量为 $ G $ .现将一质量为 $ m $ 的物体 $ N $ (可视为质点)置于 $ {O}_{1} $ 处,则大球剩余部分对物体 $ N $ 的万有引力大小为( )
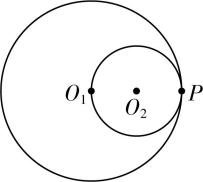
A. $ \dfrac{1}{3}\mathrm{\pi }\rho GmR $
B. $ \dfrac{2}{3}\mathrm{\pi }\rho GmR $
C. $ \mathrm{\pi }\rho GmR $
D. $ \dfrac{4}{3}\mathrm{\pi }\rho GmR $
答案:B
解析:物体 $ N $ 受到的大球剩余部分的引力为完整大球对物体 $ N $ 的引力减去小球对物体 $ N $ 的引力,未挖去小球前,大球对物体 $ N $ 的引力为零,所以大球剩余部分对物体 $ N $ 的引力大小等于小球对物体 $ N $ 的引力大小,根据万有引力定律可得 $ F=G\dfrac{m^\prime m}{{\left(\dfrac{R}{2}\right) ^ {2}}} $ , $ m^\prime =\rho \cdot \dfrac{4}{3}\mathrm{\pi }{\left(\dfrac{R}{2}\right) ^ {3}} $ ,联立可得 $ F=\dfrac{2}{3}\mathrm{\pi }\rho GmR $ ,故 $ \mathrm{B} $ 正确.
6.嫦娥六号探测器曾实施月面“挖土”,“挖土”采用了钻取和表取两种模式.假设月球可看作质量分布均匀的球体,其质量为 $ M $ ,半径为 $ R $ .已知质量分布均匀的球壳对壳内物体的万有引力为零,引力常量为 $ G $ ,忽略月球自转.某次钻取中质量为 $ m $ 的钻尖进入月球表面以下 $ h $ 深处,则此时月球对钻尖的万有引力大小为( )
A.0
B. $ G\dfrac{Mm}{{R}^{2}} $
C. $ G\dfrac{Mm}{(R-h)R} $
D. $ G\dfrac{(R-h)Mm}{{R}^{3}} $
答案:D
解析:设月球密度为 $ \rho $ ,则月球质量 $ M=\rho \cdot \dfrac{4}{3}\mathrm{\pi }{R}^{3} $ ,半径为 $ R-h $ 的球体质量为 $ M^\prime =\rho \cdot \dfrac{4}{3}\mathrm{\pi }(R-h)^{3} $ ,已知质量分布均匀的球壳对壳内物体的万有引力为零,则质量为 $ m $ 的钻尖进入月球表面以下 $ h $ 深处受到的万有引力大小 $ F=\dfrac{GM\prime m}{ (R-h)^{2}}=G\dfrac{ (R-h )Mm}{{R}^{3}} $ ,故 $ \mathrm{D} $ 正确.
二、刷提升
1.卡文迪什巧妙地利用扭秤装置,第一次在实验室里比较准确地测出了引力常量 $ G $ ,用国际单位制的基本单位表示引力常量 $ G $ 的单位是( )
A. $ {\mathrm{m}}^{2}\cdot {\mathrm{k}\mathrm{g}}^{-1}\cdot {\mathrm{s}}^{-2} $
B. $ {\mathrm{m}}^{3}\cdot {\mathrm{k}\mathrm{g}}^{-1}\cdot {\mathrm{s}}^{-2} $
C. $ {\mathrm{m}}^{2}\cdot {\mathrm{k}\mathrm{g}}^{-2}\cdot {\mathrm{s}}^{-2} $
D. $ {\mathrm{m}}^{3}\cdot {\mathrm{k}\mathrm{g}}^{-2}\cdot {\mathrm{s}}^{-2} $
答案:B
解析:根据万有引力定律 $ F=G\dfrac{{m}_{1}{m}_{2}}{{r}^{2}} $ ,可得 $ G=\dfrac{F{r}^{2}}{{m}_{1}{m}_{2}} $ ,所以 $ G $ 的单位为 $ \dfrac{\mathrm{k}\mathrm{g}\cdot \mathrm{m}\cdot {\mathrm{s}}^{-2}\cdot {\mathrm{m}}^{2}}{{\mathrm{k}\mathrm{g}}^{2}}={\mathrm{m}}^{3}\cdot {\mathrm{k}\mathrm{g}}^{-1}\cdot {\mathrm{s}}^{-2} $ ,故 $ \mathrm{B} $ 正确.
2.如图所示,三个质量均为 $ M $ 的球分别位于 $ \dfrac{3}{4} $ 圆环、半圆环和完整圆环的圆心, $ \dfrac{3}{4} $ 圆环、半圆环分别是由与丙图中相同的完整圆环截去 $ \dfrac{1}{4} $ 和一半所得,环的粗细忽略不计,若甲图中 $ \dfrac{3}{4} $ 圆环对球的引力大小为 $ F $ ,则乙图中半圆环、丙图中圆环对球的引力大小分别为( )
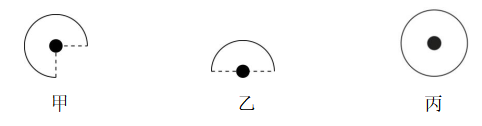
A. $ \sqrt{2}F $ , $ 2\sqrt{2}F $
B. $ \sqrt{2}F {\rm ,0} $
C. $ \dfrac{3}{2}F {\rm ,0} $
D. $ \dfrac{2}{3}F $ , $ \dfrac{4}{3}F $
答案:B
解析:将题图甲中的 $ \dfrac{3}{4} $ 圆环分成3个 $ \dfrac{1}{4} $ 圆环,则由对称性可知, $ \dfrac{3}{4} $ 圆环对球的引力大小等于其中的一个 $ \dfrac{1}{4} $ 圆环对球的引力大小,则每个 $ \dfrac{1}{4} $ 圆环对球的引力大小均为 $ F $ ,则题图乙中半圆环对球的引力大小为 $ {F}_{乙}=\sqrt{{F}^{2}+{F}^{2}}=\sqrt{2}F $ ,题图丙中由对称性可知,整个圆环对球的引力为零, $ \mathrm{B} $ 正确.
3.人造地球卫星 $ B $ 的质量是 $ A $ 的4倍,某时刻, $ A $ 、 $ B $ 同时位于各自椭圆轨道的近地点(此时不算 $ A $ 、 $ B $ 第一次经过近地点),此时 $ A $ 、 $ B $ 所受到地球的万有引力大小相等.此后当 $ A $ 第四次经过其轨道的近地点时, $ B $ 恰好第一次经过其轨道的远地点.已知 $ A $ 的近、远地点到地球球心的距离分别为 $ r $ 和 $ 3r $ ,则 $ B $ 的远地点到地球球心的距离为( )
A. $ 7r $
B. $ 8r $
C. $ 14r $
D. $ 16r $
答案:C
解析: $ A $ 、 $ B $ 同时位于各自椭圆轨道的近地点时, $ A $ 、 $ B $ 所受到地球的万有引力大小相等,设 $ B $ 的近地点距离地心的距离为 $ x $ ,则有 $ G\dfrac{Mm}{{r}^{2}}=G\dfrac{M\cdot 4m}{{x}^{2}} $ ,又知 $ A $ 第四次经过其轨道的近地点时, $ B $ 恰好第一次经过其轨道的远地点,则 $ 4{T}_{A}=\dfrac{1}{2}{T}_{B} $ ,设 $ B $ 的远地点距离地心的距离为 $ y $ ,由开普勒第三定律得 $ \dfrac{{T}_{A}^{2}}{{T}_{B}^{2}}=\dfrac{{\left(\dfrac{r+3r}{2}\right) ^ {3}}}{{\left(\dfrac{x+y}{2}\right) ^ {3}}} $ ,联立解得 $ x=2r $ , $ y=14r $ , $ \mathrm{C} $ 正确.
4.如图甲所示,质量分布均匀的球壳,对其内部任意一点的万有引力为零.如图乙所示,将地球视为质量分布均匀的球体,从地表往地心挖一条很窄的矿井,从井口静止释放一物块.忽略一切摩擦和地球的自转,从地表到地心,物块的速度—时间图像和加速度—时间图像大致正确的是( )

A.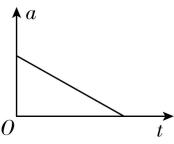
B.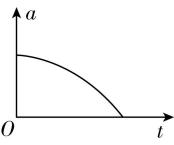
C.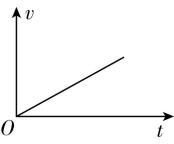
D.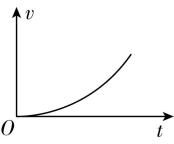
答案:B
解析:设地球的密度为 $ \rho $ ,当物块距地心的距离为 $ x $ 时,受到的万有引力为 $ F=G\dfrac{Mm}{{x}^{2}} $ ,其中 $ M=\rho \cdot \dfrac{4}{3}\mathrm{\pi }{x}^{3} $ ,解得 $ F=\dfrac{4\mathrm{\pi }\rho Gxm}{3} $ .根据牛顿第二定律,可得加速度为 $ a=\dfrac{F}{m}=\dfrac{4\mathrm{\pi }\rho G}{3}x $ ,因为 $ x $ 越来越小,所以加速度 $ a $ 越来越小 $ {\rm .} a-t $ 图像的切线斜率 $ \dfrac{\mathrm{\Delta }a}{\mathrm{\Delta }t}=\dfrac{4\mathrm{\pi }\rho G}{3}\cdot \dfrac{\mathrm{\Delta }x}{\mathrm{\Delta }t}=\dfrac{4\mathrm{\pi }\rho G}{3}v $ ,因为物块向地心下落,速率越来越大,故 $ a-t $ 图像切线的斜率的绝对值增大,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;速度—时间图像的斜率表示加速度,由以上分析可知,加速度越来越小,故 $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
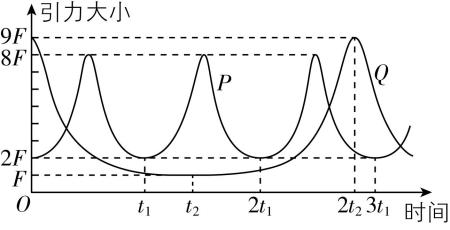
5.卫星 $ P $ 、 $ Q $ 绕某行星运动的轨道均为椭圆,只考虑 $ P $ 、 $ Q $ 受到该行星的引力,引力大小随时间的变化如图所示,已知 $ {t}_{2}=\sqrt{2}{t}_{1} $ ,下列说法正确的是( )
 (多选)
(多选)
A. $ P $ 、 $ Q $ 绕行星公转的周期之比为 $ 1:2\sqrt{2} $
B. $ P $ 、 $ Q $ 到行星中心距离的最小值之比为 $ 3:2 $
C. $ P $ 、 $ Q $ 的质量之比为 $ 32:81 $
D. $ P $ 、 $ Q $ 的质量之比为 $ 81:32 $
答案:AC
解析:由题图可知 $ {T}_{1}:{T}_{2}={t}_{1}:2{t}_{2}=1:2\sqrt{2} $ ,故 $ \mathrm{A} $ 正确;当 $ P $ 离行星最近时有 $ 8F=G\dfrac{M{m}_{1}}{{d}_{1}^{2}} $ ,当 $ P $ 离行星最远时有 $ 2F=G\dfrac{M{m}_{1}}{{d}_{2}^{2}} $ ;当 $ Q $ 离行星最近时有 $ 9F=G\dfrac{M{m}_{2}}{{l}_{1}^{2}} $ ,当 $ Q $ 离行星最远时有 $ F=G\dfrac{M{m}_{2}}{{l}_{2}^{2}} $ ,由开普勒第三定律可知 $ {\left(\dfrac{{T}_{1}}{{T}_{2}}\right) ^ {2}}={\left(\dfrac{\dfrac{{d}_{1}+{d}_{2}}{2}}{\dfrac{{l}_{1}+{l}_{2}}{2}}\right) ^ {3}} $ ,联立解得 $ {d}_{1}:{l}_{1}=2:3 $ ,故 $ \mathrm{B} $ 错误;由前面分析可知 $ \dfrac{8F}{9F}=\dfrac{G\dfrac{M{m}_{1}}{{d}_{1}^{2}}}{G\dfrac{M{m}_{2}}{{l}_{1}^{2}}} $ ,解得 $ {m}_{1}:{m}_{2}=32:81 $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.







 (多选)
(多选)