1.关于开普勒第三定律 $ \dfrac{{a}^{3}}{{T}^{2}}=k $ 中的 $ k $ ,下列说法正确的是( )
A. $ k $ 与 $ T $ 、 $ a $ 均无关
B. $ k $ 随 $ a $ 的增大而增大
C. $ k $ 随 $ T $ 的减小而增大
D.对于地球绕太阳运动和月球绕地球运动, $ k $ 相同
答案:A
解析:根据开普勒第三定律可知, $ k $ 与轨道半长轴 $ a $ 和周期 $ T $ 无关,仅取决于中心天体的质量,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误;地球绕太阳运动和月球绕地球运动的中心天体不同, $ k $ 不同,故 $ \mathrm{D} $ 错误.
2.如图所示,八大行星沿椭圆轨道绕太阳公转,下列说法中正确的是( )
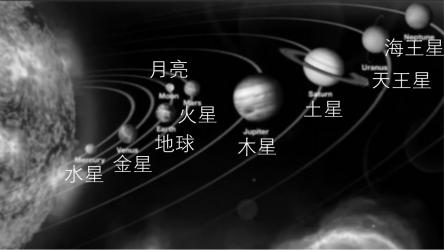
A.土星的公转周期比地球的小
B.火星绕太阳运行过程中,速率不变
C.太阳处在八大行星的椭圆轨道的一个公共焦点上
D.地球和土星分别与太阳的连线在相同时间内扫过的面积相等
答案:C
解析:由开普勒第三定律 $ \dfrac{{a}^{3}}{{T}^{2}}=k $ 可知,土星的轨道半长轴大于地球的轨道半长轴,则土星的公转周期比地球的大, $ \mathrm{A} $ 错误;火星绕太阳的运行轨道为椭圆,运行过程中,速率发生变化, $ \mathrm{B} $ 错误;由开普勒第一定律可知,太阳处在八大行星的椭圆轨道的一个公共焦点上, $ \mathrm{C} $ 正确;由开普勒第二定律可知,同一行星与太阳的连线在相同时间内扫过的面积相等,但地球和土星分别与太阳的连线在相同时间内扫过的面积不相等, $ \mathrm{D} $ 错误.
3.欧洲航天局在2025年2月4日宣布,欧洲航天局利用空间探测器探测到一颗巨大的系外行星盖亚 $ -4\mathrm{b} $ ,环绕着一恒星公转,其椭圆轨道如图所示,环绕周期大约为570天.连线 $ ac $ 为长轴,连线 $ bd $ 为短轴,其环绕方向为顺时针.下列说法正确的是( )
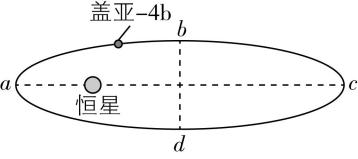
A.盖亚 $ -4\mathrm{b} $ 在 $ b $ 、 $ d $ 两点的加速度相同
B.盖亚 $ -4\mathrm{b} $ 在 $ a $ 点的速率小于在 $ c $ 点的速率
C.盖亚 $ -4\mathrm{b} $ 从 $ b $ 经 $ c $ 到 $ d $ 的时间大于285天
D.恒星不一定处在椭圆的焦点上
答案:C
解析:根据对称性可知,盖亚 $ -4\mathrm{b} $ 在 $ b $ 、 $ d $ 两点的加速度大小相等,方向不同,故 $ \mathrm{A} $ 错误;由于 $ a $ 点是椭圆轨道的近恒星点, $ c $ 点是椭圆轨道的远恒星点,根据开普勒第二定律可知,盖亚 $ -4\mathrm{b} $ 在 $ a $ 点的速率大于在 $ c $ 点的速率,故 $ \mathrm{B} $ 错误;由于从 $ a $ 点到 $ b $ 点再到 $ c $ 点,盖亚 $ -4\mathrm{b} $ 的速率减小,则盖亚 $ -4\mathrm{b} $ 从 $ b $ 经 $ c $ 到 $ d $ 的时间大于环绕周期的一半,即大于285天,故 $ \mathrm{C} $ 正确;根据开普勒第一定律可知,恒星一定处在椭圆的焦点上,故 $ \mathrm{D} $ 错误.
4.阋神星是一个已知质量最大的属于柯伊伯带及海王星外天体的矮行星.若将地球和阋神星绕太阳的运动看作匀速圆周运动,它们的运行轨道如图所示.已知阋神星绕太阳运行一周的时间约为 $ n $ 年,设地球绕太阳运行的轨道半径为 $ R $ ,则阋神星绕太阳运行的轨道半径约为( )
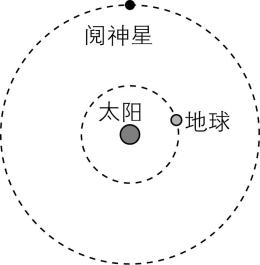
A. $ \sqrt[3]{n}R $
B. $ \sqrt{n}R $
C. $ \sqrt[3]{{n}^{2}}R $
D. $ \sqrt{{n}^{3}}R $
答案:C
解析:依题意,由开普勒第三定律可得 $ \dfrac{{R}_{地}^{3}}{{T}_{地}^{2}}=\dfrac{{R}_{阋}^{3}}{{T}_{阋}^{2}} $ ,其中 $ {T}_{阋}=n{T}_{地} $ , $ {R}_{地}=R $ ,解得阋神星绕太阳运行的轨道半径为 $ {R}_{阋}=\sqrt[3]{{n}^{2}}R $ ,故选 $ \mathrm{C} $ .
5.地球赤道上空有一颗运动方向与地球自转方向相反的卫星 $ A $ ,卫星 $ A $ 对地球的最大张角 $ \theta ={90}^{\circ } $ .赤道上有一个信号接收中心,可以在不被地球遮挡的情况下接收来自卫星的信号.已知地球近地卫星的周期约为 $ 1.4\mathrm{h} $ ,则该接收中心能够连续接收到卫星 $ A $ 信号的最长时间接近 $ (\sqrt{2\sqrt{2}}\approx 1.7) $ ( )
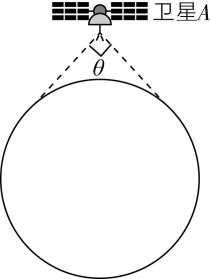
A. $ 0.35\mathrm{h} $
B. $ 0.55\mathrm{h} $
C. $ 0.75\mathrm{h} $
D. $ 0.95\mathrm{h} $
答案:B
解析:设地球半径为 $ R $ ,由几何关系可知卫星 $ A $ 的轨迹半径为 $ r=\dfrac{R}{ \sin {45}^{\circ }}=\sqrt{2}R $ ,设卫星 $ A $ 的周期为 $ {T}_{A} $ ,根据开普勒第三定律可得 $ \dfrac{{r}^{3}}{{R}^{3}}=\dfrac{{T}_{A}^{2}}{{T}_{近}^{2}} $ ,解得 $ {T}_{A}=2.38\mathrm{h} $ ,设接收中心能连续接收到卫星 $ A $ 信号的最长时间为 $ t $ ,由几何关系可得 $ (\dfrac{2\mathrm{\pi }}{{T}_{A}}+\dfrac{2\mathrm{\pi }}{{T}_{自}})t=\dfrac{\mathrm{\pi }}{2} $ ,其中 $ {T}_{自}=24\mathrm{h} $ ,解得 $ t\approx 0.54\mathrm{h} $ ,该接收中心能够连续接收到卫星 $ A $ 信号的最长时间接近 $ 0.55\mathrm{h} $ ,故选 $ \mathrm{B} $ .



