第六章素养检测
一、刷速度
1.下列关于四幅插图的说法正确的是( )
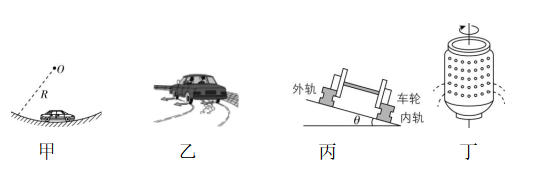
A.甲中汽车通过凹形桥时,汽车需减速,这样可以减小对桥的压力
B.乙中汽车在水平面内转弯时,由地面的滑动摩擦力提供转弯所需的向心力
C.丙中在铁路转弯处的外轨比内轨高,可以减轻转弯时火车内侧轮缘与轨道的挤压
D.丁中洗衣机脱水桶脱水的原因是水滴受到的离心力大于它受到的向心力
答案:A
解析:题图甲中汽车通过凹形桥时,设桥对汽车的支持力为 $ {F}_{\mathrm{N}} $ ,根据牛顿第二定律有 $ {F}_{\mathrm{N}}-mg=m\dfrac{{v}^{2}}{r} $ ,解得 $ {F}_{\mathrm{N}}=mg+m\dfrac{{v}^{2}}{r} $ ,根据牛顿第三定律可知,汽车对桥的压力 $ F{\prime }_{\mathrm{N}}={F}_{\mathrm{N}} $ ,可知汽车需减速,这样可以减小对桥的压力, $ \mathrm{A} $ 正确;题图乙中汽车在水平面内转弯时,由地面的静摩擦力提供转弯所需的向心力, $ \mathrm{B} $ 错误;题图丙中在铁路转弯处的外轨比内轨高,火车所受弹力与水平面有一个夹角,这样一来火车转弯时所需的向心力可以由弹力的水平分力提供,就减轻了转弯时火车外侧轮缘与轨道的挤压, $ \mathrm{C} $ 错误;题图丁中洗衣机脱水桶脱水的原因是水滴受到的合力小于它所需的向心力,做离心运动, $ \mathrm{D} $ 错误.
2.如图所示,蜗杆和蜗轮组成蜗杆传动装置,工作时一般以蜗杆为主动件,当蜗杆旋转时带动蜗轮轮齿沿着蜗杆的螺旋面转动,蜗杆每旋转一圈,蜗轮轮齿会转动一格.若螺距为 $ d=1.6\mathrm{\pi }\mathrm{m}\mathrm{m} $ 的蜗杆以每秒20圈的转速旋转,则半径为 $ r=32\mathrm{m}\mathrm{m} $ 的蜗轮将获得的转速是( )
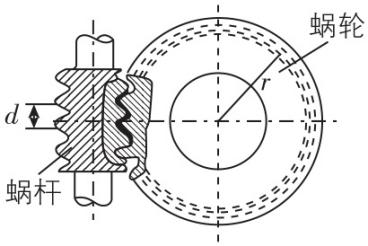
A. $ 30\mathrm{r}/ \min $
B. $ 120\mathrm{r}/ \min $
C. $ 1200\mathrm{r}/ \min $
D. $ 48000\mathrm{r}/ \min $
答案:A
解析:由题意可知,蜗杆每旋转一圈,蜗轮轮齿会转动一格,为齿轮传动模型,线速度相同,有 $ 20d=2\mathrm{\pi }rn $ ,解得 $ n=30\mathrm{r}/ \min $ , $ \mathrm{A} $ 正确.
3.物理学家设计了如图所示的装置.半径为 $ R $ 的圆筒 $ B $ 可绕 $ O $ 轴以角速度 $ \omega $ 匀速转动, $ aOcd $ 在同一直线上,银原子以一定速率从 $ d $ 点沿虚线方向射出,穿过筒上狭缝 $ c $ 打在圆筒内壁 $ b $ 点, $ \mathrm{\angle }aOb=\theta $ , $ ab $ 弧长为 $ s $ ,其间圆筒转过的角度小于 $ {90}^{\circ } $ .下列判断正确的是( )
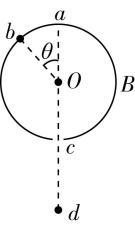
A.圆筒逆时针方向转动
B.银原子在筒内运动时间 $ t=\dfrac{s}{\omega } $
C.银原子速率为 $ \dfrac{\omega R}{\theta } $
D.银原子速率为 $ \dfrac{2\omega {R}^{2}}{s} $
答案:D
解析:由于圆筒转过角度小于 $ {90}^{\circ } $ ,所以圆筒应沿顺时针方向转动,故 $ \mathrm{A} $ 错误;银原子做匀速直线运动,银原子在筒内运动时间 $ t=\dfrac{\theta }{\omega }=\dfrac{s}{R\omega } $ ,故 $ \mathrm{B} $ 错误;由题意可得 $ \dfrac{2R}{v}=\dfrac{s}{R\omega } $ ,解得银原子速率 $ v=\dfrac{2\omega {R}^{2}}{s} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
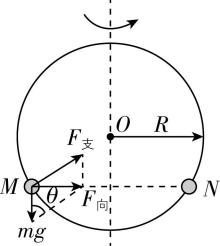
4.某同学设计了一款游戏装置,将两小球 $ M $ 、 $ N $ 套在光滑的圆圈上,小球 $ M $ 的质量大于小球 $ N $ 的质量,然后让圆圈绕竖直中心轴匀速转动,稳定后,下列选项中两小球 $ M $ 、 $ N $ 的位置可能正确的是( )
A.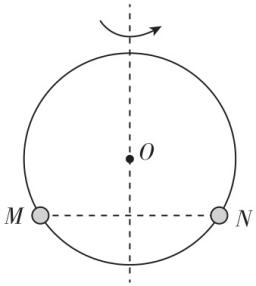
B.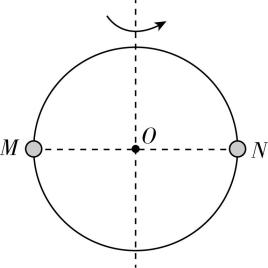
C.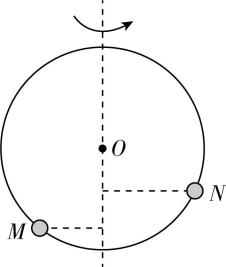
D.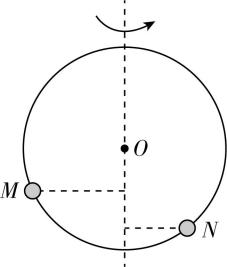
答案:A
解析:稳定后,两小球在水平面内做匀速圆周运动,小球所受重力与圆圈对小球支持力的合力提供向心力,对小球受力分析如图所示,有 $ mg \tan \theta =m{\omega }^{2}R \sin \theta $ ,解得 $ \omega =\sqrt{\dfrac{g}{R \cos \theta }} $ ,两小球转动的角速度相等,所以 $ \theta $ 相同且 $ \theta \ne {90}^{\circ } $ ,两小球在同一水平面内,故选 $ \mathrm{A} $ .
5.如图所示,在距电机轴 $ O $ 为 $ r $ 处有一用轻杆连接的铁块,铁块的质量为 $ m $ ,电机的质量为 $ M $ ,电机启动后,铁块以角速度 $ \omega $ 绕轴 $ O $ 匀速转动,整个过程电机始终静止,已知重力加速度为 $ g $ .下列说法正确的是( )
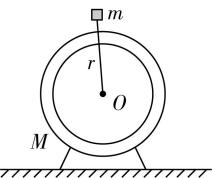
A.铁块运动过程中加速度不变
B.电机对地面的最大压力和最小压力之差为 $ m{\omega }^{2}r $
C.当铁块运动到圆心等高处时,地面对电机的摩擦力为 $ 2m{\omega }^{2}r $
D.若电机始终不脱离地面,铁块的角速度应满足 $ \omega ⩽ \sqrt{\dfrac{Mg+mg}{mr}} $
答案:D
解析:铁块做匀速圆周运动,其加速度始终指向圆心,故加速度大小不变,但方向时刻改变,故 $ \mathrm{A} $ 错误;当铁块运动到最低点时,对铁块,有 $ {N}_{1}-mg=m{\omega }^{2}r $ ,解得 $ {N}_{1}=mg+m{\omega }^{2}r $ ,此时电机对地面的压力最大,为 $ {F}_{\mathrm{N}1}=Mg+mg+m{\omega }^{2}r $ ,同理可知,铁块运动到最高点时,电机对地面的压力最小,为 $ {F}_{\mathrm{N}2}=Mg+mg-m{\omega }^{2}r $ ,故压力差值 $ \mathrm{\Delta }{F}_{\mathrm{N}}={F}_{\mathrm{N}1}-{F}_{\mathrm{N}2}=2mr{\omega }^{2} $ ,故 $ \mathrm{B} $ 错误;当铁块运动到圆心等高处时,向心力大小为 $ {F}_{向}=m{\omega }^{2}r $ ,对电机,水平方向有 $ f={F}_{向}=m{\omega }^{2}r $ ,故 $ \mathrm{C} $ 错误;铁块运动到最高点时,电机对地面的压力最小,当 $ {F}_{\mathrm{N}2}=Mg+mg-m{\omega }^{2}r=0 $ 时,电机恰好不脱离地面,有 $ Mg+mg=m{\omega }^{2}r $ ,解得 $ \omega =\sqrt{\dfrac{Mg+mg}{mr}} $ ,可知若电机始终不脱离地面,铁块的角速度应满足 $ \omega ⩽ \sqrt{\dfrac{Mg+mg}{mr}} $ ,故 $ \mathrm{D} $ 正确.
6.如图所示,支架固定在底座上,它们的总质量为 $ M $ .质量分别为 $ 2m $ 和 $ m $ 的小球 $ A $ 、 $ B $ (可视为质点)固定在一根长度为 $ L $ 的轻杆两端,该轻杆通过光滑转轴 $ O $ 安装在支架的横梁上, $ O $ 、 $ A $ 间的距离为 $ \dfrac{L}{3} $ ,两小球和轻杆一起绕轴 $ O $ 在竖直平面内做圆周运动,运动过程中支架和底座一直保持静止.当转动到图示竖直位置时,小球 $ A $ 的速度为 $ v $ ,重力加速度为 $ g $ .对于该位置,下列说法正确的是( )
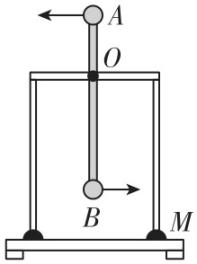
A.小球 $ A $ 、 $ B $ 的向心加速度大小相等
B.小球 $ A $ 的向心力大于小球 $ B $ 的向心力
C.若 $ v=\sqrt{\dfrac{gL}{3}} $ ,则底座对水平地面的压力大小为 $ Mg+2mg $
D.若 $ v=\sqrt{\dfrac{gL}{3}} $ ,则底座对水平地面的压力大小为 $ Mg+3mg $
答案:D
解析:两小球和轻杆一起绕轴 $ O $ 在竖直平面内做圆周运动,所以两小球的角速度相同,根据 $ a={\omega }^{2}r $ ,可知小球 $ A $ 、 $ B $ 的加速度大小之比为 $ {a}_{A}:{a}_{B}=1:2 $ ,故 $ \mathrm{A} $ 错误;根据 $ F=ma $ ,可知 $ A $ 、 $ B $ 的向心力之比为 $ {F}_{A}:{F}_{B}=1:1 $ ,故 $ \mathrm{B} $ 错误;若 $ v=\sqrt{\dfrac{gL}{3}} $ ,对 $ A $ 有 $ 2mg-{F}_{\mathrm{N}A}=\dfrac{2m{v}^{2}}{\dfrac{L}{3}} $ ,解得轻杆对 $ A $ 的支持力为 $ {F}_{\mathrm{N}A}=0 $ ,根据 $ v=\omega r $ ,可知 $ {v}_{B}=2\sqrt{\dfrac{gL}{3}} $ ,对 $ B $ 有 $ {F}_{\mathrm{N}B}-mg=\dfrac{m{v}_{B}^{2}}{\dfrac{2L}{3}} $ ,解得轻杆对 $ B $ 的拉力大小为 $ {F}_{\mathrm{N}B}=3mg $ ,由牛顿第三定律可知, $ B $ 对轻杆的拉力大小为 $ F{\prime }_{\mathrm{N}B}={F}_{\mathrm{N}B}=3mg $ ,方向向下,以支架、底座和轻杆整体为研究对象,水平地面对底座的支持力为 $ N=Mg+F{\prime }_{\mathrm{N}B}=Mg+3mg $ ,根据牛顿第三定律可知,底座对水平地面的压力大小为 $ Mg+3mg $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
7.压缩机通过活塞在汽缸内做往复运动来压缩和输送气体,活塞的中心 $ A $ 与圆盘在同一平面内, $ O $ 为圆盘圆心, $ B $ 为圆盘上一点, $ A $ 、 $ B $ 处通过铰链连接在轻杆两端,圆盘以角速度 $ \omega $ 匀速转动,如图所示, $ OC\perp OA $ , $ OB\perp AB $ ,则( )
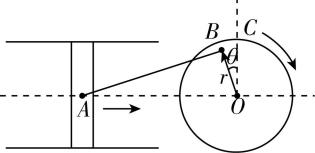
A.杆越长,活塞运动的范围越大
B.圆盘从图示位置转过 $ \theta $ 角的过程中活塞移动的距离比再转过 $ \theta $ 角大
C.图示位置时的活塞速度小于圆盘转过 $ \theta $ 角时的活塞速度
D.图示位置时的活塞速度等于圆盘转过 $ \theta $ 角时的活塞速度
答案:B
解析:当 $ B $ 点在圆心左侧水平位置时,活塞运动到最左端,距离 $ O $ 点为 $ {s}_{1}=L+r $ ,当 $ B $ 点在圆心右侧水平位置时,活塞运动到最右端,距离 $ O $ 点为 $ {s}_{2}=L-r $ ,活塞运动范围为 $ {s}_{1}-{s}_{2}=2r $ ,与 $ L $ 无关,与 $ r $ 成正比,故 $ \mathrm{A} $ 错误;设杆长为 $ nr $ , $ n > 2 $ , $ \tan \theta =\dfrac{1}{n} $ ,由几何知识得 $ \sqrt{{r}^{2}+{\left(nr\right) ^ {2}}}=\sqrt{{n}^{2}+1}\cdot r $ , $ \sqrt{{n}^{2}{r}^{2}-{r}^{2}}=\sqrt{{n}^{2}-1}\cdot r $ ,圆盘从图示位置转过 $ \theta $ 角,活塞移动的距离 $ \mathrm{\Delta }x=r(\sqrt{{n}^{2}+1}-\sqrt{{n}^{2}-1}) $ ,圆盘再转过 $ \theta $ 角,由几何知识得 $ {x}^{2}+{r}^{2}-2rx \cos ({90}^{\circ }+\theta )={n}^{2}{r}^{2} $ ,活塞移动的距离 $ \mathrm{\Delta }x^\prime =\sqrt{{n}^{2}-1}\cdot r-x=(\sqrt{{n}^{2}-1}-\dfrac{{n}^{2}-1}{\sqrt{{n}^{2}+1}})r $ ,可知 $ \mathrm{\Delta }x > \mathrm{\Delta }x^\prime $ ,故 $ \mathrm{B} $ 正确;图示位置时,即 $ OB $ 垂直于 $ AB $ ,此时 $ B $ 点的速度方向一定沿杆,则 $ {v}_{A} \cos \theta ={v}_{B}=\omega r $ ,圆盘转过 $ \theta $ 角时,即 $ OB $ 垂直于 $ AO $ ,活塞速度方向与圆盘上 $ B $ 点速度方向相同,则 $ v{\prime }_{A}={v}_{B}=\omega r $ ,可知 $ {v}_{A} > v{\prime }_{A} $ ,故 $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误.
8.如图所示,某同学手握一段硬质细塑料管,一根不可伸长的细线穿过塑料管,细线一端连接小球 $ A $ ,另一端连接物块 $ B $ .现该同学通过摇动手中塑料管,使小球 $ A $ 在水平面内做匀速圆周运动,物块 $ B $ 处于静止状态.初始时刻小球 $ A $ 的速度大小为 $ {v}_{1} $ ,细线与竖直方向的夹角为 $ {\theta }_{1} $ ,塑料管口与小球 $ A $ 之间的细线长为 $ {L}_{1} $ .改变物块 $ B $ 的高度后,再次让小球 $ A $ 在水平面内做匀速圆周运动,物块 $ B $ 仍处于静止状态,此时小球 $ A $ 的速度大小为 $ {v}_{2} $ ,且 $ {v}_{1} < {v}_{2} $ ,细线与竖直方向的夹角为 $ {\theta }_{2} $ ,塑料管口与小球 $ A $ 之间的细线长为 $ {L}_{2} $ ,不计空气阻力,忽略细线与塑料管之间的摩擦,小球 $ A $ 在做匀速圆周运动时,可认为塑料管静止.则下列说法正确的是( )
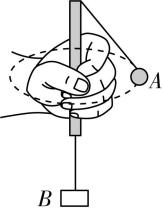 (多选)
(多选)
A. $ {\theta }_{1}={\theta }_{2} $
B. $ {\theta }_{1} > {\theta }_{2} $
C. $ {L}_{1} > {L}_{2} $
D. $ {L}_{1} < {L}_{2} $
答案:AD
解析:设 $ A $ 、 $ B $ 的质量分别为 $ {m}_{A} $ 和 $ {m}_{B} $ ,对小球 $ A $ 受力分析,则有 $ T \cos \theta ={m}_{A}g $ ,对 $ B $ ,有 $ T={m}_{B}g $ ,解得 $ \cos \theta =\dfrac{{m}_{A}}{{m}_{B}} $ ,可知 $ \theta $ 不变,即 $ {\theta }_{1}={\theta }_{2} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误; $ A $ 做匀速圆周运动,有 $ {m}_{B}g \sin \theta ={m}_{A}\frac{{v}^{2}}{L \sin \theta } $ ,解得 $ L=\dfrac{{m}_{A}}{{m}_{B}g{ \sin }^{2}\theta }{v}^{2}=\dfrac{{v}^{2} \cos \theta }{g{ \sin }^{2}\theta } $ ,因为 $ \theta $ 不变, $ {v}_{2} > {v}_{1} $ ,所以 $ {L}_{2} > {L}_{1} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
9.如图甲所示,质量均为 $ m $ 的两个物块 $ A $ 、 $ B $ 用不可伸长的轻绳相连,放在水平转盘上,初始状态绳子伸直但无拉力.已知两物块与转盘之间的动摩擦因数均为 $ \mu $ ,最大静摩擦力等于滑动摩擦力,重力加速度大小为 $ g $ .现让转盘从静止缓慢增加转速.两物块所受摩擦力随角速度平方的变化图像如图乙所示,取摩擦力由 $ B $ 指向 $ A $ 为正方向,则( )
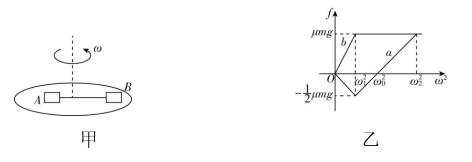 (多选)
(多选)
A.乙图中 $ b $ 对应 $ B $ 物块所受摩擦力随角速度平方的变化图像
B. $ A $ 、 $ B $ 两物块到转盘圆心的距离之比为 $ 1:2 $
C. $ {\omega }_{1}^{2}:{\omega }_{0}^{2}:{\omega }_{2}^{2}=1:2:4 $
D.当 $ \omega ={\omega }_{2} $ 时,绳上的张力大小为 $ 2\mu mg $
答案:ABC
解析:转盘从静止缓慢增加转速,绳上有拉力前, $ A $ 、 $ B $ 两物块靠静摩擦力提供向心力, $ A $ 所受摩擦力由 $ A $ 指向 $ B $ , $ B $ 所受摩擦力由 $ B $ 指向 $ A $ ,由题图乙可知 $ b $ 为 $ B $ 物块所受摩擦力随角速度平方的变化图像,故 $ \mathrm{A} $ 正确;当 $ B $ 达到最大静摩擦力时有 $ \mu mg=m{\omega }_{1}^{2}{r}_{B} $ ,此时对 $ A $ 物块,有 $ \dfrac{1}{2}\mu mg=m{\omega }_{1}^{2}{r}_{A} $ ,联立可得 $ {r}_{B}=2{r}_{A} $ , $ {\omega }_{1}^{2}=\dfrac{\mu g}{{r}_{B}} $ ,故 $ \mathrm{B} $ 正确;设绳上拉力为 $ T $ , $ A $ 做圆周运动的半径为 $ r $ , $ B $ 做圆周运动的半径为 $ 2r $ ,当 $ \omega ={\omega }_{0} $ 时,对 $ B $ 有 $ T+\mu mg=m{\omega }_{0}^{2}\cdot 2r $ ,对 $ A $ 有 $ T=m{\omega }_{0}^{2}r $ ,解得 $ {\omega }_{0}^{2}=\dfrac{\mu g}{r} $ ,当 $ \omega ={\omega }_{2} $ 时,对 $ A $ 有 $ T^\prime -\mu mg=m{\omega }_{2}^{2}r $ ,对 $ B $ 有 $ T^\prime +\mu mg=m{\omega }_{2}^{2}\cdot 2r $ ,联立可得 $ {\omega }_{2}^{2}=\dfrac{2\mu g}{r} $ , $ T^\prime =3\mu mg $ ,可得 $ {\omega }_{1}^{2}:{\omega }_{0}^{2}:{\omega }_{2}^{2}=\dfrac{\mu g}{2r}:\dfrac{\mu g}{r}:\dfrac{2\mu g}{r}=1:2:4 $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
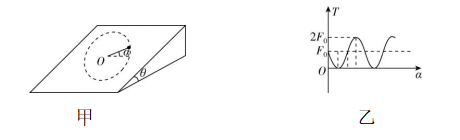
10.如图甲所示,倾角为 $ \theta $ 的光滑斜面固定在水平地面上,细线一端与可看成质点的质量为 $ m $ 的小球相连,另一端穿入小孔 $ O $ 与力传感器(位于斜面体内部)连接,力传感器可实时记录细线拉力大小及扫过的角度.初始时,细线水平,小球位于小孔 $ O $ 的右侧,现敲击小球,使小球获得一平行于斜面向上的初速度 $ {v}_{0} $ ,此后力传感器记录细线拉力 $ T $ 的大小随细线扫过角度 $ \alpha $ 的变化图像如图乙所示,图中 $ {F}_{0} $ 已知,小球到 $ O $ 点的距离为 $ l $ ,重力加速度为 $ g $ ,则下列说法正确的是( )
 (多选)
(多选)
A.小球位于初始位置时的加速度大小为 $ \dfrac{{v}_{0}^{2}}{l} $
B.小球通过最高点时速度大小为 $ \sqrt{gl} $
C.小球通过最高点时速度大小为 $ \sqrt{\dfrac{mg \sin \theta }{{F}_{0}}}{v}_{0} $
D.小球通过最低点时速度大小为 $ \sqrt{\dfrac{2{F}_{0}-mg \sin \theta }{{F}_{0}}}{v}_{0} $
答案:CD
解析:小球位于初始位置时的向心加速度大小为 $ {a}_{1}=\dfrac{{v}_{0}^{2}}{l} $ ,沿斜面向下的加速度大小 $ {a}_{2}=g \sin \theta $ ,则小球位于初始位置时的加速度大于 $ \dfrac{{v}_{0}^{2}}{l} $ , $ \mathrm{A} $ 错误;由题图乙可知,小球通过最高点时细线的拉力为零,有 $ mg \sin \theta =m\dfrac{{v}_{1}^{2}}{l} $ ,解得小球通过最高点时速度大小为 $ {v}_{1}=\sqrt{gl \sin \theta } $ , $ \mathrm{B} $ 错误;小球在初始位置时,有 $ {F}_{0}=m\dfrac{{v}_{0}^{2}}{l} $ ,则小球通过最高点时速度大小为 $ {v}_{1}=\sqrt{gl \sin \theta }=\sqrt{\dfrac{mg \sin \theta }{{F}_{0}}}{v}_{0} $ , $ \mathrm{C} $ 正确;小球通过最低点时,有 $ 2{F}_{0}-mg \sin \theta =m\dfrac{{v}_{2}^{2}}{l} $ ,解得小球通过最低点时速度大小为 $ {v}_{2}=\sqrt{\dfrac{2{F}_{0}-mg \sin \theta }{{F}_{0}}}{v}_{0} $ , $ \mathrm{D} $ 正确.
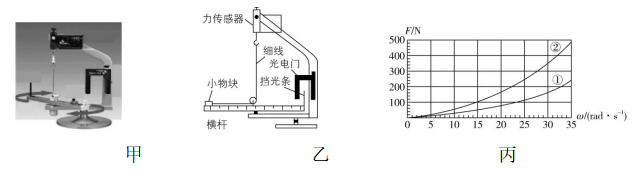
11.(6分)向心力实验装置和示意图如图甲、乙所示,可以用来探究影响向心力大小的因素,实验中可以用力传感器测出小物块在水平光滑的横杆上做圆周运动所需要的向心力大小,用光电门传感器辅助测量小物块转动的角速度.
(1) 本实验所采用的实验探究方法与以下问题研究方法相同的是 .
A.求匀变速直线运动的位移
B.“瞬时速度”概念的建立
C.通过平面镜观察桌面的微小形变
D.探究加速度与物体受力、物体质量的关系
(2) 实验时,测得挡光条的宽度为 $ 3\mathrm{m}\mathrm{m} $ ,某次旋转过程中挡光条的旋转半径为 $ 0.20\mathrm{m} $ ,挡光条经过光电门时的挡光时间 $ \mathrm{\Delta }t=1.2×{10}^{-3}\mathrm{s} $ ,则小物块做圆周运动的角速度 $ \omega = $ $ \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ .
(3) 图丙中①②两条曲线为相同半径、不同质量的小物块的向心力与角速度的关系图线,由图丙可知,曲线①对应的小物块质量 (填“大于”或“小于”)曲线②对应的小物块质量.
解析:(1) 本实验所采用的探究方法是控制变量法,求匀变速直线运动的位移,采用的是微元累积法,“瞬时速度”概念的建立,采用的是极限思想方法,通过平面镜观察桌面的微小形变,采用了放大法的物理思想,探究加速度与物体受力、物体质量的关系采用了控制变量法,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 、 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
(2) 根据极短时间内的平均速度等于瞬时速度,可知挡光条处的线速度 $ v=\dfrac{d}{\mathrm{\Delta }t} $ ,由 $ v=\omega r $ ,可得小物块的角速度为 $ \omega =\dfrac{v}{r}=\dfrac{d}{r\mathrm{\Delta }t} $ ,代入数据可得 $ \omega =12.5\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ .
(3) 若保持角速度和半径都不变,由牛顿第二定律有 $ F=m{\omega }^{2}r $ ,可知半径相同, $ \omega $ 一定时,质量大的小物块需要的向心力大,所以曲线①对应的小物块质量小于曲线②对应的小物块质量.
12.(14分)如图甲为自动分拣装置图,由长为 $ 8.0\mathrm{m} $ 的直线水平传送带 $ PM $ 和半径为 $ 4.0\mathrm{m} $ 的水平圆弧传送带 $ MN $ 平滑连接而成,其俯视示意图如图乙所示.将一个质量为 $ 2\mathrm{k}\mathrm{g} $ 的小工件轻放在 $ P $ 处后被传送至 $ N $ 处.已知小工件与两部分传送带间的动摩擦因数均为 $ \mu =0.2 $ ,传送带中线 $ PMN $ 上各处的速率均为 $ 1.0\mathrm{m}/\mathrm{s} $ ,设最大静摩擦力等于滑动摩擦力,重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ .求:

(1) 小工件到达 $ M $ 点的速度大小;
(2) 小工件从 $ M $ 运动到 $ N $ 的过程中向心加速度大小和摩擦力大小.
答案:(1) $ 1\mathrm{m}/\mathrm{s} $
(2) $ 0.25\mathrm{m}/{\mathrm{s}}^{2} $ $ 0.5\mathrm{N} $
解析:(1) 小工件先在 $ PM $ 上做匀加速直线运动,有 $ \mu mg=m{a}_{1} $ ,解得 $ {a}_{1}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,
小工件与传送带共速所用时间为 $ t=\dfrac{v}{{a}_{1}}=0.5\mathrm{s} $ ,
小工件加速运动的位移大小为 $ x=\dfrac{1}{2}{a}_{1}{t}^{2}=0.25\mathrm{m} < 8\mathrm{m} $ ,
故小工件到达 $ M $ 点的速度大小为 $ 1\mathrm{m}/\mathrm{s} $ .
(2) 小工件的向心加速度大小为 $ {a}_{2}=\dfrac{{v}^{2}}{R}=0.25\mathrm{m}/{\mathrm{s}}^{2} $ ,
小工件所受的摩擦力大小为 $ f=m{a}_{2}=0.5\mathrm{N} $ .
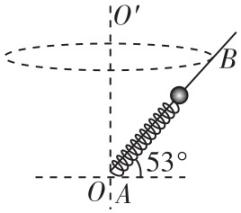
13.(16分)如图所示,一根原长为 $ L=0.1\mathrm{m} $ 的轻弹簧套在一长为 $ 1.8L $ 的光滑直杆 $ AB $ 上,其下端固定在杆的 $ A $ 端,质量为 $ m=1\mathrm{k}\mathrm{g} $ 的小球也套在杆上且与弹簧的上端相连.小球和杆一起绕过杆 $ A $ 端的竖直轴 $ OO\prime $ 匀速转动,且杆与水平面间始终保持 $ \theta ={53}^{\circ } $ 角.已知杆处于静止状态时弹簧长度为 $ 0.6L $ , $ \sin {53}^{\circ }=0.8 $ , $ \cos {53}^{\circ }=0.6 $ ,重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,求:
(1) 弹簧的劲度系数 $ k $ ;
(2) 弹簧为原长时,小球的角速度 $ {\omega }_{0} $ ;(结果可含根号)
(3) 当杆的角速度满足什么条件时小球会从 $ B $ 端飞出.(结果可含根号)
答案:(1) $ 200\mathrm{N}/\mathrm{m} $
(2) $ \dfrac{20\sqrt{5}}{3}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
(3) $ \omega > \dfrac{100\sqrt{3}}{9}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $
解析:(1) 杆处于静止状态时,对小球受力分析,由平衡条件得 $ mg \sin \theta ={F}_{弹} $ ,根据胡克定律得 $ {F}_{弹}=k(L-0.6L) $ ,解得 $ k=200\mathrm{N}/\mathrm{m} $ .
(2) 弹簧为原长时,小球只受重力和杆的支持力,有 $ mg \tan \theta ={\rm mL} \cos \theta \cdot {\omega }_{0}^{2} $ ,解得 $ {\omega }_{0}=\dfrac{20\sqrt{5}}{3}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ .
(3) 当弹簧伸长量为 $ 0.8L $ 时,小球恰好不会从 $ B $ 端飞出,设此时弹簧的弹力为 $ F $ ,对小球受力分析可得,竖直方向上有 $ {F}_{\mathrm{N}} \cos \theta =mg+F \sin \theta $ ,水平方向上有 $ {F}_{\mathrm{N}} \sin \theta +F \cos \theta =m(L+0.8L) \cos \theta \cdot {\omega }_{1}^{2} $ ,根据胡克定律得 $ F=k\cdot 0.8L $ ,解得 $ {\omega }_{1}=\dfrac{100\sqrt{3}}{9}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ ,所以当杆的角速度 $ \omega > \dfrac{100\sqrt{3}}{9}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} $ 时,小球会从 $ B $ 端飞出.
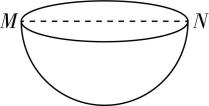
14.(18分)如图所示,倾角为 $ \theta ={37}^{\circ } $ 的光滑斜面体固定在水平地面上,在斜面上固定一个光滑的半圆形挡板 $ AEB $ ,半径为 $ r=1\mathrm{m} $ ,其最低点 $ A $ 、最高点 $ B $ 的切线水平, $ AB $ 是半圆形挡板的直径, $ OE $ 垂直于边 $ AB $ 和 $ CD $ ,斜面体右侧地面上有半径为 $ R=1.15\mathrm{m} $ 的半球形容器,直径 $ MN $ 和矩形 $ BCQP $ 在同一竖直面内, $ M $ 点到 $ BP $ 的水平距离为 $ L=0.3\mathrm{m} $ .重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,忽略空气阻力, $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ ,现让质量为 $ m $ 的小球(可视为质点)从 $ A $ 点以一定的水平速度滑进 $ AEB $ .
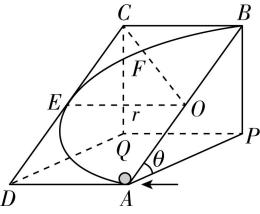
(1) 若小球恰好从 $ B $ 点飞出,求通过 $ B $ 点的速度大小;
(2) 若小球从 $ B $ 点以速度 $ {v}_{0} $ 飞出,要落入右边的容器中,则 $ {v}_{0} $ 需满足什么条件?
(3) 若小球从 $ A $ 点进入后运动到图中 $ F $ 点(半圆形挡板与 $ OC $ 的交点)时离开挡板,求经过 $ F $ 点时的速度大小 $ {v}_{F} $ .(结果可带根号)
答案:(1) $ \sqrt{6}\mathrm{m}/\mathrm{s} $
(2) $ 3\mathrm{m}/\mathrm{s} < {v}_{0} < 26\mathrm{m}/\mathrm{s} $
(3) $ \sqrt{3\sqrt{2}}\mathrm{m}/\mathrm{s} $
解析:(1) 当小球恰好从 $ B $ 点飞出时,此时对挡板的压力 $ N=0 $ ,如图甲所示,
由牛顿第二定律可得 $ {G}_{1}=mg \sin \theta =\dfrac{m{v}_{B}^{2}}{r} $ ,
代入数据解得 $ {v}_{B}=\sqrt{6}\mathrm{m}/\mathrm{s} $ .
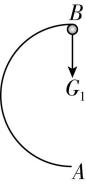
甲
(2) 小球从 $ B $ 点飞出后,做平抛运动,有
$ 2r \sin \theta -R=\dfrac{1}{2}g{t}^{2} $ , $ x={v}_{0}t $ ,
根据题意可知 $ L < x < L+2R $ ,
联立解得 $ 3\mathrm{m}/\mathrm{s} < {v}_{0} < 26\mathrm{m}/\mathrm{s} $ .
(3) 当小球从 $ F $ 点离开挡板时,如图乙所示,
此时对挡板的压力 $ N^\prime =0 $ ,
由牛顿第二定律可得
$ {G}_{1} \sin \beta =mg \sin \theta \sin \beta =\dfrac{m{v}_{F}^{2}}{r} $ ,
由几何关系可知 $ \beta ={45}^{\circ } $ ,代入数据解得 $ {v}_{F}=\sqrt{3\sqrt{2}}\mathrm{m}/\mathrm{s} $ .
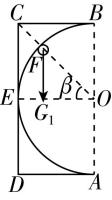
乙











 (多选)
(多选)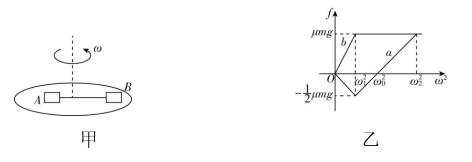 (多选)
(多选) (多选)
(多选)



