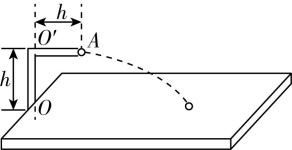
1.如图所示,乒乓球的发射器安装在水平桌面上,发射器出口距桌面的高度为 $ h $ ,发射器 $ O^\prime A $ 的长度也为 $ h $ ,打开开关后,可将乒乓球从 $ A $ 点以初速度 $ {v}_{0} $ 水平发射出去,其中 $ \sqrt{\dfrac{gh}{2}}⩽ {v}_{0}⩽ \sqrt{\dfrac{9gh}{2}} $ ( $ g $ 为重力加速度).设发射器发射出的所有乒乓球都能落到桌面上,乒乓球可视为质点,空气阻力不计.若使该发射器绕转轴 $ OO\prime $ 在 $ {60}^{\circ } $ 角的范围内来回缓慢水平转动,持续发射足够长时间后,乒乓球第一次与桌面相碰的区域的最大面积为( )
A. $ 2\mathrm{\pi }{h}^{2} $
B. $ 3\mathrm{\pi }{h}^{2} $
C. $ 4\mathrm{\pi }{h}^{2} $
D. $ 8\mathrm{\pi }{h}^{2} $
乒乓球做平抛运动,在空中运动的时间为 $ t=\sqrt{\dfrac{2h}{g}} $ ,水平位移为 $ x={v}_{0}t $ ,结合 $ \sqrt{\dfrac{gh}{2}}⩽ {v}_{0}⩽ \sqrt{\dfrac{9gh}{2}} $ ,解得 $ h⩽ x⩽ 3h $ ,乒乓球的落点区域为六分之一圆环,其内径为 $ 2h $ 、外径为 $ 4h $ ,可得乒乓球第一次与桌面相碰的区域最大面积为 $ {S}_{\mathrm{m}}=\dfrac{1}{6} [\mathrm{\pi } (4h)^{2}-\mathrm{\pi } (2h)^{2} ]=2\mathrm{\pi }{h}^{2} $ , $ \mathrm{A} $ 正确.
 (多选)
(多选)