课时2 平抛运动与斜面、曲面的综合应用
一、刷基础
1.如图所示,从倾角为 $ \theta $ 的足够长的斜面顶端 $ P $ 以初速度 $ {v}_{0} $ 水平抛出一个小球,落在斜面上 $ Q $ 点,小球落在斜面上的速度与斜面的夹角为 $ \alpha $ ,若把水平抛出时的初速度变为 $ 2{v}_{0} $ ,小球仍落在斜面上,则下列说法正确的是( )
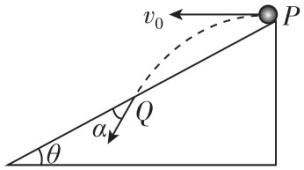
A.小球落在斜面上的速度与斜面的夹角 $ \alpha $ 将变大
B. $ PQ $ 间距变为原来的2倍
C.小球做平抛运动的时间变为原来的2倍
D.小球落在斜面上的速度大于原来的2倍
答案:C
解析:根据平抛运动规律知 $ \tan \theta =\dfrac{y}{x}=\dfrac{\dfrac{1}{2}g{t}^{2}}{{v}_{0}t}=\dfrac{gt}{2{v}_{0}} $ , $ \tan (\alpha +\theta )=\dfrac{{v}_{y}}{{v}_{x}}=\dfrac{gt}{{v}_{0}} $ ,所以 $ \tan (\alpha +\theta )=2 \tan \theta $ ,倾角 $ \theta $ 为定值,所以小球落在斜面上时速度与斜面的夹角 $ \alpha $ 为定值,与速度大小无关, $ \mathrm{A} $ 错误;由上述分析可得 $ t=\dfrac{2{v}_{0} \tan \theta }{g} $ ,小球初速度变为 $ 2{v}_{0} $ 时,做平抛运动的时间变为原来的2倍, $ \mathrm{C} $ 正确; $ PQ $ 间距 $ s=\dfrac{{v}_{0}t}{ \cos \theta }=\dfrac{2{v}_{0}^{2} \tan \theta }{g \cos \theta } $ ,小球初速度变为 $ 2{v}_{0} $ 时, $ PQ $ 间距变为原来的4倍, $ \mathrm{B} $ 错误;小球落在斜面上时的速度大小 $ v=\sqrt{{v}_{0}^{2}+{\left(gt\right) ^ {2}}}=\sqrt{{v}_{0}^{2}+{\left(2{v}_{0} \tan \theta \right) ^ {2}}}={v}_{0}\sqrt{1+4{ \tan }^{2}\theta } $ ,初速度变为 $ 2{v}_{0} $ 时,落在斜面上时的速度等于原来的2倍, $ \mathrm{D} $ 错误.
2.如图,两小球 $ P $ 、 $ Q $ 从同一高度分别以 $ {v}_{1} $ 和 $ {v}_{2} $ 的初速度水平抛出;都落在了斜面上的 $ A $ 点,其中小球 $ P $ 垂直打到斜面上,若斜面倾角 $ \theta ={37}^{\circ } $ ,则 $ {v}_{1} $ 、 $ {v}_{2} $ 大小之比为 $ ( \sin {37}^{\circ }=0.6, \cos {37}^{\circ }=0.8) $ ( )
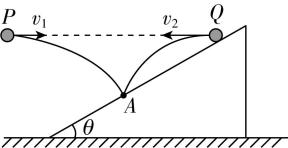
A. $ 9:8 $
B. $ 8:9 $
C. $ 32:9 $
D. $ 9:32 $
答案:A
解析:因为两小球从同一高度抛出落到同一点,下落高度相同,根据 $ ℎ=\dfrac{1}{2}g{t}^{2} $ 可知,两球运动时间 $ t $ 相等;小球 $ P $ 垂直打在斜面上,根据几何关系有 $ \tan \theta =\dfrac{{v}_{1}}{gt} $ ,小球 $ Q $ 落在斜面上时,根据几何关系有 $ \tan \theta =\dfrac{\dfrac{1}{2}g{t}^{2}}{{v}_{2}t}=\dfrac{gt}{2{v}_{2}} $ ,联立可得 $ \dfrac{{v}_{1}}{{v}_{2}}=\dfrac{2{ \tan }^{2}\theta }{1}=\dfrac{9}{8} $ ,故选 $ \mathrm{A} $ .
3.如图所示,光滑的水平桌面上,小球以 $ {v}_{0}=10\mathrm{m}/\mathrm{s} $ 的初速度从边缘 $ A $ 点离开桌面做平抛运动,运动过程中轨迹恰好与放置在水平地面上的半圆柱体相切于 $ P $ 点,桌面与地面的高度差为 $ ℎ $ , $ BC $ 是半圆柱体横截面的直径, $ B $ 在 $ A $ 的正下方, $ O $ 是半圆柱体横截面的圆心, $ OP $ 与水平面的夹角 $ \theta ={60}^{\circ } $ , $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,则( )
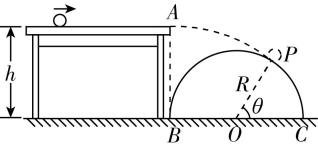 (多选)
(多选)
A.小球在 $ P $ 点时的速度方向与水平方向的夹角为 $ {60}^{\circ } $
B.小球从 $ A $ 到 $ P $ 的运动时间为 $ \dfrac{\sqrt{3}}{3}\mathrm{s} $
C.半圆柱体的半径为 $ \dfrac{20\sqrt{3}}{9}\mathrm{m} $
D.桌面与地面的高度差为 $ ℎ=2.5\mathrm{m} $
答案:BC
解析:由几何关系可知,小球在 $ P $ 点时的速度方向与水平方向的夹角为 $ {30}^{\circ } $ ,故 $ \mathrm{A} $ 错误;设小球从 $ A $ 点到 $ P $ 点的运动时间为 $ t $ ,将小球在 $ P $ 点时的速度分别沿水平和竖直方向分解,可得 $ \dfrac{{v}_{0}}{gt}= \tan \theta $ ,解得 $ t=\dfrac{\sqrt{3}}{3}\mathrm{s} $ ,故 $ \mathrm{B} $ 正确;小球做平抛运动的水平位移、竖直位移分别为 $ x={v}_{0}t $ 、 $ y=\dfrac{1}{2}g{t}^{2} $ ,由几何关系可得 $ R \cos \theta +R=x $ , $ R \sin \theta +y=ℎ $ ,联立解得 $ R=\dfrac{20\sqrt{3}}{9}\mathrm{m} $ , $ ℎ=5\mathrm{m} $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
4.如图所示为半球形碗的竖直截面图, $ O $ 为圆心, $ C $ 为半球形碗的最低点, $ AOB $ 为水平直径,碗的半径为 $ r $ .两个小球甲和乙先后分别从 $ A $ 点、 $ B $ 点以不同的初速度 $ {v}_{1} $ 、 $ {v}_{2} $ 沿水平方向相向抛出,小球甲恰好撞到碗上的 $ C $ 点, $ {v}_{2}=\dfrac{{v}_{1}}{2} $ .两小球可视为质点,撞到碗后不反弹,忽略空气阻力,重力加速度为 $ g $ .则( )
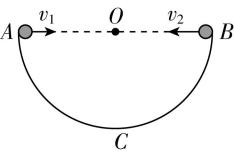 (多选)
(多选)
A.两小球能在空中相遇
B.小球乙不可能垂直撞击到碗上
C.小球甲刚要撞到碗时的竖直分速度比乙刚要撞到碗时的竖直分速度大
D.小球乙的初速度 $ {v}_{2}=\dfrac{\sqrt{2gr}}{2} $
答案:BC
解析:两个小球甲和乙是先后做的平抛运动, $ {ℎ}_{1}=\dfrac{1}{2}g{t}_{1}^{2} $ , $ {ℎ}_{2}=\dfrac{1}{2}g{t}_{2}^{2} $ , $ {t}_{1} $ 与 $ {t}_{2} $ 不相同,所以两小球不可能在空中相遇, $ \mathrm{A} $ 错误;由平抛运动推论可知,速度反向延长线一定过水平位移中点,若小球乙垂直撞到碗上,则速度反向延长线应过 $ O $ 点,分析可知小球乙速度反向延长线不会过 $ O $ 点,则小球乙不可能垂直撞击到碗上, $ \mathrm{B} $ 正确;由平抛运动规律可知,下落高度越大,竖直分速度越大,所以竖直分速度最大时平抛落点为 $ C $ 点,由平抛运动规律可得 $ r=\dfrac{1}{2}g{t}^{2} $ , $ r={v}_{1}t $ ,解得 $ {v}_{1}=\dfrac{\sqrt{2gr}}{2} $ ,因为 $ {v}_{2}=\dfrac{{v}_{1}}{2} $ ,所以 $ {v}_{2}=\dfrac{\sqrt{2gr}}{4} $ , $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
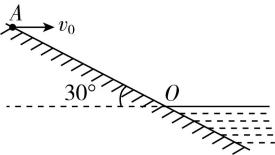
5.如图为湖边一倾角为 $ {30}^{\circ } $ 的大坝的横截面示意图,水面与大坝的交点为 $ O $ .一人站在 $ A $ 点处以速度 $ {v}_{0} $ 沿水平方向扔小石块,已知 $ AO=40\mathrm{m} $ ,重力加速度 $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,忽略人的身高,不计空气阻力.下列说法正确的是( )
 (多选)
(多选)
A.若 $ {v}_{0}⩾ 10\sqrt{3}\mathrm{m}/\mathrm{s} $ ,则石块平抛运动的时间一定为 $ 2\mathrm{s} $
B.若 $ {v}_{0}=10\mathrm{m}/\mathrm{s} $ ,石块平抛运动的时间为 $ \sqrt{3}\mathrm{s} $
C.若石块落到斜面上,则石块落到斜面上时速度方向与斜面的夹角与 $ {v}_{0} $ 无关
D.若石块能落入水中,则 $ {v}_{0} $ 越大,落水时速度方向与水平面的夹角越大
答案:AC
解析:若石块恰落到 $ O $ 点,则 $ AO \cos {30}^{\circ }={v}_{0}t $ , $ AO \sin {30}^{\circ }=\dfrac{1}{2}g{t}^{2} $ ,可得 $ t=2\mathrm{s} $ , $ {v}_{0}=10\sqrt{3}\mathrm{m}/\mathrm{s} $ ,若 $ {v}_{0}⩾ 10\sqrt{3}\mathrm{m}/\mathrm{s} $ ,则石块一定会落在水面上,即平抛运动的时间一定为 $ 2\mathrm{s} $ , $ \mathrm{A} $ 正确;若 $ {v}_{0}=10\mathrm{m}/\mathrm{s} $ ,石块将落在斜面上,根据 $ \tan {30}^{\circ }=\dfrac{\dfrac{1}{2}g{t}^{2}}{{v}_{0}t}=\dfrac{gt}{2{v}_{0}} $ ,可得石块平抛运动的时间为 $ t=\dfrac{2\sqrt{3}}{3}\mathrm{s} $ , $ \mathrm{B} $ 错误;若石块落到斜面上,设石块落到斜面上时速度方向与斜面的夹角为 $ \alpha $ ,则有 $ \tan (\alpha +{30}^{\circ })=\dfrac{gt}{{v}_{0}}=2\dfrac{\dfrac{1}{2}g{t}^{2}}{{v}_{0}t}=2 \tan {30}^{\circ } $ ,即 $ \alpha $ 为定值,与 $ {v}_{0} $ 无关, $ \mathrm{C} $ 正确;若石块能落入水中,设落水时速度方向与水平面的夹角为 $ \beta $ ,则有 $ \tan \beta =\dfrac{{v}_{y}}{{v}_{0}}=\dfrac{\sqrt{2gℎ}}{{v}_{0}} $ ,则 $ {v}_{0} $ 越大,落水时速度方向与水平面的夹角越小, $ \mathrm{D} $ 错误.
二、刷提升
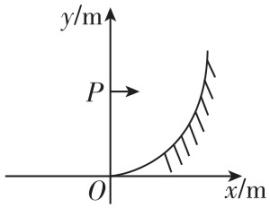
1.如图所示,在竖直平面内有一曲面,曲面方程为 $ y={x}^{2} $ ,在 $ y $ 轴上有一点 $ P $ ,坐标为 $ (0,6\mathrm{m}) $ .从 $ P $ 点将一小球水平抛出,初速度为 $ 1\mathrm{m}/\mathrm{s} $ ,则小球第一次打在曲面上的位置为(不计空气阻力, $ g $ 取 $ 10\mathrm{m}/{\mathrm{s}}^{2} $ )( )
A. $ (3\mathrm{m},3\mathrm{m}) $
B. $ (2\mathrm{m},4\mathrm{m}) $
C. $ (1\mathrm{m},1\mathrm{m}) $
D. $ (1\mathrm{m},2\mathrm{m}) $
答案:C
解析:设小球经过时间 $ t $ 打在曲面上的点 $ M(x^\prime ,y^\prime ) $ ,由平抛运动规律得 $ x^\prime ={v}_{0}t $ , $ 6\mathrm{m}-y^\prime =\dfrac{1}{2}g{t}^{2} $ ,又因为 $ y^\prime =x{\prime }^{2} $ ,联立解得 $ x^\prime =1\mathrm{m} $ , $ y^\prime =1\mathrm{m} $ , $ \mathrm{C} $ 正确.
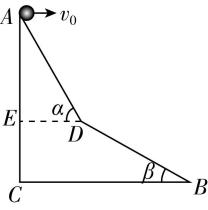
2.如图所示,斜坡由 $ AD $ 和 $ DB $ 两个斜面组成,其中 $ AD $ 与水平面夹角为 $ \alpha ={60}^{\circ } $ , $ DB $ 与水平面夹角为 $ \beta ={30}^{\circ } $ , $ AC=BC $ ,两小球从顶点 $ A $ 以不同大小的初速度沿水平方向抛出,则以下说法正确的是( )
 (多选)
(多选)
A.两球均落在 $ AD $ 面时,速度方向相同
B.两球均落在 $ DB $ 面时,速度方向相同
C.小球落在 $ B $ 点时,速度与水平方向夹角的正切值为 $ \dfrac{2\sqrt{3}}{3} $
D.小球落在 $ D $ 点时,速度与水平方向夹角的正切值为 $ 2\sqrt{3} $
答案:AD
解析:两球均落在 $ AD $ 面时,两球的位移与水平方向的夹角相同,都为 $ {60}^{\circ } $ ,由平抛运动的推论可知,若位移与水平方向的夹角相同,则速度与水平方向的夹角也相同,而若两球均落在 $ DB $ 面上不同位置时,顶点 $ A $ 与两落点的连线与水平方向的夹角不同,则速度与水平方向的夹角也不同,速度方向不同,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;由 $ AC=BC $ 可知,小球落在 $ B $ 点时,位移与水平方向的夹角为 $ {45}^{\circ } $ ,则其正切值为 $ \tan {45}^{\circ }=1 $ ,速度与水平方向的夹角的正切值为2,故 $ \mathrm{C} $ 错误;小球落在 $ D $ 点时,位移与水平方向夹角的正切值为 $ \tan {60}^{\circ }=\sqrt{3} $ ,则速度与水平方向夹角的正切值为 $ 2\sqrt{3} $ ,故 $ \mathrm{D} $ 正确.
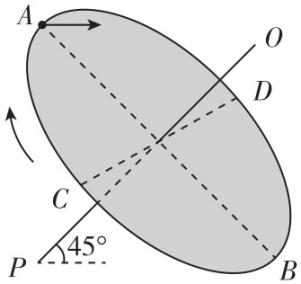
3.如图所示,圆盘绕过中心且垂直圆盘平面的轴 $ OP $ 以周期 $ T $ 匀速转动,轴 $ OP $ 与水平方向夹角为 $ {45}^{\circ } $ ,沿 $ OP $ 方向看,圆盘顺时针转动, $ AB $ 与 $ CD $ 是圆盘上相互垂直的两条直径,当 $ A $ 点刚好过最高点时,一小球从 $ A $ 点相对于地面以某一初速度沿水平方向抛出,经过一个周期 $ T $ (圆盘转一圈所用的时间),小球恰好落在 $ B $ 点,已知重力加速度大小为 $ g $ ,不计空气阻力,则下列说法正确的是( )
 (多选)
(多选)
A.小球的初速度大小为 $ \dfrac{1}{2}gT $ ,圆盘半径为 $ \dfrac{\sqrt{2}}{4}g{T}^{2} $
B.小球的初速度大小为 $ \dfrac{\sqrt{2}}{2}gT $ ,圆盘半径为 $ \dfrac{\sqrt{2}}{4}g{T}^{2} $
C.小球落在 $ B $ 点之前某时刻,速度方向与圆盘上 $ C $ 点的速度方向相同
D.小球落在 $ B $ 点之前某时刻,速度方向与圆盘上 $ D $ 点的速度方向相同
答案:AC
解析:小球做平抛运动,竖直方向为自由落体运动,由几何关系可得 $ vT=\dfrac{1}{2}g{T}^{2} $ ,解得小球的初速度大小 $ v=\dfrac{1}{2}gT $ , $ 2R \cos {45}^{\circ }=\dfrac{1}{2}g{T}^{2} $ ,解得圆盘半径 $ R=\dfrac{\sqrt{2}}{4}g{T}^{2} $ , $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;小球速度方向与圆盘平行时,即与水平方向夹角为 $ {45}^{\circ } $ 时才可能与圆盘上某点速度方向相同,对小球有 $ {v}_{y}={v}_{x} $ ,即 $ gt=\dfrac{1}{2}gT $ ,解得 $ t=\dfrac{1}{2}T $ ,此时圆盘转过半圈,可知 $ C $ 点速度方向平行盘面向下, $ D $ 点速度方向平行盘面向上,小球速度方向与圆盘上 $ C $ 点的速度方向相同, $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
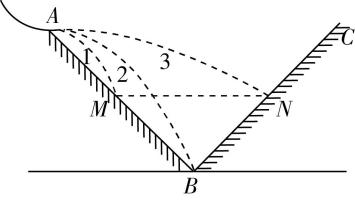
4.如图所示,一小球从加速滑道的不同位置由静止滑下,到达 $ A $ 点后会以不同的速度水平飞出,分别落在坡道的 $ M $ 、 $ B $ 和 $ N $ 点.已知坡道 $ AB $ 和 $ BC $ 的倾角均为 $ {45}^{\circ } $ ,并且 $ M $ 为 $ AB $ 的中点, $ M $ 、 $ N $ 两点在同一水平面上.不计空气阻力,则下列说法正确的是( )
 (多选)
(多选)
A.三次在空中飞行时间之比为 $ 1:2:1 $
B.三次的水平初速度大小之比为 $ 1:\sqrt{2}:3 $
C.落在 $ M $ 点的速度方向和落在 $ B $ 点的速度方向相同
D.落在 $ N $ 点时的速度方向恰好垂直斜坡 $ BC $
答案:BC
解析:根据题意结合几何关系可得,三次的水平位移之比为 $ {x}_{1}:{x}_{2}:{x}_{3}=1:2:3 $ ,竖直位移之比为 $ {y}_{1}:{y}_{2}:{y}_{3}=1:2:1 $ ,根据 $ y=\dfrac{1}{2}g{t}^{2} $ 可知,三次小球在空中飞行时间之比为 $ {t}_{1}:{t}_{2}:{t}_{3}=1:\sqrt{2}:1 $ ,根据 $ x={v}_{0}t $ 可知,水平初速度大小之比为 $ {v}_{01}:{v}_{02}:{v}_{03}=1:\sqrt{2}:3 $ , $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;根据平抛运动的推论,速度与水平方向夹角的正切值等于位移与水平方向夹角正切值的2倍,当小球落在 $ M $ 点和 $ B $ 点时,位移与水平方向的夹角相同,所以速度方向也相同, $ \mathrm{C} $ 正确;当小球落在 $ N $ 点时,设速度方向与水平方向的夹角为 $ \alpha $ ,有 $ \tan \alpha =\dfrac{g{t}_{3}}{{v}_{03}}=\dfrac{g{t}_{1}}{3{v}_{01}}=\dfrac{1}{3}×2 \tan {45}^{\circ }=\dfrac{2}{3} $ ,由此可知,小球落在 $ N $ 点时的速度方向与斜坡 $ BC $ 不垂直, $ \mathrm{D} $ 错误.
5.如图所示,竖直平面内的圆环, $ ab $ 为水平直径, $ cd $ 为另一条直径,一个小球(可以看成质点)在 $ c $ 点以水平向右的初速度 $ {v}_{0}=2\mathrm{m}/\mathrm{s} $ 抛出,刚好落在 $ d $ 点,已知直径 $ ab $ 与直径 $ cd $ 的夹角 $ \theta ={37}^{\circ } $ , $ \sin {37}^{\circ }=0.6 $ , $ \cos {37}^{\circ }=0.8 $ , $ g=10\mathrm{m}/{\mathrm{s}}^{2} $ ,不计空气阻力,则( )
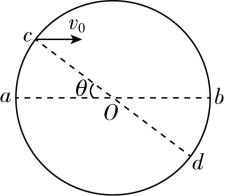
A.圆环的半径为 $ 0.375\mathrm{m} $
B.抛出点 $ c $ 距水平直径 $ ab $ 的高度为 $ 0.45\mathrm{m} $
C.若小球从 $ c $ 点以不同的速度水平向右抛出,一定不能垂直落在圆环上
D.若小球从 $ c $ 点以不同的速度水平向右抛出,经过直径 $ cd $ 上不同位置时的速度方向不相同
答案:A
解析:小球做平抛运动的轨迹如图甲所示,设小球抛出后经过 $ t $ 时间落在 $ d $ 点,根据平抛运动规律有 $ y=\dfrac{1}{2}g{t}^{2} $ , $ x={v}_{0}t $ ,根据几何知识有 $ \dfrac{y}{x}= \tan \theta $ ,联立解得 $ x=0.6\mathrm{m} $ , $ y=0.45\mathrm{m} $ ,则圆环的半径为 $ R=\dfrac{x}{2 \cos \theta }=0.375\mathrm{m} $ ,抛出点 $ c $ 距水平直径 $ ab $ 的高度为 $ ℎ=\dfrac{y}{2}=0.225\mathrm{m} $ ,若小球从 $ c $ 点以不同的速度水平向右抛出,无论经过 $ cd $ 上的何处,其位移与水平方向的夹角均为 $ \theta $ ,则有 $ \tan \theta =\dfrac{y}{x}=\dfrac{gt\prime }{2v} $ ,设速度与水平方向的夹角为 $ \alpha $ ,则有 $ \tan \alpha =\dfrac{{v}_{y}}{v}=\dfrac{gt\prime }{v} $ ,则 $ \tan \alpha =2 \tan \theta $ ,可知 $ \alpha $ 为定值,若小球从 $ c $ 点以不同的速度水平向右抛出,经过直径 $ cd $ 上不同位置时的速度方向相同, $ \mathrm{A} $ 正确, $ \mathrm{B} $ 、 $ \mathrm{D} $ 错误;若小球从 $ c $ 点水平向右抛出垂直落在圆环上 $ f $ 点,如图乙所示,则 $ f $ 点速度反向延长线过圆心,由平抛运动的特点可知速度反向延长线过水平位移的中点 $ g $ ,由图乙可知, $ g $ 点可以为水平位移的中点,故小球可能垂直落在圆环上, $ \mathrm{C} $ 错误.
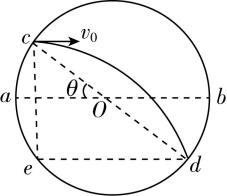
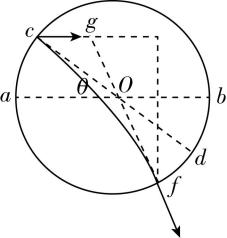
甲 乙


 (多选)
(多选) (多选)
(多选) (多选)
(多选)
 (多选)
(多选) (多选)
(多选) (多选)
(多选)

