第1~2节综合训练
一、刷综合
1.如图所示,乒乓球从斜面滚下后,以某一速度在水平桌面上做直线运动.在与乒乓球路径垂直的方向上放一个直径略大于乒乓球的纸筒.当乒乓球经过纸筒正前方时,用吸管对着球横向吹气.下列说法正确的是( )
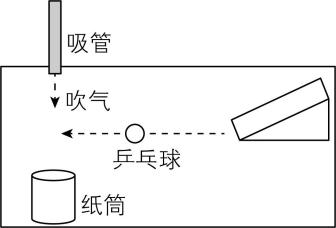
A.乒乓球仍沿着直线运动
B.乒乓球将偏离原来的运动路径,但不进入纸筒
C.乒乓球一定能进入纸筒
D.只有用力吹气,乒乓球才能进入纸筒
答案:B
解析:当乒乓球经过纸筒正前方时,对着乒乓球横向吹气,乒乓球所受合力的方向与速度方向不在同一条直线上,乒乓球做曲线运动,故乒乓球会偏离原来的运动路径;乒乓球会获得一个横向的速度,此速度与乒乓球原来的速度合成一个斜向左下方的合速度,因此乒乓球将向左下方运动,不会进入纸筒, $ \mathrm{A} $ 、 $ \mathrm{C} $ 、 $ \mathrm{D} $ 错误, $ \mathrm{B} $ 正确.
2.如图所示为粉笔在黑板上留下的轨迹,下列说法正确的是( )
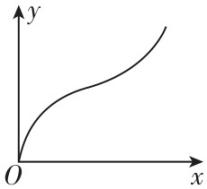 (多选)
(多选)
A.若粉笔沿 $ x $ 轴正方向做匀速直线运动,那么粉笔沿 $ y $ 轴正方向先做加速直线运动后做减速直线运动
B.若粉笔沿 $ x $ 轴正方向做匀速直线运动,那么粉笔沿 $ y $ 轴正方向先做减速直线运动后做加速直线运动
C.若粉笔沿 $ y $ 轴正方向做匀速直线运动,那么粉笔沿 $ x $ 轴正方向先做加速直线运动后做减速直线运动
D.若粉笔沿 $ y $ 轴正方向做匀速直线运动,那么粉笔沿 $ x $ 轴正方向先做减速直线运动后做加速直线运动
答案:BC
解析:做曲线运动的物体,轨迹上某一点的切线方向为该点的速度方向,设某一时刻的速度方向和 $ x $ 轴正方向的夹角为 $ \theta $ ,此时粉笔沿 $ x $ 轴正方向的分速度为 $ {v}_{x} $ ,粉笔沿 $ y $ 轴正方向的分速度为 $ {v}_{y} $ ,则 $ {v}_{y}={v}_{x} \tan \theta $ ,若 $ {v}_{x} $ 不变, $ \theta $ 先减小后增大, $ \tan \theta $ 先减小后增大, $ {v}_{y} $ 先减小后增大,即若粉笔沿 $ x $ 轴正方向做匀速直线运动,那么粉笔沿 $ y $ 轴正方向先做减速直线运动后做加速直线运动, $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;由 $ {v}_{x}=\dfrac{{v}_{y}}{ \tan \theta } $ 知,若 $ {v}_{y} $ 不变, $ \theta $ 先减小后增大, $ \tan \theta $ 先减小后增大, $ {v}_{x} $ 先增大后减小,即若粉笔沿 $ y $ 轴正方向做匀速直线运动,那么粉笔沿 $ x $ 轴正方向先做加速直线运动后做减速直线运动, $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
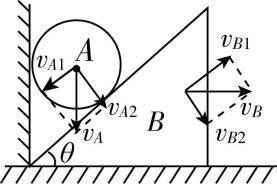
3.如图所示,将楔形木块 $ B $ 靠墙放在光滑水平面上并用手扶着,然后在木块和墙面之间放入一个小球 $ A $ ,楔形木块的倾角为 $ \theta $ ,放手让小球 $ A $ 和木块 $ B $ 同时由静止开始运动,某时刻二者速度大小分别为 $ {v}_{A} $ 和 $ {v}_{B} $ ,则 $ {v}_{A}:{v}_{B} $ 等于( )
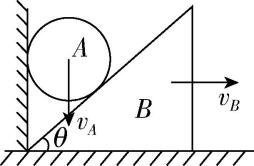
A. $ 1:1 $
B. $ \tan \theta :1 $
C. $ 1: \tan \theta $
D. $ \cos \theta :1 $
答案:B
解析:因为小球A和木块B总是相互接触的,所以小球A的速度 $ {v}_{A} $ 和木块B的速度 $ {v}_{B} $ 在垂直于接触面的方向上的分速度相等,将 $ {v}_{A} $ 、 $ {v}_{B} $ 沿接触面和垂直于接触面的方向进行分解,如图所示,有 $ {v}_{A} \cos \theta ={v}_{B} \sin \theta $ ,可得 $ {v}_{A}:{v}_{B}= \tan \theta :1 {\rm ,B} $ 正确.
4.如图甲所示,直升机放下绳索吊起被困人员,一边收缩绳索一边飞向安全地带.前4秒内被困人员水平方向的 $ {v}_{x}-t $ 图像和竖直方向的 $ {v}_{y}-t $ 图像分别如图乙、丙所示.不计空气阻力,则在这4秒内( )
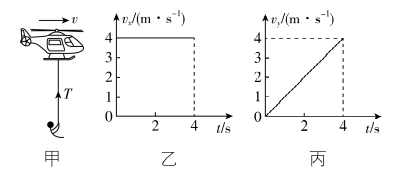 (多选)
(多选)
A.以地面为参考系,被困人员的运动轨迹是一条抛物线
B.以地面为参考系,被困人员的运动轨迹是一条直线
C.人对绳索的拉力大小等于绳索对人的拉力大小
D.以地面为参考系, $ t=4\mathrm{s} $ 时被困人员的速度大小为 $ 4\sqrt{2}\mathrm{m}/\mathrm{s} $
答案:ACD
解析:由题图乙可知,在水平方向上被困人员做匀速直线运动,由题图丙可知,在竖直方向上被困人员向上做匀加速直线运动,以地面为参考系,有 $ x={v}_{0}t $ , $ y=\dfrac{1}{2}a{t}^{2} $ ,联立可得 $ y=\dfrac{a}{2{v}_{0}^{2}}{x}^{2} $ ,所以被困人员的运动轨迹是一条抛物线,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;人对绳索的拉力与绳索对人的拉力是一对相互作用力,大小相等,故 $ \mathrm{C} $ 正确;以地面为参考系, $ t=4\mathrm{s} $ 时被困人员的速度大小为 $ v=\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}=\sqrt{{4}^{2}+{4}^{2}}\mathrm{m}/\mathrm{s}=4\sqrt{2}\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{D} $ 正确.
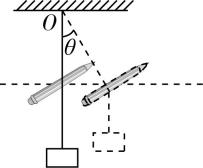
5.如图所示,一块橡皮用细绳悬挂于 $ O $ 点,现用一支铅笔贴着细绳的左侧水平向右以速度 $ {v}_{0} $ 匀速移动,运动过程中保持铅笔的高度不变,悬挂橡皮的那段细绳始终保持竖直.当细绳与竖直方向夹角为 $ \theta ={30}^{\circ } $ 时,橡皮的速度大小为( )
A. $ \dfrac{\sqrt{5}}{2}{v}_{0} $
B. $ 2{v}_{0} $
C. $ {v}_{0} $
D. $ \dfrac{{v}_{0}}{2} $
答案:A
解析:橡皮的运动可以分解为竖直方向沿绳的运动和水平方向的匀速直线运动,将铅笔与绳子接触的点的速度沿倾斜绳方向和垂直于倾斜绳方向分解,如图所示,则沿倾斜绳方向上的分速度大小为 $ {v}_{绳}={v}_{0} \sin \theta =\dfrac{{v}_{0}}{2} $ ,即橡皮在竖直方向上的速度大小为 $ {v}_{y}={v}_{绳}=\dfrac{{v}_{0}}{2} $ ,水平方向的速度大小为 $ {v}_{0} $ ,则橡皮的合速度大小为 $ v=\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}=\dfrac{\sqrt{5}}{2}{v}_{0} $ , $ \mathrm{A} $ 正确.
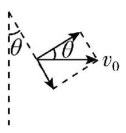
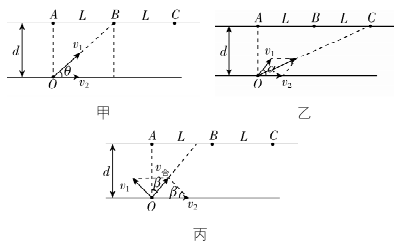
6.如图所示,一船在静水中的速度大小恒定,水流速度大小恒定且方向沿着河岸向右,小船的速度小于水流速度,河岸宽度恒定为 $ d $ .小船从 $ O $ 点开始渡河,图中 $ OA $ 垂直于河岸, $ AB=BC=L $ .已知当小船划行方向垂直于河岸时,小船正好航行到 $ B $ 点,运动时间为 $ {t}_{B} $ ,且 $ d < L $ .则( )
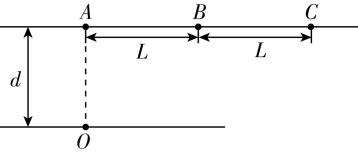
A.小船速度大小与水流速度大小之比为 $ \dfrac{L}{d} $
B.若小船的划行方向沿 $ OB $ ,则小船最终会航行到 $ BC $ 之间的某一点
C.若小船改变划行方向,最终到达对岸 $ C $ 点,运动时间为 $ 2{t}_{B} $
D.若小船改变划行方向,离 $ A $ 点最近的距离为 $ \sqrt{{L}^{2}-{d}^{2}} $
答案:D
解析:设小船速度大小为 $ {v}_{1} $ ,水流速度大小为 $ {v}_{2} $ ,小船划行方向垂直于河岸,航行到 $ B $ 点时有 $ {t}_{B}=\dfrac{d}{{v}_{1}}=\dfrac{L}{{v}_{2}} $ ,则小船速度大小与水流速度大小之比为 $ \dfrac{{v}_{1}}{{v}_{2}}=\dfrac{d}{L} $ , $ \mathrm{A} $ 错误;小船的划行方向沿 $ OB $ 方向时,设 $ {v}_{1} $ 与河岸的夹角为 $ \theta $ ,如图甲所示,则 $ \tan \theta =\dfrac{d}{L} $ , $ \sin \theta =\dfrac{d}{\sqrt{{d}^{2}+{L}^{2}}} $ , $ \cos \theta =\dfrac{L}{\sqrt{{d}^{2}+{L}^{2}}} $ ,此时过河时间 $ {t}_{1}=\dfrac{d}{{v}_{1} \sin \theta }=\dfrac{\sqrt{{d}^{2}+{L}^{2}}}{{v}_{1}} $ ,沿河岸方向的位移大小 $ {x}_{1}=({v}_{2}+{v}_{1} \cos \theta ){t}_{1}=\dfrac{d+\sqrt{{d}^{2}+{L}^{2}}}{d}L > 2L $ ,故小船最终会航行到 $ C $ 点右侧某位置, $ \mathrm{B} $ 错误;小船最终到达对岸 $ C $ 点时,设 $ {v}_{1} $ 与河岸的夹角为 $ \alpha $ ,如图乙所示,则有 $ \dfrac{{v}_{1} \sin \alpha }{{v}_{1} \cos \alpha +{v}_{2}}=\dfrac{d}{2L} $ ,可得 $ \sin \alpha =\dfrac{d \cos \alpha }{2L}+\dfrac{1}{2} > \dfrac{1}{2} $ ,则小船运动到河对岸的时间 $ {t}_{C}=\dfrac{d}{{v}_{1} \sin \alpha } < \dfrac{d}{{v}_{1}\cdot \dfrac{1}{2}}=2{t}_{B} $ , $ \mathrm{C} $ 错误;当小船划行的方向与合速度方向垂直时,小船到达对岸的位置离 $ A $ 点最近,如图丙所示, $ \cos \beta =\dfrac{{v}_{1}}{{v}_{2}}=\dfrac{d}{L} $ ,则 $ \tan \beta =\dfrac{\sqrt{{L}^{2}-{d}^{2}}}{d} $ ,离 $ A $ 点最近的距离为 $ {x}_{2}=d \tan \beta =\sqrt{{L}^{2}-{d}^{2}} $ , $ \mathrm{D} $ 正确.
7.质量 $ m=3\mathrm{k}\mathrm{g} $ 的质点,静止在 $ O $ 点,且以 $ O $ 点为坐标原点建立一直角坐标系, $ t=0 $ 时刻在质点上施加一沿 $ x $ 轴正方向的外力 $ {F}_{x}=6\mathrm{N} $ , $ {t}_{1}=2\mathrm{s} $ 时不改变外力的大小,仅将外力的方向变为沿 $ y $ 轴正方向,再经过 $ {t}_{2}=2\mathrm{s} $ 的时间撤走外力.则下列说法中正确的是( )
 (多选)
(多选)
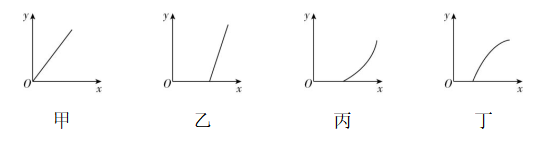
A.质点的运动轨迹可能如图甲所示
B. $ 4\mathrm{s} $ 末质点的坐标为 $ (12\mathrm{m},4\mathrm{m}) $
C. $ 2\sim 4\mathrm{s} $ 内质点的位移大小为 $ 4\mathrm{m} $
D. $ 4\mathrm{s} $ 末质点的速度大小为 $ 4\sqrt{2}\mathrm{m}/\mathrm{s} $
答案:BD
解析:由题可知,质点在前 $ 2\mathrm{s} $ 内由静止开始沿 $ x $ 轴正方向做匀加速直线运动, $ 2\sim 4\mathrm{s} $ 内,质点沿 $ y $ 轴正方向做初速度为零的匀加速直线运动,而沿 $ x $ 轴正方向,质点做匀速直线运动,故其轨迹可能如题图丙所示,故 $ \mathrm{A} $ 错误.由牛顿第二定律可知,在 $ x $ 轴正方向质点获得的加速度大小 $ {a}_{1}=\dfrac{{F}_{x}}{m}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,故在前 $ 2\mathrm{s} $ 内沿 $ x $ 轴的位移大小 $ {x}_{1}=\dfrac{1}{2}{a}_{1}{t}_{1}^{2}=4\mathrm{m} $ , $ 2\mathrm{s} $ 末的速度大小 $ v={a}_{1}{t}_{1}=4\mathrm{m}/\mathrm{s} $ ; $ 2\sim 4\mathrm{s} $ 内沿 $ x $ 轴正方向做匀速直线运动,故沿 $ x $ 轴的位移大小 $ {x}_{2}=v{t}_{2}=8\mathrm{m} $ ,则其沿 $ x $ 轴正方向移动的距离 $ x={x}_{1}+{x}_{2}=12\mathrm{m} $ ; $ 2\sim 4\mathrm{s} $ 内,在 $ y $ 轴正方向质点获得的加速度大小 $ {a}_{2}=\dfrac{{F}_{y}}{m}=2\mathrm{m}/{\mathrm{s}}^{2} $ ,故 $ 2\sim 4\mathrm{s} $ 内沿 $ y $ 轴正方向的位移大小 $ y=\dfrac{1}{2}{a}_{2}{t}_{2}^{2}=4\mathrm{m} $ ,故 $ 4\mathrm{s} $ 末质点的坐标为 $ (12\mathrm{m},4\mathrm{m}) $ ,故 $ \mathrm{B} $ 正确.由以上分析可知, $ 2\sim 4\mathrm{s} $ 内质点的位移大小 $ s=\sqrt{{4}^{2}+{8}^{2}}\mathrm{m}=4\sqrt{5}\mathrm{m} $ ,故 $ \mathrm{C} $ 错误.由以上分析可知, $ 4\mathrm{s} $ 末质点沿 $ y $ 轴正方向的速度大小为 $ {v}_{y}={a}_{2}{t}_{2}=4\mathrm{m}/\mathrm{s} $ ,由速度的合成可得, $ 4\mathrm{s} $ 末质点的速度大小 $ {v}_{4}=\sqrt{{4}^{2}+{4}^{2}}\mathrm{m}/\mathrm{s}=4\sqrt{2}\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{D} $ 正确.
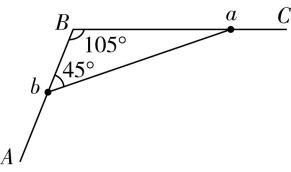
8.如图所示,粗细均匀的直杆 $ AB $ 、 $ BC $ 连接固定在竖直面内, $ \mathrm{\angle }ABC={105}^{\circ } $ , $ a $ 、 $ b $ 两球分别套在 $ AB $ 、 $ BC $ 杆上,用细线连接,给 $ a $ 球施加一个拉力,使 $ a $ 球沿 $ BC $ 杆向右运动,当细线与 $ AB $ 杆的夹角为 $ {45}^{\circ } $ 时, $ a $ 、 $ b $ 两球的速度大小之比为( )
A. $ \sqrt{2}:\sqrt{3} $
B. $ \sqrt{3}:\sqrt{2} $
C. $ 1:\sqrt{2} $
D. $ \sqrt{2}:1 $
答案:A
解析:将 $ a $ 、 $ b $ 两球的速度沿细线方向( $ x $ 方向)和垂直于细线方向分解可得 $ {v}_{ax}={v}_{a} \cos {30}^{\circ }=\dfrac{\sqrt{3}}{2}{v}_{a} $ , $ {v}_{bx}={v}_{b} \cos {45}^{\circ }=\dfrac{\sqrt{2}}{2}{v}_{b} $ ,由绳关联速度知识可知 $ {v}_{ax}={v}_{bx} $ ,则 $ a $ 、 $ b $ 两球的速度大小之比为 $ \dfrac{{v}_{a}}{{v}_{b}}=\dfrac{\sqrt{2}}{\sqrt{3}} $ ,故选 $ \mathrm{A} $ .
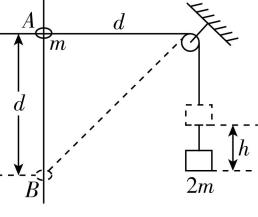
9.如图所示,将质量为 $ 2m $ 的重物悬挂在轻绳的一端,轻绳的另一端系一质量为 $ m $ 的小环,小环套在竖直固定的光滑直杆上,光滑定滑轮与直杆间的距离为 $ d $ .现将小环从与定滑轮等高的 $ A $ 处由静止释放,当小环沿直杆下滑距离也为 $ d $ 时(图中 $ B $ 处),则(重力加速度为 $ g $ )( )
A.小环刚释放时轻绳中的张力一定小于 $ 2mg $
B.小环到达 $ B $ 处时,重物上升的高度 $ h=d $
C.在小环从 $ A $ 下滑到 $ B $ 的过程中,小环的速度与重物上升的速度的比值逐渐增大
D.小环在 $ B $ 处的速度与重物上升的速度大小之比等于 $ \sqrt{2} $
答案:D
解析:小环由静止释放时,重物即将向上加速,对重物由牛顿第二定律得 $ T-2mg=2ma $ ,则轻绳中的张力一定大于 $ 2mg $ ,故 $ \mathrm{A} $ 错误;小环到达 $ B $ 处时,定滑轮左侧轻绳增大的长度等于重物上升的高度,有 $ h=\sqrt{2}d-d $ ,故 $ \mathrm{B} $ 错误;设轻绳与直杆的夹角为 $ \theta $ ,在小环从 $ A $ 下滑到 $ B $ 的过程中,小环沿绳方向的速度与重物上升的速度大小相等,有 $ {v}_{环} \cos \theta ={v}_{物} $ ,则小环的速度与重物上升的速度之比 $ \dfrac{{v}_{环}}{{v}_{物}}=\dfrac{1}{ \cos \theta } $ ,随着小环下落, $ \theta $ 减小,故比值减小,故 $ \mathrm{C} $ 错误;小环在 $ B $ 处时轻绳与直杆的夹角为 $ {45}^{\circ } $ ,此时小环的速度与重物上升的速度大小之比 $ \dfrac{{v}_{环}}{{v}_{物}}=\dfrac{1}{ \cos {45}^{\circ }}=\sqrt{2} $ ,故 $ \mathrm{D} $ 正确.
10.各种大型的货运站中少不了悬臂式起重机.如图甲所示,某起重机的悬臂保持不动,可沿悬臂行走的天车有两个功能,一是吊着货物沿竖直方向运动,二是吊着货物沿悬臂水平方向运动.现天车吊着质量为 $ 100\mathrm{k}\mathrm{g} $ 的货物在 $ x $ 方向的位移—时间图像和 $ y $ 方向的速度—时间关系图像如图乙、丙所示,下列说法正确的是( )
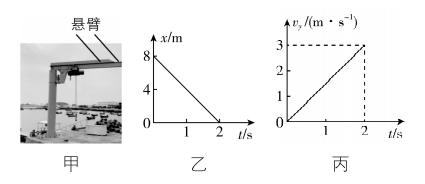
A. $ t=2\mathrm{s} $ 时货物的速度大小为 $ 3\mathrm{m}/\mathrm{s} $
B.货物的运动轨迹是一条直线
C.货物所受的合力大小为 $ 150\mathrm{N} $
D. $ 0\sim 2\mathrm{s} $ 这段时间内,货物的合位移大小为 $ 11\mathrm{m} $
答案:C
解析:由题图乙可知货物在水平方向做匀速直线运动,速度大小为 $ {v}_{x}=\dfrac{8}{2}\mathrm{m}/\mathrm{s}=4\mathrm{m}/\mathrm{s} $ ,由题图丙可知货物在竖直方向做初速度为0的匀加速直线运动, $ 2\mathrm{s} $ 末货物的竖直分速度大小为 $ 3\mathrm{m}/\mathrm{s} $ ,则 $ t=2\mathrm{s} $ 时货物的速度大小为 $ v=\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}=\sqrt{{4}^{2}+{3}^{2}}\mathrm{m}/\mathrm{s}=5\mathrm{m}/\mathrm{s} $ ,货物的合运动为匀变速曲线运动,运动轨迹是一条抛物线, $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;根据题图丙可知,货物的加速度大小为 $ a=\dfrac{\mathrm{\Delta }{v}_{y}}{\mathrm{\Delta }t}=\dfrac{3-0}{2-0}\mathrm{m}/{\mathrm{s}}^{2}=1.5\mathrm{m}/{\mathrm{s}}^{2} $ ,根据牛顿第二定律可得合力大小为 $ F=ma=100×1.5\mathrm{N}=150\mathrm{N} $ , $ \mathrm{C} $ 正确;由题图乙可知 $ 0\sim 2\mathrm{s} $ 这段时间内,货物的水平位移大小为 $ x=8\mathrm{m} $ ,货物的竖直位移大小为 $ y=\dfrac{2×3}{2}\mathrm{m}=3\mathrm{m} $ ,则合位移大小为 $ s=\sqrt{{x}^{2}+{y}^{2}}=\sqrt{{8}^{2}+{3}^{2}}\mathrm{m}=\sqrt{73}\mathrm{m} $ , $ \mathrm{D} $ 错误.

 (多选)
(多选)

 (多选)
(多选)



 (多选)
(多选)

