专题2 关联速度
一、刷题型
1.如图所示,光滑水平面上固定两个光滑立柱 $ A $ 和 $ B $ ,两根柔软轻绳对称地跨过两立柱,每根绳的一端系在物体上的 $ O $ 点,另一端施加沿绳方向的等大外力,使物体能沿两绳夹角的角平分线运动,物体质量为 $ m $ .当绳子之间夹角为 $ 2\alpha $ 时,绳端速度大小为 $ v $ ,拉力大小为 $ F $ ,此时物体的速度大小 $ {v}_{物} $ 和加速度大小 $ {a}_{物} $ 表达式正确的是( )
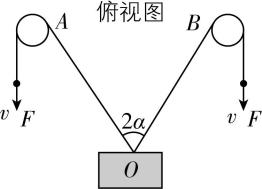
A. $ {v}_{物}=\dfrac{2v}{ \cos \alpha } $
B. $ {v}_{物}=2v \cos \alpha $
C. $ {a}_{物}=\dfrac{2F}{m \cos \alpha } $
D. $ {a}_{物}=\dfrac{2F \cos \alpha }{m} $
答案:D
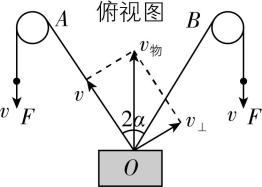
解析:把物体的速度分解为沿绳方向和垂直于绳方向,对左边的绳子,画出物体的速度分解图,如图所示,则 $ {v}_{物}=\dfrac{v}{ \cos \alpha } $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;根据牛顿第二定律有 $ 2F \cos \alpha =m{a}_{物} $ ,解得 $ {a}_{物}=\dfrac{2F \cos \alpha }{m} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
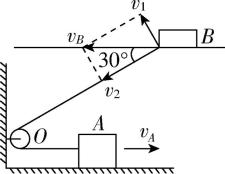
2.如图所示,有两条位于同一竖直平面内的水平轨道,轨道上有两个物体 $ A $ 和 $ B $ ,它们通过一根绕过定滑轮 $ O $ 的不可伸长的轻绳相连接,物体 $ A $ 以速度 $ {v}_{A}=20\mathrm{m}/\mathrm{s} $ 匀速向右运动,在绳子与轨道成 $ \alpha ={30}^{\circ } $ 角时,物体 $ B $ 的速度大小 $ {v}_{B} $ 为( )
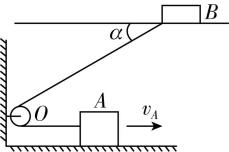
A. $ 10\sqrt{3}\mathrm{m}/\mathrm{s} $
B. $ \dfrac{40\sqrt{3}}{3}\mathrm{m}/\mathrm{s} $
C. $ 40\mathrm{m}/\mathrm{s} $
D. $ 10\mathrm{m}/\mathrm{s} $
答案:B
解析:将 $ B $ 的速度沿绳方向和垂直绳方向分解,如图所示,则有 $ {v}_{2}={v}_{A} $ , $ {v}_{2}={v}_{B} \cos {30}^{\circ } $ ,解得 $ {v}_{B}=\dfrac{{v}_{A}}{ \cos {30}^{\circ }}=\dfrac{40\sqrt{3}}{3}\mathrm{m}/\mathrm{s} $ ,故 $ \mathrm{B} $ 正确.
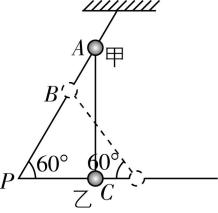
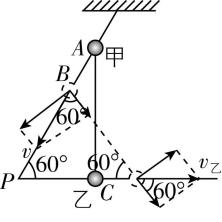
3.如图所示,“ $ \mathrm{\angle } $ ”形光滑硬杆固定在竖直平面内, $ \mathrm{\angle }P={60}^{\circ } $ ,底边水平.均可视为质点的带孔小球甲、乙间用轻质细杆相连,分别套在“ $ \mathrm{\angle } $ ”形杆上的 $ A $ 、 $ C $ 点,开始时两球在同一竖直线上处于静止状态,某时刻给乙球一个向右的轻微扰动使它们开始运动,当甲球运动到 $ B $ 点时,速度大小为 $ v $ ,轻质细杆与水平方向的夹角为 $ {60}^{\circ } $ ,则此时乙球的速度大小为( )
A. $ \dfrac{v}{2} $
B. $ v $
C. $ \sqrt{3}v $
D. $ 2v $
答案:B
解析:如图所示,当甲球运动到 $ B $ 点时,速度大小为 $ v $ ,轻质细杆与水平方向的夹角为 $ {60}^{\circ } $ ,设此时乙球的速度大小为 $ {v}_{乙} $ ,根据甲、乙两球沿杆方向的分速度大小相等,可得 $ v \cos {60}^{\circ }={v}_{乙} \cos {60}^{\circ } $ ,解得 $ {v}_{乙}=v $ , $ \mathrm{B} $ 正确.
4.曲柄连杆结构是发动机的主要运动结构,其用途是将活塞的往复运动转变为曲轴的旋转运动,同时将作用于活塞上的力转变为曲轴对外输出的转矩,以驱动车轮转动.其结构简化示意图如图所示,曲轴可绕固定的 $ O $ 点自由转动,连杆两端分别连接曲轴上的 $ A $ 点和活塞上的 $ B $ 点.若曲轴绕 $ O $ 点做匀速圆周运动,下列说法正确的是( )
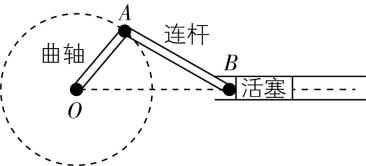
A.活塞在水平方向做匀速直线运动
B.当 $ OA $ 与 $ AB $ 垂直时,若 $ AB $ 与水平方向夹角为 $ \theta $ ,则 $ {v}_{A} \cos \theta ={v}_{B} $
C.当 $ OA $ 与 $ AB $ 共线时, $ A $ 点与 $ B $ 点的速度大小相等
D.当 $ OA $ 与 $ OB $ 垂直时, $ A $ 点与 $ B $ 点的速度大小相等
答案:D
解析:设 $ A $ 点的速度大小为 $ {v}_{A} $ ,当 $ OA $ 与 $ AB $ 垂直时, $ AB $ 与水平方向的夹角为 $ \theta $ ,则 $ {v}_{B} \cos \theta ={v}_{A} $ , $ \mathrm{B} $ 错误;当 $ OA $ 与 $ AB $ 共线时, $ {v}_{A} $ 在沿杆方向的分量为零,此时 $ B $ 点速度为零, $ A $ 点与 $ B $ 点的速度大小不相等, $ \mathrm{C} $ 错误;当 $ OA $ 与 $ OB $ 垂直时,设 $ AB $ 与水平方向的夹角为 $ \alpha $ ,则 $ {v}_{A} \cos \alpha ={v}_{B} \cos \alpha $ ,即 $ {v}_{A}={v}_{B} $ , $ \mathrm{D} $ 正确;根据前面分析可知活塞在水平方向做变速直线运动, $ \mathrm{A} $ 错误.
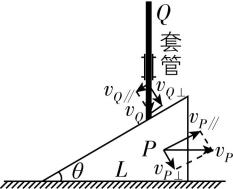
5.如图所示,斜面体 $ P $ 高为 $ H $ 、底边长为 $ L $ ,放在水平光滑地面上.斜面体上方某位置固定一套管,细长直杆 $ Q $ 穿过套管,在套管约束下只能沿竖直方向运动.开始时直杆 $ Q $ 和 $ P $ 刚好接触,释放直杆 $ Q $ 后, $ P $ 沿地面向右运动,则 $ P $ 和 $ Q $ 的速度大小之比为( )
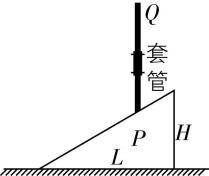
A. $ \dfrac{L}{H} $
B. $ \dfrac{H}{L} $
C. $ \sqrt{\dfrac{L}{H}} $
D. $ \sqrt{\dfrac{H}{L}} $
答案:A
解析:如图所示,设斜面倾角为 $ \theta $ ,直杆和斜面体沿垂直于接触面方向的分速度大小相等,有 $ {v}_{Q} \cos \theta ={v}_{P} \sin \theta $ ,由几何关系得 $ \tan \theta =\dfrac{H}{L} $ ,则 $ \dfrac{{v}_{P}}{{v}_{Q}}=\dfrac{ \cos \theta }{ \sin \theta }=\dfrac{1}{ \tan \theta }=\dfrac{L}{H} $ , $ \mathrm{A} $ 正确.