1．通常情况下，越靠近河岸，河水的流速越小.若一小船从南岸到北岸横渡一条河，小船的静水速度大小、方向均不变（船头方向垂直于河岸），则在下列四幅图中，能表示小船渡河的轨迹的是（ ）
A．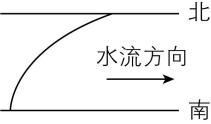
B．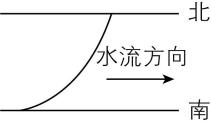
C．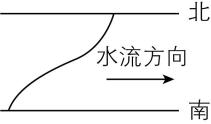
D．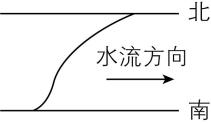
根据题意可知，从南岸到北岸，河水的流速先增大后减小，又小船在垂直河岸方向上做匀速直线运动，故小船的合速度与河岸方向的夹角先减小后增大，结合合速度方向沿运动轨迹的切线方向，可知小船渡河过程中的运动轨迹应先向下游弯曲，后向上游弯曲， $ \mathrm{C} $ 正确.
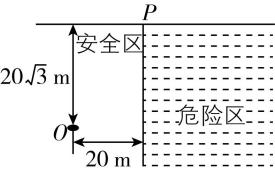
2．我国某款无人艇装上相控阵雷达.如图所示，该无人艇位于与对岸的最近距离为 $ 20\sqrt{3}\mathrm{m} $ 的 $ O $ 点处，从 $ O $ 点向下游 $ 20\mathrm{m} $ 处有一危险区，当时水流速度为 $ 17\sqrt{3}\mathrm{m}/\mathrm{s} $ ，为了使无人艇避开危险区沿直线到达对岸，无人艇在静水中的速度大小至少为（ ）
A． $ 20\mathrm{m}/\mathrm{s} $
B． $ 20\sqrt{3}\mathrm{m}/\mathrm{s} $
C． $ 25.5\mathrm{m}/\mathrm{s} $
D． $ 50\mathrm{m}/\mathrm{s} $
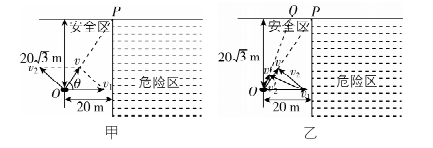
若无人艇刚好避开危险区，如图甲所示，设无人艇沿 $ OP $ 方向以速度 $ v $ 行驶，水流速度为 $ {v}_{1} $ ，由几何知识得 $ \tan \theta =\dfrac{20\sqrt{3}}{20}=\sqrt{3} $ ，所以 $ \theta ={60}^{\circ } $ ，当无人艇在静水中的速度 $ {v}_{2}\perp v $ 时， $ {v}_{2} $ 最小， $ {v}_{2}={v}_{1} \sin \theta =17\sqrt{3}×\dfrac{\sqrt{3}}{2}\mathrm{m}/\mathrm{s}=25.5\mathrm{m}/\mathrm{s} $ ，显然无人艇沿其他方向行驶时，如沿 $ OQ $ 以速度 $ v^\prime $ 行驶时（如图乙所示），在静水中的速度 $ v{\prime }_{2} > {v}_{2} $ ，则无人艇在静水中的速度大小至少为 $ 25.5\mathrm{m}/\mathrm{s} $ ， $ \mathrm{C} $ 正确.
3．一船由河岸的 $ A $ 点出发，经过一段时间到达对岸，已知水速为 $ {v}_{1} $ ，船在静水中的速度为 $ {v}_{2} $ ，两河岸的最近距离为 $ d $ .可认为河水的水面是水平的.则（ ）
A．船到达对岸时的速度一定不等于 $ {v}_{2} $
B．若 $ {v}_{1} > {v}_{2} $ ，船渡河的最小位移为 $ \dfrac{\sqrt{{v}_{1}^{2}+{v}_{2}^{2}}}{{v}_{1}}d $
C．若 $ {v}_{2} > {v}_{1} $ ，且船渡河的位移最短时，船渡河的时间为 $ \dfrac{d}{\sqrt{{v}_{2}^{2}-{v}_{1}^{2}}} $
D．船渡河的最短时间为 $ \dfrac{d}{\sqrt{{v}_{1}^{2}+{v}_{2}^{2}}} $
船到达对岸时的速度为合速度，可能大于、等于或小于船速，故与 $ {v}_{2} $ 的大小关系不确定， $ \mathrm{A} $ 错误；若 $ {v}_{1} > {v}_{2} $ ，则当合速度的方向与船速的方向垂直时，船渡河的位移最短，设此时合速度的方向与河岸夹角为 $ \theta $ ，则有 $ \sin \theta =\dfrac{{v}_{2}}{{v}_{1}} $ ，则渡河的最小位移 $ x=\dfrac{d}{ \sin \theta }=\dfrac{{v}_{1}}{{v}_{2}}d $ ， $ \mathrm{B} $ 错误；若 $ {v}_{2} > {v}_{1} $ ，则当合速度垂直于河岸时，船渡河的位移最短，此时船渡河的时间为 $ t=\dfrac{d}{\sqrt{{v}_{2}^{2}-{v}_{1}^{2}}} $ ， $ \mathrm{C} $ 正确；无论船速与水速的关系如何，欲使船渡河的时间最短，都必须使船头垂直于河岸，渡河的最短时间为 $ t=\dfrac{d}{{v}_{2}} $ ， $ \mathrm{D} $ 错误.
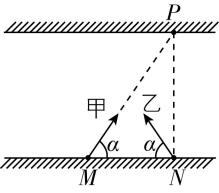
4．如图所示，甲、乙两船从一条河流的同一岸边同时开始渡河，河宽为 $ d $ ， $ M $ 、 $ N $ 分别是甲、乙两船的出发点，其船头与河岸均成 $ \alpha $ 角，甲船船头恰好对准 $ N $ 点的正对岸 $ P $ 点，经过一段时间乙船恰好到达 $ P $ 点，如果两船的速度大小均为 $ {v}_{0} $ ，且两船相遇不影响各自的航行.下列判断正确的是（ ）
（多选）
A．水流方向向左，大小为 $ {v}_{0} \cos \alpha $
B．两船同时到达河对岸，所用时间均为 $ \dfrac{d}{{v}_{0} \sin \alpha } $
C．甲船沿河岸方向的位移大小为 $ \dfrac{d}{ \sin \alpha } $
D．甲、乙两船会在 $ PN $ 上某点相遇
以乙船为研究对象,如果水流方向向左,如图1所示,则船的合速度方向为斜向左上,乙船不可能到达 $ P $ 点,则水流方向一定向右,且依题意可知乙船的合速度垂直河岸,则乙船向左的分速度与水流速度大小相等,可得 $ {v}_{水}={v}_{0} \cos \alpha $ ,故 $ \mathrm{A} $ 错误；两船在垂直水流方向上的速度大小均为 $ {v}_{0} \sin \alpha $ ,且河宽均为 $ d $ ,则两船同时到达河对岸,所用时间均为 $ t=\dfrac{d}{{v}_{0} \sin \alpha } $ ,故 $ \mathrm{B} $ 正确；以甲船为研究对象,水流方向向右,如图2所示,则船在水流方向上的速度大小为 $ {v}_{x}={v}_{水}+{v}_{0} \cos \alpha =2{v}_{0} \cos \alpha $ ,则甲船沿河岸方向的位移大小为 $ x={v}_{x}t=\dfrac{2d}{ \tan \alpha } $ ,故 $ \mathrm{C} $ 错误；甲、乙两船垂直河岸方向上的速度大小均为 $ {v}_{0} \sin \alpha $ ,且这也是乙的合速度,而甲船还有沿水流方向的速度,即两船在垂直河岸方向上相对静止,而沿水流方向上甲船以 $ 2{v}_{0} \cos \alpha $ 的速度靠近乙船,且甲船最终会到达 $ P $ 点右侧某位置，所以甲、乙两船会在 $ PN $ 上某点相遇,故 $ \mathrm{D} $ 正确.
5．假设在某次军事演练时士兵驾驶坦克向东的速度大小为 $ {v}_{1} $ ，坦克静止时射出的炮弹速度大小为 $ {v}_{2}({v}_{2} > {v}_{1}) $ ，且出膛方向沿水平面内可调整，坦克轨迹距离目标最近为 $ d $ ，炮弹飞行时间极短，忽略炮弹受到的空气阻力和炮弹竖直方向的下落高度，且不计炮弹发射对坦克速度的影响.
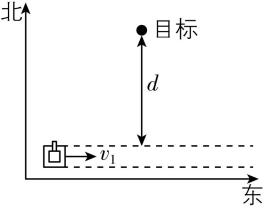
（1） 若要命中目标且炮弹在空中飞行时间最短，最短时间为多少？坦克发射处离目标的距离为多少？
（2） 若到达距离目标最近处时再开炮，求炮弹从发射到命中目标的时间.
（1） $ \dfrac{d}{{v}_{2}} $ ； $ \sqrt{{d}^{2}+{\left(\dfrac{d{v}_{1}}{{v}_{2}}\right) ^ {2}}} $
（2） $ \dfrac{d}{\sqrt{{v}_{2}^{2}-{v}_{1}^{2}}} $
（1） 炮弹向北射出时，炮弹在空中飞行时间最短，则最短时间为 $ {t}_{1}=\dfrac{d}{{v}_{2}} $ ，
坦克发射处离目标的距离为 $ x=\sqrt{{d}^{2}+{\left(\dfrac{d{v}_{1}}{{v}_{2}}\right) ^ {2}}} $ .
（2） 若到达距离目标最近处时再开炮，由于 $ {v}_{2} > {v}_{1} $ ，应调整炮口至北偏西方向可以射中目标，则炮弹从发射到命中目标的时间为 $ {t}_{2}=\dfrac{d}{\sqrt{{v}_{2}^{2}-{v}_{1}^{2}}} $ .