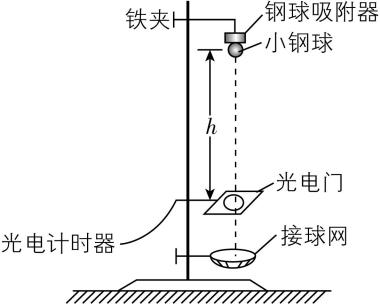
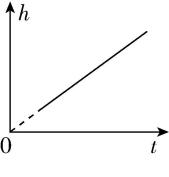
1.【科学探究】某实验小组用如图1所示的装置来测量物块甲与水平桌面间的动摩擦因数.物块甲、乙通过轻质细线连接,轻质细线跨过水平桌面右边缘的定滑轮,甲被控制在桌面上,乙吊在定滑轮的下方,在乙的下方固定一光电门,乙与光电门间的高度差为 $ ℎ $ ,甲、乙的质量相等,乙的上下表面高度差为 $ d(d $ 远小于 $ ℎ) $ .现松开甲,乙向下运动通过光电门的挡光时间为 $ \mathrm{\Delta }t $ ,改变释放时乙与光电门间的高度差 $ ℎ $ ,测出乙通过光电门相应的挡光时间 $ \mathrm{\Delta }t $ ,用测得的数据描绘出 $ \dfrac{1}{{\left(\mathrm{\Delta }t\right) ^ {2}}} $ 与 $ ℎ $ 的关系图像如图2所示,重力加速度为 $ g $ ,回答下列问题:
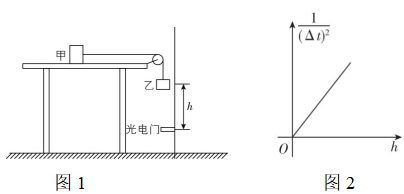
(1) 桌面上方细线与桌面 (填“可以不平行”或“必须平行”),乙通过光电门时的速度大小为 .(用题中所给字母表示)
(2) 细线的拉力 乙的重力,乙的加速度 $ \dfrac{g}{2} $ (均填“大于”“小于”或“等于”).
(3) 若图2的斜率为 $ k $ ,则甲与桌面间的动摩擦因数为 .
(1) 必须平行; $ \dfrac{d}{\mathrm{\Delta }t} $
(2) 小于;小于
(3) $ 1-\dfrac{k{d}^{2}}{g} $
(1) 对甲分析时,需要用细线的拉力减去甲所受摩擦力来表示所受合力,若桌面上方细线与桌面不平行,需要把细线的拉力沿着水平方向和竖直方向分解,因为细线与水平方向的夹角未知,会导致加速度无法求解,则桌面上方细线与桌面必须平行,短时间内可以用平均速度替代瞬时速度,则乙通过光电门的速度为 $ v=\dfrac{d}{\mathrm{\Delta }t} $ .
(2) 甲、乙做匀加速直线运动,乙向下加速,处于失重状态,则细线的拉力小于乙的重力,对甲、乙组成的整体进行受力分析,由牛顿第二定律,可得 $ mg-\mu mg=2ma $ ,可得 $ a=\dfrac{g}{2}-\dfrac{\mu g}{2} < \dfrac{g}{2} $ .
(3) 对乙,由速度—位移关系可得 $ 2aℎ={\left(\dfrac{d}{\mathrm{\Delta }t}\right) ^ {2}} $ ,有 $ \dfrac{1}{(\mathrm{\Delta }t)^{2}}=\dfrac{2a}{{d}^{2}}ℎ $ ,若 $ \dfrac{1}{(\mathrm{\Delta }t)^{2}}-ℎ $ 关系图像的斜率为 $ k $ ,有 $ \dfrac{2a}{{d}^{2}}=k $ ,结合 $ a=\dfrac{g}{2}-\dfrac{\mu g}{2} $ ,联立可得 $ \mu =1-\dfrac{k{d}^{2}}{g} $ .
 B.
B.
 D.
D.
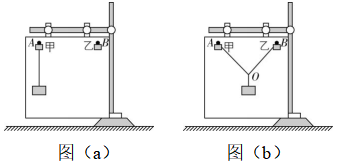
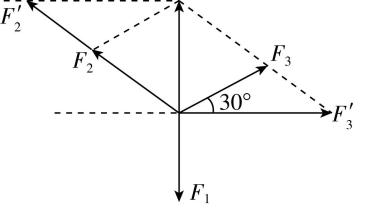
 B.
B.
 D.
D.