第2节 实验：探究加速度与力、质量的关系

一、刷基础

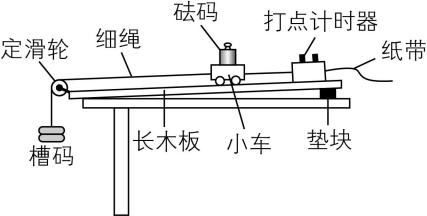
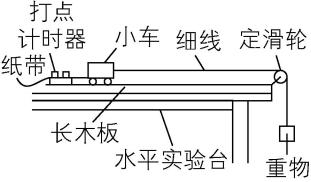
1．某兴趣小组“探究小车加速度与合外力的关系”的实验装置如图甲所示 $ {\rm .} A $ 为小车（质量为 $ M $ ）， $ B $ 为打点计时器， $ C $ 为装有沙的沙桶（沙和沙桶的总质量为 $ m $ ）， $ D $ 为一端带有定滑轮的长木板，电源频率为 $ 50\mathrm{H}\mathrm{z} $ .

试题资源网 https://stzy.com

甲

（1） 下列实验操作中，正确的是     ；

A．调节滑轮的高度，使牵引小车的细绳与长木板保持平行

B．每次实验，都要先放开小车，再接通打点计时器

C．改变小车的质量时，需要重新平衡摩擦力

D．平衡摩擦力时，应将小车后面的纸带连接好

（2） 请简要补充完整平衡摩擦力的操作步骤：用小木板适当垫高长木板不带滑轮的一端，                                      ；

（3） 为使细绳对小车的拉力 $ F $ 近似等于沙和沙桶的总重力，需满足的条件是      ；

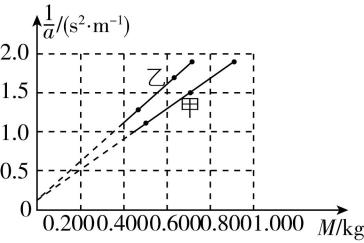
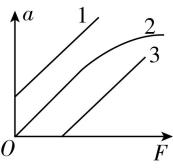
（4） 在本实验中认为细绳的拉力 $ F $ 等于沙和沙桶的总重力，已知三位同学利用实验数据作出的 $ a-F $ 图像如图乙中的1、2、3所示.下列分析正确的是    ；

试题资源网 https://stzy.com

乙

A．出现图线1的原因可能是平衡摩擦力不充分

B．出现图线2弯曲的原因可能是沙和沙桶的质量不合适

C．出现图线3的原因可能是在平衡摩擦力时长木板的倾斜角度过大

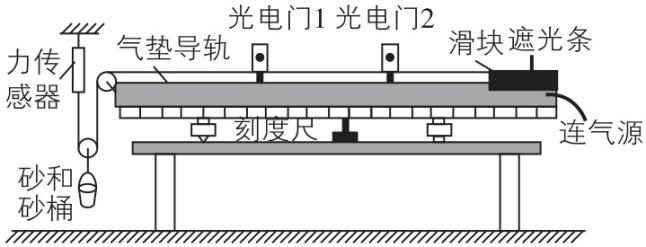
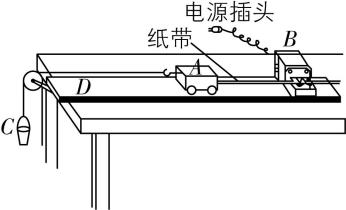
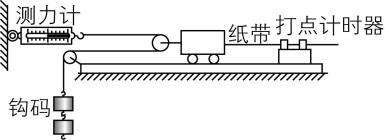
（5） 胡同学改进实验方案，采用图丙的实验装置探究“小车加速度与合外力的关系”时，是否需要平衡摩擦力？  （填“需要”或“不需要”）.

试题资源网 https://stzy.com

丙

答案：

（1） AD

（2） 轻推小车,直到点迹均匀,小车做匀速运动

（3） $ m\ll M $

（4） B

（5） 需要

解析：

（1） 调节滑轮的高度,使牵引小车的细绳与长木板保持平行,保证小车所受的合力方向不变,故 $ \mathrm{A} $ 正确；为了避免纸带上出现大量的空白,实验时,应该先接通电源,后放开小车,故 $ \mathrm{B} $ 错误；由于平衡摩擦力时有 $ Mg \sin \theta =\mu Mg \cos \theta $ ,质量可以约去,所以改变小车的质量时,不需要重新平衡摩擦力,故 $ \mathrm{C} $ 错误；实验中需要平衡的摩擦力是长木板对小车的摩擦力和打点计时器与纸带之间的摩擦力,因此平衡摩擦力时小车后面的纸带必须连好,故 $ \mathrm{D} $ 正确.

（2） 平衡摩擦力的操作步骤：用小木板适当垫高长木板不带滑轮的一端,轻推小车,直到点迹均匀,小车做匀速运动.

（3） 根据牛顿第二定律（下节学习）,对小车,有 $ F=Ma $ ,对沙和沙桶,有 $ mg-F=ma $ ,联立解得 $ F=\dfrac{Mmg}{M+m}=\dfrac{mg}{1+\dfrac{m}{M}} $ ,可知只有当 $ m\ll M $ 时 $ F $ 才近似等于 $ mg $ .

（4） 出现图线1的原因可能是平衡摩擦力时,长木板倾角过大,没有施加拉力时小车就产生加速度,故 $ \mathrm{A} $ 错误；出现图线2的原因可能是沙和沙桶的质量没有远小于小车的质量,小车所受的合外力不等于沙和沙桶的重力,故 $ \mathrm{B} $ 正确；出现图线3的原因可能是平衡摩擦力时,长木板倾角过小,施加一定的拉力时才能使小车产生加速度,故 $ \mathrm{C} $ 错误.

（5） 胡同学的实验方案中,为了使测力计示数的2倍等于小车所受合外力,需要平衡摩擦力.

2．用图1所示实验装置探究加速度与力、质量的关系.

试题资源网 https://stzy.com

图1

（1） 以下操作正确的是    .

A．小车质量应远小于槽码质量

B．拉小车的细绳要平行于长木板

C．补偿阻力时要移去槽码和纸带

D．需要抬高长木板的右侧以补偿阻力

（2） 某次正确操作后获得一条如图2所示的纸带，建立以计数点0为坐标原点的 $ x $ 轴，各计数点的位置坐标分别为0、 $ {x}_{1} $ 、…、 $ {x}_{6} $ .已知打点计时器的打点周期为 $ T $ ，则小车加速度 $ a $ 的表达式是    .

试题资源网 https://stzy.com

图2

A． $ a=\dfrac{{x}_{6}-2{x}_{3}}{{\left(3T\right) ^ {2}}} $ B． $ a=\dfrac{{x}_{6}-2{x}_{3}}{{\left(15T\right) ^ {2}}} $

C． $ a=\dfrac{{x}_{6}+{x}_{5}+{x}_{4}-{x}_{3}-{x}_{2}-{x}_{1}}{{\left(3T\right) ^ {2}}} $ D． $ a=\dfrac{{x}_{6}+{x}_{5}+{x}_{4}-{x}_{3}-{x}_{2}-{x}_{1}}{{\left(15T\right) ^ {2}}} $

（3） 甲、乙两组同学各自独立实验，都探究加速度与质量的关系.他们都以小车和砝码的总质量 $ M $ 为横坐标，加速度的倒数 $ \dfrac{1}{a} $ 为纵坐标，甲、乙两组同学分别得到的 $ \dfrac{1}{a}-M $ 图像如图3所示，纵轴上的截距均为 $ b $ .由图像得甲组所用的槽码质量  乙组所用的槽码质量（填“大于”“小于”或“等于”）.根据理论推导可知 $ b= $       .（已知重力加速度为 $ g $ ）

试题资源网 https://stzy.com

图3

答案：

（1） BD

（2） B

（3） 大于； $ \dfrac{1}{g} $

解析：

（1） 为了使小车所受的合外力大小近似等于槽码的总重力,故应使小车质量远大于槽码质量,故 $ \mathrm{A} $ 错误；为了减小误差,拉小车的细绳要平行于长木板,否则小车所受拉力大小等于细绳上的拉力沿木板方向的分力,故 $ \mathrm{B} $ 正确；补偿阻力时需要移去槽码,但不能移去打点计时器和纸带,阻力也包含纸带与限位孔间的阻力,且需要通过纸带上点迹是否均匀来判断小车是否做匀速运动,故 $ \mathrm{C} $ 错误；为了保证小车所受细绳拉力等于小车所受的合力,则需要抬高长木板的右侧以补偿阻力,故 $ \mathrm{D} $ 正确.

（2） 根据逐差法可知 $ {a}_{1}=\dfrac{{x}_{34}-{x}_{01}}{3×(5T)^{2}}=\dfrac{{x}_{4}-{x}_{3}-{x}_{1}}{3×(5T)^{2}} $ , $ {a}_{2}=\dfrac{{x}_{45}-{x}_{12}}{3× (5T)^{2}}=\dfrac{{x}_{5}-{x}_{4}- ({x}_{2}-{x}_{1} )}{3× (5T)^{2}} $ , $ {a}_{3}=\dfrac{{x}_{56}-{x}_{23}}{3× (5T)^{2}}=\dfrac{{x}_{6}-{x}_{5}- ({x}_{3}-{x}_{2} )}{3× (5T)^{2}} $ ,则加速度为 $ a=\dfrac{{a}_{1}+{a}_{2}+{a}_{3}}{3}=\dfrac{{x}_{6}-2{x}_{3}}{{\left(15T\right) ^ {2}}} $ ,故选 $ \mathrm{B} $ .

（3） 设槽码的质量为 $ m $ ,细绳的拉力为 $ F $ ,由牛顿第二定律（下节学习）,对槽码有 $ mg-F=ma $ ,对小车和砝码有 $ F=Ma $ ,整理得 $ \dfrac{1}{a}=\dfrac{1}{mg}\cdot M+\dfrac{1}{g} $ ,故 $ \dfrac{1}{a}-M $ 图线的斜率越小,槽码的质量 $ m $ 越大,由题图3可知甲组所得图线的斜率较小,故甲组所用的槽码质量大于乙组所用的槽码质量.根据理论推导可知,纵轴截距 $ b=\dfrac{1}{g} $ .

3．为了探究物体质量一定时加速度与力的关系，某同学设计了如图甲所示的实验装置.其中遮光条的宽度为 $ d $ ，光电门1、2之间的距离为 $ L $ ，力传感器可测出轻绳中的拉力大小.

试题资源网 https://stzy.com

甲

（1） 在本实验中，一定要进行的操作是    .

A．实验前，要调节气垫导轨，使其水平

B．用秒表测量并记录滑块从光电门2到光电门1所用的时间

C．保证砂和砂桶的总质量 $ m $ 远小于滑块和遮光条的总质量 $ M $

（2） 在实验中得到遮光条经过光电门1、2的挡光时间分别为 $ {t}_{1} $ 、 $ {t}_{2} $ ，则滑块经过光电门1时的速度大小为 $ {v}_{1}= $         ，滑块的加速度大小 $ a= $                             .（均用题目给出的物理量的字母表示）

（3） 以 $ F $ 为横坐标、 $ (\dfrac{1}{{t}_{1}^{2}}-\dfrac{1}{{t}_{2}^{2}}) $ 为纵坐标，画出的 $ (\dfrac{1}{{t}_{1}^{2}}-\dfrac{1}{{t}_{2}^{2}})-F $ 图像是一条直线，如图乙所示.若求得图线的斜率为 $ k $ ，则滑块和遮光条的总质量 $ M= $           （用题目给出的物理量的字母表示）.

试题资源网 https://stzy.com

乙

答案：

（1） A

（2） $ \dfrac{d}{{t}_{1}} $ ； $ \dfrac{{d}^{2}}{2L}(\dfrac{1}{{t}_{1}^{2}}-\dfrac{1}{{t}_{2}^{2}}) $

（3） $ \dfrac{2L}{k{d}^{2}} $

解析：

（1） 用气垫导轨时,要调节水平,以免重力沿导轨平面向下的分力带来误差,故 $ \mathrm{A} $ 正确；结合实验原理和方案,只需测出滑块分别通过光电门1和光电门2处的速度 $ {v}_{1} $ 、 $ {v}_{2} $ ,由 $ {v}_{2}^{2}-{v}_{1}^{2}=2ax $ 即可算出滑块的加速度大小,从而探究加速度与力的关系,所以不需要记录滑块从光电门2到光电门1所用的时间,故 $ \mathrm{B} $ 错误；由于力传感器可以直接测出轻绳的拉力大小,故不需要保证砂和砂桶的总质量 $ m $ 远小于滑块和遮光条的总质量 $ M $ ,故 $ \mathrm{C} $ 错误.

（2） 结合光电门的工作原理可得,滑块通过光电门1、2时的速度大小分别为 $ {v}_{1}=\dfrac{d}{{t}_{1}} $ 、 $ {v}_{2}=\dfrac{d}{{t}_{2}} $ ,由运动学规律可得 $ {v}_{1}^{2}-{v}_{2}^{2}=2aL $ ,解得 $ a=\dfrac{{d}^{2}}{2L}(\dfrac{1}{{t}_{1}^{2}}-\dfrac{1}{{t}_{2}^{2}}) $ .

（3） 由牛顿第二定律得 $ F=Ma $ ,结合（2）中 $ a $ 的表达式有 $ \dfrac{1}{{t}_{1}^{2}}-\dfrac{1}{{t}_{2}^{2}}=\dfrac{2L}{M{d}^{2}}\cdot F $ ,则 $ (\dfrac{1}{{t}_{1}^{2}}-\dfrac{1}{{t}_{2}^{2}})-F $ 图像的斜率为 $ k=\dfrac{2L}{M{d}^{2}} $ ,解得 $ M=\dfrac{2L}{k{d}^{2}} $ .

4．

试题资源网 https://stzy.com

图（a）

试题资源网 https://stzy.com

（1） 甲、乙、丙三个实验小组分别采用如图（a）、 $ (\mathrm{b}) $ 、 $ (\mathrm{c}) $ 所示的实验装置，验证“当质量一定时，物体运动的加速度与它所受的合力成正比”这一物理规律.已知他们使用的小车完全相同，小车的质量为 $ M $ ，重物的质量为 $ m $ .

① 必须平衡小车和长木板之间的摩擦力的实验小组是    .

A．甲、乙、丙B．甲、乙C．甲、丙

② 实验时，必须满足“ $ M $ 远大于 $ m $ ”的实验小组是    .

（2） 小明同学采用图（c）实验装置探究质量一定时加速度与力的关系的实验时，以弹簧测力计的示数 $ F $ 为横坐标，加速度 $ a $ 为纵坐标，画出 $ a-F $ 图像，求得图线的斜率为 $ k $ ，则小车的质量为    .

A． $ \dfrac{1}{2}k $ B． $ \dfrac{1}{k} $ C． $ \dfrac{2}{k} $ D． $ k $

答案：

① A

② 甲

（2） C

解析：

① 甲、乙、丙三个小组的实验中,小车在长木板上运动过程中均受到摩擦力,所以都需要补偿阻力, $ \mathrm{A} $ 正确.

② 由题图可知,乙小组实验和丙小组实验中细线的拉力分别可以由力传感器和弹簧测力计测量出,不需要用重物的重力替代细线的拉力,所以这两个实验不用满足“ $ M $ 远大于 $ m $ ”,而甲小组实验用重物的重力替代细线的拉力,必须满足“ $ M $ 远大于 $ m $ ”.

（2） 对小车,根据牛顿第二定律（下节学习）有 $ 2F=Ma $ ,解得 $ a=\dfrac{2}{M}F $ ,所以 $ k=\dfrac{2}{M} $ ,可得 $ M=\dfrac{2}{k} $ , $ \mathrm{C} $ 正确.