第1节 牛顿第一定律
一、刷基础
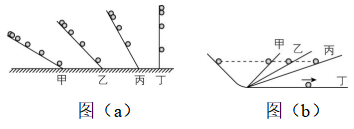
1.伽利略对“自由落体运动”和“运动和力的关系”的研究,开创了科学实验和逻辑推理相结合的重要科学研究方法.图(a)、 $ (\mathrm{b}) $ 分别表示这两项研究中实验和逻辑推理的过程,对这两项研究,下列说法正确的是( )
 (多选)
(多选)
A.图(a)通过对自由落体运动的研究,合理外推得出小球在斜面上做匀变速运动
B.图(a)中先在倾角较小的斜面上进行实验,可“冲淡”重力,使时间测量更容易
C.图(b)中完全没有摩擦阻力的斜面实际是存在的,实验可实际完成
D.图(b)中伽利略通过逻辑推理得出物体的运动不需要力来维持
答案:BD
解析:伽利略设想物体下落的速度与时间成正比,因为当时无法测量物体的瞬时速度,所以伽利略通过数学推导证明,如果速度与时间成正比,那么位移与时间的二次方就成正比.由于当时用滴水法计时,无法记录自由落体的时间,伽利略设计了让铜球沿阻力很小的斜面滚下,来“冲淡”重力的作用效果,而铜球在斜面上运动的加速度要比它竖直下落的加速度小得多,运动相同位移所用时间长得多,所以容易测量.伽利略做了上百次实验,并通过抽象思维在实验结果上进行了合理外推,得出了正确结论,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;完全没有摩擦阻力的斜面是不存在的,故 $ \mathrm{C} $ 错误;伽利略用抽象思维、数学推导和科学实验相结合的方法得到物体的运动不需要力来维持的结论,故 $ \mathrm{D} $ 正确.
2.如图所示,物理老师用一根筷子穿透一个苹果,他一只手拿筷子,另一只手拿锤子敲击筷子上端,发现苹果会沿着筷子向上“爬”,下列说法正确的是( )

A.苹果越小越容易完成该实验
B.苹果受到筷子的向上的力才会向上“爬”
C.该实验主要是利用牛顿第一定律
D.该实验主要是利用牛顿第三定律
答案:C
解析:该实验的原理是牛顿第一定律,即惯性定律,任何物体总要保持原有的运动状态(静止或匀速直线运动),除非作用在它上面的力迫使它改变这种状态.当拿锤子敲击筷子上端时,筷子快速下降,而苹果由于具有惯性,要保持原有的运动状态,位置保持不变,则苹果相对筷子向上运动,即苹果会沿着筷子向上“爬”,不是苹果受到筷子的向上的力,苹果越大,质量越大,惯性越大,越容易完成该实验.故 $ \mathrm{C} $ 正确.
3.关于生活中的一些现象,下列说法正确的是( )(多选)
A.汽车匀速转弯时,汽车的运动状态没有发生变化
B.公交车紧急刹车时,公交车上的乘客会向前倾,是因为乘客具有惯性
C.货运列车在有些车站加挂车厢,这会增大它的惯性
D.“强弩之末,势不能穿鲁缟”,是因为弩箭的惯性减小了
答案:BC
解析:汽车匀速转弯时,汽车的速度方向发生变化,运动状态发生变化,故 $ \mathrm{A} $ 错误;公交车紧急刹车时,公交车上的乘客会向前倾,是因为乘客具有惯性,故 $ \mathrm{B} $ 正确;货运列车在有些车站加挂车厢,这会增大它的质量,从而增大它的惯性,故 $ \mathrm{C} $ 正确;物体的惯性只与质量有关,与其他因素无关,故 $ \mathrm{D} $ 错误.
4.如图所示是快速抽桌布实验,在实验中用“水杯塔”来模拟桌布上物品,挑战者迅速向右将桌布抽出,而“水杯塔”只是在桌面上短暂滑动一下便停了下来.下列说法正确的是( )

A.“水杯塔”中的水越少,则“水杯塔”的惯性越大
B.手拉动桌布时桌布对“水杯塔”的摩擦力的方向向左
C.整个过程中“水杯塔”受到的摩擦力方向发生了改变
D.拉动桌布越快,“水杯塔”受到的摩擦力越大
答案:C
解析:“水杯塔”的惯性与质量有关,水越少,则“水杯塔”的惯性越小,故 $ \mathrm{A} $ 错误;手拉动桌布时,“水杯塔”相对于桌布向左运动,桌布对“水杯塔”的摩擦力的方向向右,故 $ \mathrm{B} $ 错误;“水杯塔”受到桌布的摩擦力向右,桌布被抽出后,“水杯塔”在桌面上相对于桌面向右运动,则桌面对“水杯塔”的摩擦力向左,故 $ \mathrm{C} $ 正确;“水杯塔”受到的滑动摩擦力大小与动摩擦因数和正压力有关,与拉动桌布的快慢无关,故 $ \mathrm{D} $ 错误.
5.下列关于惯性的说法正确的是( )(多选)
A.惯性是物体抵抗运动状态变化的性质
B.当物体受外力作用时,惯性表现为改变物体运动状态的难易程度
C.质量相同的两个物体受到相同阻力时,速度大的不容易停下来,故速度大的物体惯性大
D.惯性是一种力,物体保持原来运动状态是因为受到惯性力的作用
答案:AB
解析:惯性是保持物体原来运动状态的性质,即抵抗运动状态变化的性质,故 $ \mathrm{A} $ 正确;当物体受外力作用时,惯性表现为改变物体运动状态的难易程度,故 $ \mathrm{B} $ 正确;质量相同的两个物体,其惯性相同,故 $ \mathrm{C} $ 错误;惯性不是力,是物体的固有属性,故 $ \mathrm{D} $ 错误.
二、刷提升
1.伽利略根据“对接斜面实验”提出,“任何速度一旦施加给一个运动着的物体,只要除去加速或减速的外因,此速度就可保持不变,不过这是只能在水平面上发生的一种情形.”其实,伽利略的表述中有明确的“原惯性”的缺陷;他还把重力看作物体固有的力,把它排除出了外力之列.下列说法正确的是( )
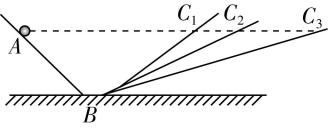
A.“重力与质量都是物体内在的属性”这一说法是正确的
B.伽利略根据如图所示的实验的结论,定义了速度的概念
C.笛卡儿提出运动物体没有外力的作用时,将继续以同一速度沿同一直线运动
D.牛顿根据理想斜面实验,提出力是改变物体运动状态的原因
答案:C
解析:质量是物体内在的属性,但重力不是,故 $ \mathrm{A} $ 错误;伽利略根据题图所示的实验的结论,提出了惯性的概念,故 $ \mathrm{B} $ 错误;笛卡儿提出运动物体没有外力的作用时,将继续以同一速度沿同一直线运动,故 $ \mathrm{C} $ 正确;伽利略根据理想斜面实验,提出力是改变物体运动状态的原因,故 $ \mathrm{D} $ 错误.
2.如图所示,要将卡在球筒中的羽毛球取出,可以有多种方案,方案一:一手拿着球筒的中部,另一手用力击打球筒的上端;方案二:手持球筒,使羽毛球与球筒一起下落敲击水平面,假设球筒与水平面碰后速度立即变为零,则( )
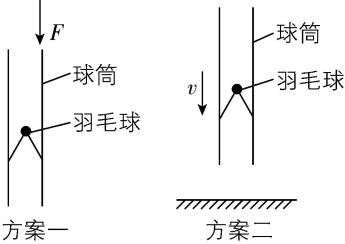
A.方案一利用羽毛球的惯性,使其从球筒上端出来
B.方案一利用球筒的惯性,使羽毛球从球筒下端出来
C.方案二利用羽毛球受到的重力,使其从球筒下端出来
D.方案二中球筒敲击水平面后速度变为零,其惯性随之消失
答案:A
解析:方案一中用力击打球筒的上端,球筒向下运动,利用羽毛球的惯性,使其从球筒上端出来,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;方案二中羽毛球与球筒一起下落敲击水平面,球筒与水平面碰后速度立即变为零,利用羽毛球的惯性,使其从球筒下端出来,故 $ \mathrm{C} $ 错误;惯性是物体本身的属性,与速度无关,故 $ \mathrm{D} $ 错误.
3.如图所示,一个劈形物体 $ A $ (各面均光滑)放在固定的斜面上,上表面水平,在其上表面放一个光滑小球 $ B $ .劈形物体由静止开始释放,则小球在碰到斜面前的运动轨迹是( )
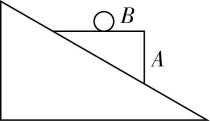
A.沿斜面向下的直线
B.竖直向下的直线
C.无规则的曲线
D.垂直斜面的直线
答案:B
解析:由于小球放在劈形物体 $ A $ 上,劈形物体 $ A $ 的上表面光滑,在劈形物体 $ A $ 下滑过程中,小球在水平方向上不受外力作用,则小球在水平方向上没有位移,仅沿竖直方向运动,故 $ \mathrm{B} $ 正确.
4.如图所示,圆柱形玻璃容器内装满液体静置于水平面上,容器中有 $ a $ 、 $ b $ 、 $ c $ 三个不同材质的物块,物块 $ a $ 、 $ c $ 均对容器壁有压力,物块 $ b $ 悬浮于容器内的液体中,忽略 $ a $ 、 $ c $ 与容器壁间的摩擦.现给容器施加一水平向右的恒力,使容器向右做匀加速直线运动.下列说法正确的是( )
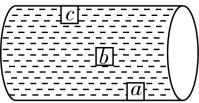
A.三个物块将保持相对位置不变,与容器一起向右做加速运动
B.物块 $ a $ 将相对于容器向右运动,最终与容器右侧壁相互挤压
C.物块 $ b $ 将相对于容器向左运动,最终与容器左侧壁相互挤压
D.物块 $ c $ 将相对于容器向右运动,最终与容器右侧壁相互挤压
答案:D
解析: $ c $ 对容器上壁有压力,可知 $ c $ 排开液体的质量大于本身的质量, $ b $ 悬浮于容器内的液体中,可知 $ b $ 排开液体的质量等于本身的质量, $ a $ 对容器下壁有压力,可知 $ a $ 排开液体的质量小于本身的质量.当容器向右做匀加速运动时,结合牛顿第一定律可知物块 $ a $ 将相对于容器向左运动,最终与容器左侧壁相互挤压,物块 $ b $ (可将 $ b $ 视为液体的一部分)将相对于容器保持静止,与容器一起做匀加速运动,物块 $ c $ (可将 $ c $ 想象为一个小气泡)因相等体积的液体向左运动,物块 $ c $ 将相对于容器向右运动,最终与容器右侧壁相互挤压.故选 $ \mathrm{D} $ .
5.如图所示,在水平地面上,甲、乙两位小朋友踩着滑板面对面静止站立,甲的质量为 $ {m}_{1}=30\mathrm{k}\mathrm{g} $ ,乙的质量为 $ {m}_{2}=25\mathrm{k}\mathrm{g} $ ,他们相互轻推一下对方后,甲向左后退 $ 2.5\mathrm{m} $ 后停下,乙向右后退 $ 3\mathrm{m} $ 后停下,下列判断正确的是( )
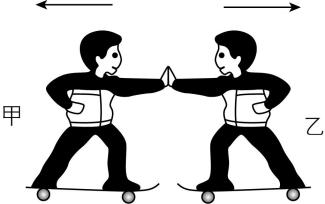
A.甲的惯性更大
B.乙的惯性更大
C.甲、乙的惯性一样大
D.甲、乙的惯性大小与速度有关
答案:A
解析:质量越大的物体其惯性越大,质量是衡量物体惯性大小的唯一量度,即惯性的大小与物体做什么样的运动无关,也跟物体速度的大小无关,只与物体的质量有关,所以甲的惯性更大, $ \mathrm{A} $ 正确.
 (多选)
(多选)





