课时1 力的合成
一、刷基础
1.图1中两人分别用力 $ {F}_{1} $ 、 $ {F}_{2} $ 互成角度地共同提着石块保持静止.图2中吊车单独用力 $ F $ 悬吊着该石块静止.则下列说法正确的是( )
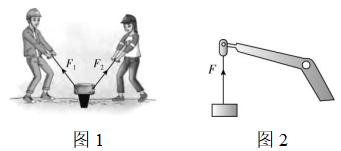 (多选)
(多选)
A. $ {F}_{1} $ 、 $ {F}_{2} $ 为 $ F $ 的合力
B. $ F $ 为 $ {F}_{1} $ 、 $ {F}_{2} $ 的合力
C. $ F $ 的大小可能等于 $ {F}_{1} $ 、 $ {F}_{2} $ 的大小
D. $ F $ 的大小一定等于 $ {F}_{1} $ 、 $ {F}_{2} $ 的大小之和
答案:BC
解析:根据题意可知, $ {F}_{1} $ 、 $ {F}_{2} $ 共同作用的效果与 $ F $ 单独作用的效果相同,根据合力与分力的定义可知 $ F $ 为 $ {F}_{1} $ 、 $ {F}_{2} $ 的合力, $ {F}_{1} $ 、 $ {F}_{2} $ 为 $ F $ 的分力,故 $ \mathrm{A} $ 错误, $ \mathrm{B} $ 正确;若 $ {F}_{1} $ 、 $ {F}_{2} $ 与竖直方向的夹角均为 $ {60}^{\circ } $ ,根据对称性可知, $ {F}_{1} $ 、 $ {F}_{2} $ 两个力的大小相等,由于此时 $ {F}_{1} $ 、 $ {F}_{2} $ 之间的夹角为 $ {120}^{\circ } $ ,根据平行四边形定则可知,合力 $ F $ 的大小等于 $ {F}_{1} $ 、 $ {F}_{2} $ 的大小,即 $ F $ 的大小可能等于 $ {F}_{1} $ 、 $ {F}_{2} $ 的大小,故 $ \mathrm{C} $ 正确;当 $ {F}_{1} $ 、 $ {F}_{2} $ 的方向均竖直向上时,根据力的合成可知,此时 $ F $ 的大小等于 $ {F}_{1} $ 、 $ {F}_{2} $ 的大小之和,当 $ {F}_{1} $ 、 $ {F}_{2} $ 之间存在一定的夹角时,根据平行四边形定则,结合三角形的两边之和大于第三边可知,此时 $ F $ 的大小小于 $ {F}_{1} $ 、 $ {F}_{2} $ 的大小之和,故 $ \mathrm{D} $ 错误.
2.分别表示 $ {F}_{1} $ 、 $ {F}_{2} $ 、 $ {F}_{3} $ 、 $ {F}_{4} $ 、 $ {F}_{5} $ 五个力的有向线段构成的几何图形如图所示,已知 $ {F}_{5}=5\mathrm{N} $ ,方向水平向左.则可以等效替代这五个力的合力的力为( )
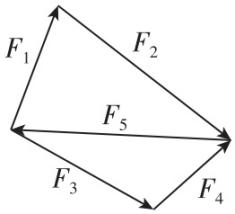
A. $ 5\mathrm{N} $ ,方向水平向左
B. $ 5\mathrm{N} $ ,方向水平向右
C. $ 10\mathrm{N} $ ,方向水平向右
D. $ 15\mathrm{N} $ ,方向水平向左
答案:B
解析:根据矢量合成的法则可知, $ {F}_{1} $ 和 $ {F}_{2} $ 的合力与 $ {F}_{5} $ 等大反向, $ {F}_{3} $ 和 $ {F}_{4} $ 的合力与 $ {F}_{5} $ 等大反向,则这五个力的合力大小等于 $ 5\mathrm{N} $ ,方向水平向右.故选 $ \mathrm{B} $ .
3.如图所示,作用在一个物体上的六个共点力的大小分别为 $ F $ 、 $ 2F $ 、 $ 3F $ 、 $ 4F $ 、 $ 5F $ 、 $ 6F $ ,相邻两力间的夹角均为 $ {60}^{\circ } $ ,则其合力大小为( )
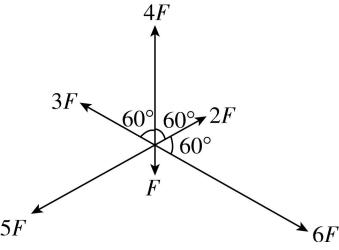
A. $ F $
B. $ 2F $
C. $ 6F $
D.0
答案:D
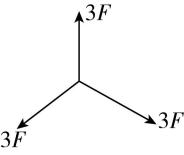
解析: $ 4F $ 与 $ F $ 两力的合力为 $ 3F $ ,沿 $ 4F $ 的方向; $ 3F $ 与 $ 6F $ 两力的合力为 $ 3F $ ,沿 $ 6F $ 的方向; $ 2F $ 与 $ 5F $ 两力的合力为 $ 3F $ ,沿 $ 5F $ 的方向.将同一直线上的力合成后,物体受力如图所示,三力大小相等,夹角互为 $ {120}^{\circ } $ ,则合力为0.故选 $ \mathrm{D} $ .
4.如图所示,有五个力作用于同一点 $ O $ ,表示这五个力的有向线段恰分别构成一个正六边形的两条邻边和内角的连线.已知 $ {F}_{2}=10\mathrm{N} $ ,则这五个力的合力大小为( )
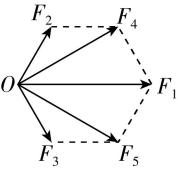
A. $ 20\mathrm{N} $
B. $ 30\mathrm{N} $
C. $ 40\mathrm{N} $
D. $ 60\mathrm{N} $
答案:D
解析:解法一:利用平行四边形定则,如图甲所示.
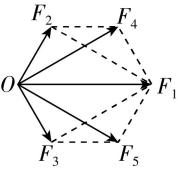
甲
最大力为 $ {F}_{1} $ ,根据平行四边形定则可知, $ {F}_{3} $ 与 $ {F}_{4} $ 的合力与 $ {F}_{1} $ 相等, $ {F}_{2} $ 与 $ {F}_{5} $ 的合力与 $ {F}_{1} $ 相等,这五个力的合力为 $ 3{F}_{1} $ ,已知 $ {F}_{2}=10\mathrm{N} $ ,根据几何关系可知 $ {F}_{1}=20\mathrm{N} $ ,所以合力的大小为 $ F=3{F}_{1}=60\mathrm{N} $ ,故 $ \mathrm{D} $ 正确.
解法二:利用三角形定则,如图乙所示.
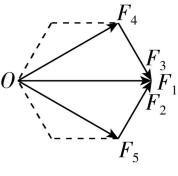
乙
将 $ {F}_{2} $ 、 $ {F}_{3} $ 分别平移到 $ {F}_{5} $ 与 $ {F}_{1} $ 、 $ {F}_{4} $ 与 $ {F}_{1} $ 的末端之间, $ {F}_{3} $ 、 $ {F}_{4} $ 的合力与 $ {F}_{1} $ 相等, $ {F}_{5} $ 、 $ {F}_{2} $ 的合力与 $ {F}_{1} $ 相等,由几何关系可知 $ {F}_{1}=2{F}_{2}=20\mathrm{N} $ ,故这五个力的合力大小为 $ F=3{F}_{1}=60\mathrm{N} $ ,故 $ \mathrm{D} $ 正确.
解法三:利用对称法,如图丙所示.
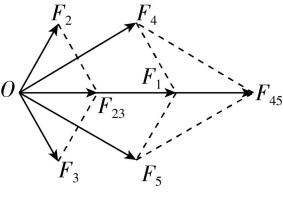
丙
由正六边形特点和对称性可知, $ {F}_{2} $ 和 $ {F}_{3} $ 的夹角为 $ {120}^{\circ } $ , $ {F}_{2}={F}_{3} $ ,则合力在其夹角的角平分线上,合力的大小等于其分力的大小,故 $ {F}_{2} $ 和 $ {F}_{3} $ 的合力大小 $ {F}_{23}={F}_{2}=10\mathrm{N} $ ,同理, $ {F}_{4} $ 和 $ {F}_{5} $ 的合力也在其夹角的角平分线上,由几何关系可知 $ {F}_{1}=2{F}_{2}=20\mathrm{N} $ , $ {F}_{45}=30\mathrm{N} $ ,故这五个力的合力大小为 $ F={F}_{1}+{F}_{23}+{F}_{45}=60\mathrm{N} $ ,故 $ \mathrm{D} $ 正确.
解法四:利用正交分解法,以点 $ O $ 为原点、 $ {F}_{1} $ 所在方向为 $ x $ 轴建立如图丁所示的平面直角坐标系.
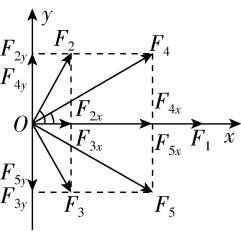
丁
将 $ {F}_{2}\mathrm{~}{F}_{5} $ 正交分解,在 $ y $ 轴方向合力为零,故这五个力的合力等于在 $ x $ 轴方向的合力,有 $ F={F}_{1}+{F}_{2} \cos {60}^{\circ }+{F}_{3} \cos {60}^{\circ }+{F}_{4} \cos {30}^{\circ }+{F}_{5} \cos {30}^{\circ } $ ,已知 $ {F}_{2}=10\mathrm{N} $ ,由几何关系得 $ {F}_{1}=20\mathrm{N} $ , $ {F}_{3}={F}_{2}=10\mathrm{N} $ , $ {F}_{4}={F}_{5}=10\sqrt{3}\mathrm{N} $ ,故这五个力的合力大小为 $ F=60\mathrm{N} $ ,故 $ \mathrm{D} $ 正确.
5.两个力 $ {F}_{1} $ 和 $ {F}_{2} $ 之间的夹角为 $ \theta $ ,其合力为 $ F $ .以下说法正确的是( )
 (多选)
(多选)
A.合力 $ F $ 总比分力 $ {F}_{1} $ 和 $ {F}_{2} $ 中的任何一个力都大
B.若 $ {F}_{1} $ 和 $ {F}_{2} $ 大小不变, $ \theta $ 减小,合力 $ F $ 一定增大
C.若夹角 $ \theta $ 不变, $ {F}_{1} $ 大小不变, $ {F}_{2} $ 增大,合力 $ F $ 可能减小
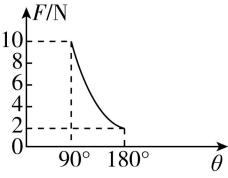
D.若 $ {F}_{1} $ 和 $ {F}_{2} $ 大小不变,合力 $ F $ 与 $ \theta $ 的部分关系图像如图所示,则任意改变 $ \theta $ ,能得到的合力大小的变化范围是 $ 2\mathrm{N}⩽ F⩽ 10\mathrm{N} $
答案:BC
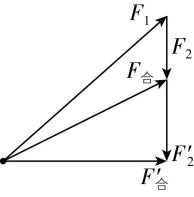
解析:合力 $ F $ 的取值范围是 $ |{F}_{1}-{F}_{2}|⩽ F⩽ {F}_{1}+{F}_{2} $ ,所以合力 $ F $ 不一定总比分力 $ {F}_{1} $ 和 $ {F}_{2} $ 中的任何一个力都大,故 $ \mathrm{A} $ 错误.若 $ {F}_{1} $ 和 $ {F}_{2} $ 大小不变,根据平行四边形定则可知, $ \theta $ 越小,合力 $ F $ 越大,故 $ \mathrm{B} $ 正确.若夹角 $ \theta $ 不变, $ {F}_{1} $ 大小不变, $ {F}_{2} $ 增大,当 $ \theta $ 为钝角时,则可能出现如图所示的情况, $ F{\prime }_{合} < {F}_{合} $ ,故 $ \mathrm{C} $ 正确.由题图可得,当 $ \theta ={180}^{\circ } $ 时,合力最小为 $ 2\mathrm{N} $ ,即 $ |{F}_{1}-{F}_{2}|=2\mathrm{N} $ ,当 $ \theta ={90}^{\circ } $ 时,合力为 $ 10\mathrm{N} $ ,即 $ \sqrt{{F}_{1}^{2}+{F}_{2}^{2}}=10\mathrm{N} $ ,解得 $ {F}_{1}=6\mathrm{N} $ , $ {F}_{2}=8\mathrm{N} $ 或 $ {F}_{1}=8\mathrm{N} $ , $ {F}_{2}=6\mathrm{N} $ ,故 $ 2\mathrm{N}⩽ F⩽ 14\mathrm{N} $ ,故 $ \mathrm{D} $ 错误.
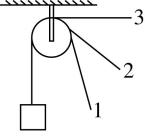
6.如图所示,一个物体由绕过轻质定滑轮的轻质细绳拉着,分别被图中所示的三种情况拉住静止不动,在这三种情况下,若绳的拉力大小分别为 $ {T}_{1} $ 、 $ {T}_{2} $ 、 $ {T}_{3} $ ,轴心对定滑轮的支持力大小分别为 $ {N}_{1} $ 、 $ {N}_{2} $ 、 $ {N}_{3} $ ,若不计滑轮的质量及摩擦,则( )
A. $ {T}_{1}={T}_{2}={T}_{3} $ , $ {N}_{1}={N}_{2}={N}_{3} $
B. $ {T}_{1} > {T}_{2} > {T}_{3} $ , $ {N}_{1}={N}_{2}={N}_{3} $
C. $ {T}_{1}={T}_{2}={T}_{3} $ , $ {N}_{1} > {N}_{2} > {N}_{3} $
D. $ {T}_{1} < {T}_{2} < {T}_{3} $ , $ {N}_{1} < {N}_{2} < {N}_{3} $
答案:C
解析:设物体的重力为 $ G $ ,由于定滑轮只改变力的方向,不改变力的大小,所以拉力的大小关系为 $ {T}_{1}={T}_{2}={T}_{3}=G $ ,由于轴心对定滑轮的支持力大小等于细绳对定滑轮的合力大小,而已知两个分力的大小相等,其合力与两分力的夹角 $ \theta $ 满足关系式 $ F=2G \cos \dfrac{\theta }{2} $ ,可知 $ \theta $ 越大, $ F $ 越小,故 $ {N}_{1} > {N}_{2} > {N}_{3} $ ,选项 $ \mathrm{C} $ 正确.
二、刷提升
1.三个共点力大小分别是 $ {F}_{1} $ 、 $ {F}_{2} $ 、 $ {F}_{3} $ ,它们的合力的大小为 $ F $ ,则( )(多选)
A. $ F $ 的取值范围一定是 $ 0⩽ F⩽ {F}_{1}+{F}_{2}+{F}_{3} $
B. $ F $ 可能与 $ {F}_{1} $ 、 $ {F}_{2} $ 、 $ {F}_{3} $ 中的某一个力相等
C.若 $ {F}_{1}:{F}_{2}:{F}_{3}=3:6:8 $ ,只要适当调整它们之间的夹角,一定能使合力为零
D.若 $ {F}_{1}:{F}_{2}:{F}_{3}=3:6:2 $ ,只要适当调整它们之间的夹角,一定能使合力为零
答案:BC
解析:三个共点力的合力最大值为三个力的代数和,合力最小值不一定是零,只有当其中一个力的大小在另外两个力的合力范围内,三个力的最小合力才会为零, $ \mathrm{A} $ 错误;由平行四边形定则可知, $ F $ 可能与 $ {F}_{1} $ 、 $ {F}_{2} $ 、 $ {F}_{3} $ 中的某一个力相等, $ \mathrm{B} $ 正确;设 $ {F}_{1}=3\mathrm{N} $ , $ {F}_{2}=6\mathrm{N} $ , $ {F}_{3}=8\mathrm{N} $ , $ {F}_{2} $ 与 $ {F}_{3} $ 的合力介于 $ 2\mathrm{N} $ 到 $ 14\mathrm{N} $ 之间, $ {F}_{1} $ 的大小处于该范围之间,只要适当调整它们之间的夹角,就能使 $ {F}_{2} $ 、 $ {F}_{3} $ 的合力与 $ {F}_{1} $ 等大、反向,三力的合力就为零,同理可知,若 $ {F}_{1}:{F}_{2}:{F}_{3}=3:6:2 $ ,三力的合力不可能为零, $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
2.两个大小相等的共点力 $ {F}_{1} $ 、 $ {F}_{2} $ ,当它们间的夹角为 $ {90}^{\circ } $ 时,合力大小为 $ 10\mathrm{N} $ .那么当 $ {F}_{1} $ 不变, $ {F}_{2} $ 旋转 $ {30}^{\circ } $ 时,合力的大小可能为( )(多选)
A. $ 5\mathrm{N} $
B. $ 5\sqrt{2}\mathrm{N} $
C. $ 5\sqrt{3}\mathrm{N} $
D. $ 5\sqrt{6}\mathrm{N} $
答案:BD
解析:设两个相等的共点力大小为 $ {F}_{1}={F}_{2}=F $ ,由题意知当它们间的夹角为 $ {90}^{\circ } $ 时,合力大小为 $ 10\mathrm{N} $ ,由勾股定理得 $ 10\mathrm{N}=\sqrt{2{F}^{2}} $ ,解得 $ F=5\sqrt{2}\mathrm{N} $ ,那么当 $ {F}_{1} $ 不变, $ {F}_{2} $ 旋转 $ {30}^{\circ } $ 时,二力夹角为 $ {120}^{\circ } $ 或 $ {60}^{\circ } $ ,结合平行四边形定则,由几何关系可知二者的合力大小为 $ {F}_{合1}=2F \cos \dfrac{{120}^{\circ }}{2}=5\sqrt{2}\mathrm{N} $ ,或 $ {F}_{合2}=2F \cos \dfrac{{60}^{\circ }}{2}=5\sqrt{6}\mathrm{N} $ ,故选 $ \mathrm{B} $ 、 $ \mathrm{D} $ .
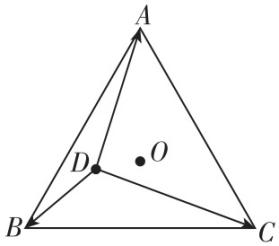
3.如图所示, $ O $ 是等边三角形 $ ABC $ 的中心, $ D $ 是三角形中的任意点,如果作矢量 $ \stackrel{\to }{DA} $ 、 $ \stackrel{\to }{DB} $ 、 $ \stackrel{\to }{DC} $ 分别表示三个力,三个力的方向如图中箭头所示,则这三个力的合力大小用 $ DO $ 的长度表示为( )
A. $ DO $
B. $ 2DO $
C. $ 3DO $
D. $ 4DO $
答案:C
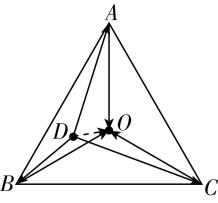
解析:因为 $ O $ 是等边三角形 $ ABC $ 的中心,现增加三个力,分别用矢量 $ \stackrel{\to }{AO} $ 、 $ \stackrel{\to }{BO} $ 、 $ \stackrel{\to }{CO} $ 表示,如图所示,因为矢量 $ \stackrel{\to }{AO} $ 、 $ \stackrel{\to }{BO} $ 、 $ \stackrel{\to }{CO} $ 互成 $ {120}^{\circ } $ 夹角,故 $ \stackrel{\to }{AO} $ 、 $ \stackrel{\to }{BO} $ 、 $ \stackrel{\to }{CO} $ 三者的合力为零,不影响 $ \stackrel{\to }{DA} $ 、 $ \stackrel{\to }{DB} $ 、 $ \stackrel{\to }{DC} $ 三力的合成,根据三角形定则可知, $ \stackrel{\to }{DA} $ 与 $ \stackrel{\to }{AO} $ 的合力为 $ \stackrel{\to }{DO} $ , $ \stackrel{\to }{DB} $ 与 $ \stackrel{\to }{BO} $ 的合力为 $ \stackrel{\to }{DO} $ , $ \stackrel{\to }{DC} $ 与 $ \stackrel{\to }{CO} $ 的合力为 $ \stackrel{\to }{DO} $ ,故 $ \stackrel{\to }{DA} $ 、 $ \stackrel{\to }{DB} $ 、 $ \stackrel{\to }{DC} $ 三个力的合力大小用 $ DO $ 长度可表示为 $ 3DO $ , $ \mathrm{C} $ 正确.
4.两个共点力 $ {F}_{1} $ 、 $ {F}_{2} $ 大小不同,不共线,它们的合力为 $ F $ ,则( )(多选)
A. $ {F}_{1} $ 、 $ {F}_{2} $ 同时增大一倍, $ F $ 一定增大一倍
B. $ {F}_{1} $ 、 $ {F}_{2} $ 同时增大 $ 10\mathrm{N} $ , $ F $ 也增大 $ 10\mathrm{N} $
C. $ {F}_{1} $ 增大 $ 10\mathrm{N} $ , $ {F}_{2} $ 减小 $ 10\mathrm{N} $ , $ F $ 一定不变
D.若 $ {F}_{1} $ 、 $ {F}_{2} $ 中的一个增大, $ F $ 可能减小
答案:AD
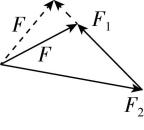
解析: $ {F}_{1} $ 、 $ {F}_{2} $ 同时增大一倍,即都变为原来的2倍,根据平行四边形定则可知,合力将变为原来的2倍,即 $ F $ 一定增大一倍,故 $ \mathrm{A} $ 正确;根据平行四边形定则, $ {F}_{1} $ 、 $ {F}_{2} $ 都增大 $ 10\mathrm{N} $ ,若方向相同, $ F $ 增大 $ 20\mathrm{N} $ ,若方向相反, $ F $ 不变,若 $ {F}_{1} $ 、 $ {F}_{2} $ 不共线,则 $ F $ 的增加量应该在 $ 0\sim 20\mathrm{N} $ 之间,不一定增大 $ 10\mathrm{N} $ ,故 $ \mathrm{B} $ 错误; $ {F}_{1} $ 增大 $ 10\mathrm{N} $ , $ {F}_{2} $ 减小 $ 10\mathrm{N} $ ,当 $ {F}_{1} $ 、 $ {F}_{2} $ 不共线时, $ F $ 的方向一定变化,故 $ \mathrm{C} $ 错误;如图所示,若 $ {F}_{1} $ 、 $ {F}_{2} $ 中的一个增大(图中的 $ {F}_{1} $ 增大),根据平行四边形定则可知,合力 $ F $ 可能减小,故 $ \mathrm{D} $ 正确.
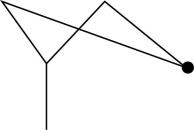
5.如图所示,一个“ $ \mathrm{Y} $ ”字形弹弓顶部两端系着两根相同的橡皮条,橡皮条的原长均为 $ L $ ,橡皮条的末端连接裹片(长度不计),将弹丸放在裹片中,每根橡皮条均被拉伸至长度为 $ 2L $ ,释放裹片,可将弹丸弹出,若此时两橡皮条间的夹角为 $ {60}^{\circ } $ ,释放瞬间弹丸受到的弹力大小为 $ F $ ,已知橡皮条的弹力满足胡克定律且橡皮条始终处于弹性限度内,则橡皮条的劲度系数为( )
A. $ \dfrac{F}{L} $
B. $ \dfrac{\sqrt{3}F}{L} $
C. $ \dfrac{\sqrt{3}F}{2L} $
D. $ \dfrac{\sqrt{3}F}{3L} $
答案:D
解析:每根橡皮条被拉伸至长度为 $ 2L $ 时,根据胡克定律可知,每根橡皮条的弹力大小为 $ {F}_{弹}=k(2L-L)=kL $ ,根据几何关系得 $ F=2{F}_{弹} \cos \dfrac{{60}^{\circ }}{2}=\sqrt{3}{F}_{弹} $ ,联立解得劲度系数 $ k=\dfrac{\sqrt{3}F}{3L} $ ,故 $ \mathrm{D} $ 正确.
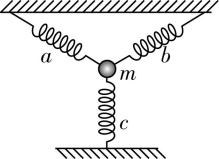
6.如图所示,竖直平面内质量为 $ m $ 的小球与三条相同的轻质弹簧相连接.静止时相邻两弹簧间的夹角均为 $ {120}^{\circ } $ ,已知弹簧 $ c $ 竖直,弹簧 $ a $ 、 $ b $ 对小球的作用力大小均为 $ F $ ,且 $ F=mg $ ,重力加速度为 $ g $ ,则弹簧 $ c $ 对此小球的作用力的大小可能为( )
 (多选)
(多选)
A.0
B. $ mg $
C. $ 2mg $
D. $ 3mg $
答案:AC
解析:当弹簧 $ a $ 、 $ b $ 处于伸长状态时,产生的弹力沿弹簧向上,大小相等,夹角为 $ {120}^{\circ } $ ,由力的合成的特点可知,合力方向竖直向上,大小与两个弹力大小相等,则有 $ {F}_{合}=F=mg $ ,则小球与弹簧 $ c $ 没有相互作用力.当弹簧 $ a $ 、 $ b $ 处于压缩状态时,产生的弹力沿弹簧向下,大小相等,夹角为 $ {120}^{\circ } $ ,由力的合成的特点可知,合力方向竖直向下,大小与两个弹力相等,则有 $ F{\prime }_{合}=F=mg $ ,易知小球与弹簧 $ c $ 的作用力满足 $ {F}_{c}=F{\prime }_{合}+mg=2mg $ , $ \mathrm{A} $ 、 $ \mathrm{C} $ 正确.
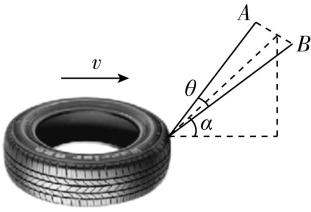
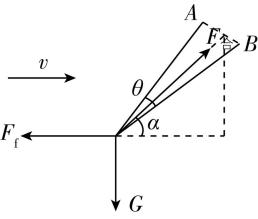
7.如图所示,解放军战士在水平地面上拉着轮胎做匀速直线运动进行负荷训练,运动过程中保持双肩及两绳的端点 $ A $ 、 $ B $ 等高.两绳间的夹角为 $ \theta ={60}^{\circ } $ ,所构成的平面与水平面间的夹角恒为 $ \alpha ={53}^{\circ } $ ,轮胎重力大小为 $ G $ ,地面对轮胎的摩擦阻力大小恒为 $ {F}_{\mathrm{f}} $ ,则每根绳的拉力大小为 $ ( \cos {53}^{\circ }=0.6) $ ( )

A. $ \dfrac{2\sqrt{3}}{9}{F}_{\mathrm{f}} $
B. $ \dfrac{\sqrt{3}}{2}{F}_{\mathrm{f}} $
C. $ \dfrac{5\sqrt{3}}{9}{F}_{\mathrm{f}} $
D. $ \dfrac{2\sqrt{3}}{3}{F}_{\mathrm{f}} $
答案:C
解析:设每根绳的拉力大小为 $ F $ ,则这两根绳拉力的合力 $ {F}_{合}=2F \cos \dfrac{\theta }{2} $ ,方向沿两绳夹角的角平分线,与水平面的夹角为 $ \alpha $ ,受力分析如图所示,对轮胎,由平衡条件有 $ {F}_{合} \cos \alpha ={F}_{\mathrm{f}} $ ,解得 $ F=\dfrac{5\sqrt{3}}{9}{F}_{\mathrm{f}} $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 、 $ \mathrm{D} $ 错误, $ \mathrm{C} $ 正确.
 (多选)
(多选)







 (多选)
(多选)





 (多选)
(多选)

