专题2 运动图像
一、刷题型
1. $ a $ 、 $ b $ 两质点从 $ t=0 $ 时刻开始沿 $ x $ 轴运动,从开始运动到停止运动,它们的位置 $ x $ 随时间 $ t $ 变化的图像分别如图中图线 $ a $ 、 $ b $ 所示,下列说法正确的是( )
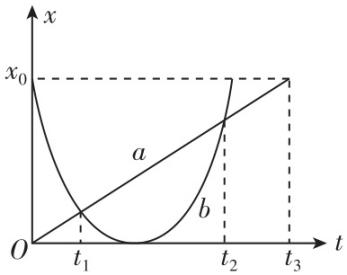
A. $ {t}_{1} $ 时刻 $ a $ 、 $ b $ 运动方向相同
B. $ {t}_{2} $ 时刻 $ a $ 的速度大于 $ b $ 的速度
C. $ {t}_{1}\sim {t}_{2} $ 时间内 $ a $ 的平均速度等于 $ b $ 的平均速度
D. $ 0\sim {t}_{3} $ 时间内 $ a $ 通过的路程等于 $ b $ 通过的路程
答案:C
解析:根据 $ x-t $ 图像的切线斜率表示速度,可知 $ {t}_{1} $ 时刻 $ a $ 沿正方向运动, $ b $ 沿负方向运动, $ {t}_{2} $ 时刻 $ a $ 的速度小于 $ b $ 的速度, $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;由 $ x-t $ 图像可知, $ {t}_{1}\sim {t}_{2} $ 时间内 $ a $ 的位移等于 $ b $ 的位移,则 $ {t}_{1}\sim {t}_{2} $ 时间内 $ a $ 的平均速度等于 $ b $ 的平均速度, $ \mathrm{C} $ 正确;由 $ x-t $ 图像可知, $ 0\sim {t}_{3} $ 时间内 $ a $ 通过的路程为 $ {x}_{0} $ , $ b $ 通过的路程为 $ 2{x}_{0} $ , $ \mathrm{D} $ 错误.
2.甲、乙两个物体沿同一直线运动,甲做匀速运动,乙做初速度为零的匀加速运动,它们的位置 $ x $ 随时间 $ t $ 的变化如图所示,当 $ {t}_{1}=2\mathrm{s} $ 时,甲、乙相距最远, $ AB $ 是乙的图线与 $ t $ 轴交点的切线.则( )
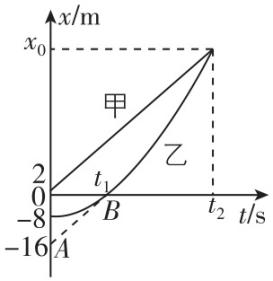
A.甲、乙间的最远距离是 $ 20\mathrm{m} $
B.乙的加速度大小是 $ 2\mathrm{m}/{\mathrm{s}}^{2} $
C.在 $ {t}_{2}=5\mathrm{s} $ 时,甲、乙相遇
D. $ {x}_{0}=40\mathrm{m} $
答案:C
解析:由图像可知在 $ 0\sim 2\mathrm{s} $ 内,乙通过的位移为 $ {x}_{乙}=0\mathrm{m}-(-8\mathrm{m})=8\mathrm{m} $ ,由题意知乙做匀加速直线运动,根据公式 $ {x}_{乙}=\dfrac{1}{2}a{t}_{1}^{2} $ 可得乙的加速度 $ a=4\mathrm{m}/{\mathrm{s}}^{2} $ ,则 $ {t}_{1}=2\mathrm{s} $ 时乙的速度 $ {v}_{乙}=a{t}_{1}=4×2\mathrm{m}/\mathrm{s}=8\mathrm{m}/\mathrm{s} $ ,甲、乙同向运动,当两者的速度相等时相距最远,则 $ {t}_{1}=2\mathrm{s} $ 时甲的速度等于乙的速度,为 $ 8\mathrm{m}/\mathrm{s} $ ,由题意知甲做匀速运动,在 $ 0\sim 2\mathrm{s} $ 内,甲通过的位移为 $ {x}_{甲}={v}_{甲}{t}_{1}=8×2\mathrm{m}=16\mathrm{m} $ ,则甲、乙间的最远距离是 $ x\prime ={x}_{甲}+2\mathrm{m}=16\mathrm{m}+2\mathrm{m}=18\mathrm{m} $ ,故 $ \mathrm{A} $ 、 $ \mathrm{B} $ 错误;在 $ {t}_{2} $ 时,甲、乙相遇,由图像可知 $ t=0 $ 时刻,甲位于 $ x=2\mathrm{m} $ 处,则对甲有 $ {x}_{0}-2\mathrm{m}={v}_{甲}{t}_{2} $ ,对乙有 $ {x}_{0}-(-8\mathrm{m})=\dfrac{1}{2}a{t}_{2}^{2} $ ,联立解得 $ {t}_{2}=5\mathrm{s} $ (另一种解舍去), $ {x}_{0}=42\mathrm{m} $ ,故 $ \mathrm{C} $ 正确, $ \mathrm{D} $ 错误.
3. $ \mathrm{E}\mathrm{T}\mathrm{C} $ 是高速公路上不停车电子收费系统的简称.汽车在进入 $ \mathrm{E}\mathrm{T}\mathrm{C} $ 通道感应识别区前需要减速至 $ 5\mathrm{m}/\mathrm{s} $ ,然后匀速通过感应识别区.甲、乙两辆以 $ 15\mathrm{m}/\mathrm{s} $ 的速度行驶的汽车在进入 $ \mathrm{E}\mathrm{T}\mathrm{C} $ 通道感应识别区前都恰好减速至 $ 5\mathrm{m}/\mathrm{s} $ ,减速过程的 $ v-t $ 图像如图所示,则( )
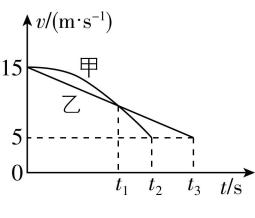
A. $ 0\sim {t}_{1} $ 时间内,甲车的位移等于乙车的位移
B. $ {t}_{1} $ 时刻甲车的加速度等于乙车的加速度
C. $ 0\sim {t}_{1} $ 时间内,甲车的平均速度小于乙车的平均速度
D. $ {t}_{1} $ 时刻甲车距感应识别区的距离小于乙车距感应识别区的距离
答案:D
解析: $ v-t $ 图像与 $ t $ 轴围成的图形面积表示位移,由题图可知, $ 0\sim {t}_{1} $ 时间内,甲车的位移大于乙车的位移,根据 $ \overline{v}=\dfrac{x}{t} $ ,由于时间相同,所以甲车的平均速度大于乙车的平均速度, $ \mathrm{A} $ 、 $ \mathrm{C} $ 错误; $ v-t $ 图像切线的斜率表示加速度,由题图可知, $ {t}_{1} $ 时刻甲车的加速度大于乙车的加速度, $ \mathrm{B} $ 错误;汽车在进入 $ \mathrm{E}\mathrm{T}\mathrm{C} $ 通道感应识别区前都恰好减速至 $ 5\mathrm{m}/\mathrm{s} $ ,从图像上可以看出从 $ {t}_{1} $ 时刻到速度减到 $ 5\mathrm{m}/\mathrm{s} $ 甲的位移小于乙的位移,表明 $ {t}_{1} $ 时刻甲车距感应识别区的距离小于乙车距感应识别区的距离,故 $ \mathrm{D} $ 正确.
4.如图所示为一物体运动的速度—时间图像,图中虚线把图像与两坐标轴所围图形面积等分为7份,总运动时间为 $ {t}_{0} $ ,以下说法正确的是( )
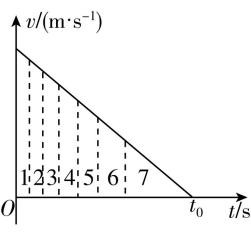
A.物体运动中经过前 $ \dfrac{1}{7} $ 位移所用时间为 $ \dfrac{\sqrt{6}}{\sqrt{7}}{t}_{0} $
B.物体运动中经过前 $ \dfrac{2}{7} $ 位移所用时间为 $ \dfrac{\sqrt{6}}{\sqrt{7}}{t}_{0} $
C.物体运动中经过前 $ \dfrac{3}{7} $ 位移所用时间为 $ \dfrac{2}{\sqrt{7}}{t}_{0} $
D.物体运动中经过第3段位移所用时间为 $ \dfrac{\sqrt{5}-2}{\sqrt{7}}{t}_{0} $
答案:D
解析:用逆向思维法,把物体的运动看成初速度为零的匀加速直线运动,设每份面积表示的位移为 $ s $ ,则 $ \dfrac{1}{2}a{t}_{0}^{2}=7s $ ,逆向经过后6段位移有 $ \dfrac{1}{2}a{t}_{6}^{2}=6s $ ,则物体运动中经过前 $ \dfrac{1}{7} $ 位移的时间为 $ {t}_{0}-{t}_{6}=\dfrac{\sqrt{7}-\sqrt{6}}{\sqrt{7}}{t}_{0} $ ,故 $ \mathrm{A} $ 错误;同理,逆向经过后5段位移有 $ \dfrac{1}{2}a{t}_{5}^{2}=5s $ ,则物体经过前 $ \dfrac{2}{7} $ 位移的时间为 $ {t}_{0}-{t}_{5}=\dfrac{\sqrt{7}-\sqrt{5}}{\sqrt{7}}{t}_{0} $ ,故 $ \mathrm{B} $ 错误;同理,物体经过前 $ \dfrac{3}{7} $ 位移的时间为 $ \dfrac{\sqrt{7}-2}{\sqrt{7}}{t}_{0} $ ,经过第3段位移所用时间为 $ \dfrac{\sqrt{5}-2}{\sqrt{7}}{t}_{0} $ ,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
5.物体沿水平直线运动,某时刻的速度大小为 $ 3\mathrm{m}/\mathrm{s} $ ,方向向右,以此时刻为计时起点,以向右为正方向,该物体加速度随时间变化的 $ a-t $ 图像如图所示,下列说法正确的是( )
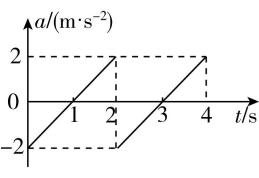
A. $ 0\sim 2\mathrm{s} $ 内,物体的加速度不变
B. $ t=3\mathrm{s} $ 时,物体的速度大小为 $ 2\mathrm{m}/\mathrm{s} $ ,方向向右
C. $ 0\sim 2\mathrm{s} $ 内,物体的位移大小为 $ 5\mathrm{m} $
D.该物体的运动方向时而向左,时而向右
答案:B
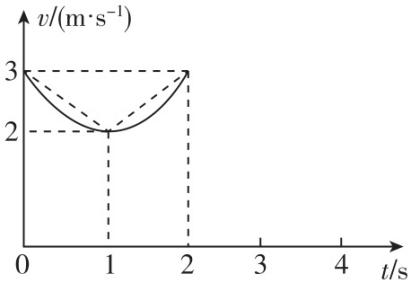
解析:由图像可知,物体的加速度随时间不断变化,故 $ \mathrm{A} $ 错误; $ a-t $ 图像与横轴围成图形的面积表示速度的变化量, $ 0\sim 3\mathrm{s} $ 内,物体的速度变化量为 $ -1\mathrm{m}/\mathrm{s} $ ,所以 $ t=3\mathrm{s} $ 时,物体的速度大小为 $ 2\mathrm{m}/\mathrm{s} $ ,方向向右,故 $ \mathrm{B} $ 正确; $ 0\sim 2\mathrm{s} $ 内物体的 $ v-t $ 图像如图所示,若物体的加速度大小不变,则 $ 0\sim 2\mathrm{s} $ 内物体的位移大小为 $ x\prime =\dfrac{1}{2}×2×1×(2+3)\mathrm{m}=5\mathrm{m} $ ,但物体的加速度先逐渐减小,后逐渐增大,可知物体的位移大小小于 $ 5\mathrm{m} $ , $ \mathrm{C} $ 错误;当 $ t=1\mathrm{s} $ 或 $ 3\mathrm{s} $ 时,速度最小为 $ 2\mathrm{m}/\mathrm{s} $ ,运动过程中物体速度始终为正,所以物体运动方向始终向右, $ \mathrm{D} $ 错误.
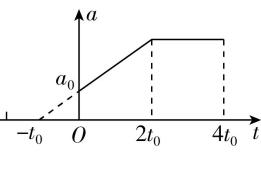
6.小物体 $ P $ 在光滑水平面上正在以速度 $ {v}_{0} $ 匀速运动.从 $ t=0 $ 时刻开始计时, $ P $ 的加速度随时间的变化关系如图所示,以初速度 $ {v}_{0} $ 的方向为正方向,图中 $ {a}_{0} $ 、 $ {t}_{0} $ 为已知量,则小物体 $ P $ ( )
 (多选)
(多选)
A.在 $ 2{t}_{0} $ 和 $ 4{t}_{0} $ 时刻的速度相等
B.在 $ 3{t}_{0} $ 时刻的速度为 $ 7{a}_{0}{t}_{0} $
C.在 $ 2{t}_{0}\sim 4{t}_{0} $ 时间内运动位移为 $ 2{v}_{0}{t}_{0}+14{a}_{0}{t}_{0}^{2} $
D.在 $ {t}_{0} $ 时刻的速度为 $ {v}_{0}+\dfrac{3}{2}{a}_{0}{t}_{0} $
答案:CD
解析:在 $ 2{t}_{0}\sim 4{t}_{0} $ 时间内,物体加速度不变,做匀加速运动,则在 $ 2{t}_{0} $ 和 $ 4{t}_{0} $ 时刻的速度一定不相等, $ \mathrm{A} $ 错误; $ a-t $ 图像中图线与横轴围成图形的面积等于速度的变化量,由函数关系可知 $ t=2{t}_{0} $ 时 $ a=3{a}_{0} $ ,则在 $ 0\sim 3{t}_{0} $ 时间内速度的变化量为 $ \dfrac{1}{2}({a}_{0}+3{a}_{0})\cdot 2{t}_{0}+3{a}_{0}{t}_{0}=7{a}_{0}{t}_{0} $ ,则小物体 $ P $ 在 $ 3{t}_{0} $ 时刻的速度为 $ {v}_{0}+7{a}_{0}{t}_{0} $ , $ \mathrm{B} $ 错误;小物体 $ P $ 在 $ 2{t}_{0} $ 时刻的速度为 $ {v}_{0}+\dfrac{1}{2}({a}_{0}+3{a}_{0})\cdot 2{t}_{0}={v}_{0}+4{a}_{0}{t}_{0} $ ,在 $ 4{t}_{0} $ 时刻的速度为 $ {v}_{0}+\dfrac{1}{2}({a}_{0}+3{a}_{0})\cdot 2{t}_{0}+3{a}_{0}\cdot 2{t}_{0}={v}_{0}+10{a}_{0}{t}_{0} $ ,在 $ 2{t}_{0}\sim 4{t}_{0} $ 时间内,物体做匀加速直线运动,则在 $ 2{t}_{0}\sim 4{t}_{0} $ 时间内的位移为 $ x=\dfrac{{v}_{4t0}^{2}-{v}_{2t0}^{2}}{2×3{a}_{0}}=2{v}_{0}{t}_{0}+14{a}_{0}{t}_{0}^{2} $ , $ \mathrm{C} $ 正确;在 $ {t}_{0} $ 时刻的速度为 $ {v}_{t0}={v}_{0}+\dfrac{{a}_{0}+2{a}_{0}}{2}\cdot {t}_{0}={v}_{0}+\dfrac{3{a}_{0}{t}_{0}}{2} $ , $ \mathrm{D} $ 正确.
7.如图所示,小明绘制了某列车的一段直线运动过程,但未知是出站加速,还是进站刹车,通过图像可知,下列说法错误的是( )
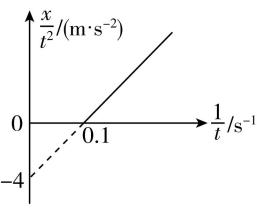
A.小明绘制的是列车进站刹车过程
B.列车的初速度为 $ 40\mathrm{m}/\mathrm{s} $
C.列车的加速度为 $ -4\mathrm{m}/{\mathrm{s}}^{2} $
D.列车前 $ 6\mathrm{s} $ 内的位移为 $ 100\mathrm{m} $
答案:C
解析:由 $ x={v}_{0}t+\dfrac{1}{2}a{t}^{2} $ 得 $ \dfrac{x}{{t}^{2}}={v}_{0}\cdot \dfrac{1}{t}+\dfrac{a}{2} $ ,根据图像可知斜率和纵截距分别为 $ k={v}_{0}=40\mathrm{m}/\mathrm{s} $ , $ b=\dfrac{a}{2}=-4\mathrm{m}/{\mathrm{s}}^{2} $ ,可知列车的初速度和加速度分别为 $ {v}_{0}=40\mathrm{m}/\mathrm{s} $ , $ a=-8\mathrm{m}/{\mathrm{s}}^{2} $ ,可知绘制的是列车进站刹车过程, $ \mathrm{A} $ 、 $ \mathrm{B} $ 正确, $ \mathrm{C} $ 错误;列车停下来所用时间 $ {t}_{0}=\dfrac{0-{v}_{0}}{a}=5\mathrm{s} $ ,则列车前 $ 6\mathrm{s} $ 内的位移 $ x=\dfrac{{v}_{0}}{2}{t}_{0}=100\mathrm{m} $ , $ \mathrm{D} $ 正确.本题选说法错误的,故选 $ \mathrm{C} $ .
8.某质点做直线运动,运动速率的倒数 $ \dfrac{1}{v} $ 与位移 $ x $ 的关系如图所示,下列关于质点运动的说法正确的是( )
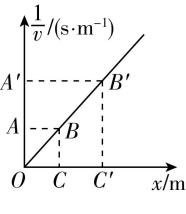
A.质点做匀加速直线运动
B. $ \dfrac{1}{v}-x $ 图线的斜率等于质点运动的加速度
C.四边形 $ AA\prime B\prime B $ 的面积可表示质点从 $ O $ 运动到 $ C\prime $ 所用的时间
D.四边形 $ BB\prime C\prime C $ 的面积可表示质点从 $ C $ 运动到 $ C\prime $ 所用的时间
答案:D
解析: $ \dfrac{1}{v}-x $ 图线为直线,设 $ \dfrac{1}{v}=kx $ ,则 $ vx=\dfrac{1}{k} $ , $ v $ 与 $ x $ 的乘积为常量,随着位移 $ x $ 增大,速率 $ v $ 减小,质点做减速直线运动,故 $ \mathrm{A} $ 错误; $ \dfrac{1}{v}-x $ 图线的斜率为 $ k=\dfrac{1}{vx} $ ,不等于质点运动的加速度,故 $ \mathrm{B} $ 错误;由于三角形 $ OBC $ 的面积为 $ {S}_{1}=\dfrac{1}{2}OC\cdot BC=\dfrac{{x}_{1}}{2{v}_{1}} $ ,可知 $ {S}_{1} $ 可表示从 $ O $ 运动到 $ C $ 所用的时间,同理,从 $ O $ 运动到 $ C\prime $ 所用的时间可表示为 $ {S}_{2}=\dfrac{1}{2}OC\prime \cdot C\prime B\prime =\dfrac{{x}_{2}}{2{v}_{2}} $ ,所以四边形 $ BB\prime C\prime C $ 的面积可表示质点从 $ C $ 运动到 $ C\prime $ 所用的时间,故 $ \mathrm{C} $ 错误, $ \mathrm{D} $ 正确.
9.刹车时间是评价汽车性能的重要参数之一.汽车从时速100公里减速至静止所需的时间通常在 $ 4\sim 5\mathrm{s} $ ,不少博主通过网络直播测试新能源汽车性能,近似认为汽车在刹车时做匀减速直线运动,以初速度方向为正.汽车在刹车后开始计时,该段时间内的运动图像可能正确的是( )(多选)
A.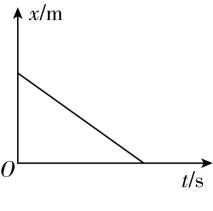
B.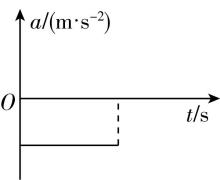
C.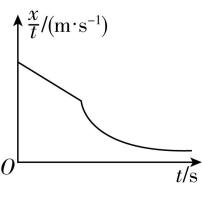
D.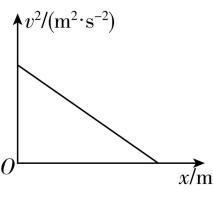
答案:BD
解析:近似认为汽车在刹车时做匀减速直线运动,以初速度方向为正,刹车后的加速度保持不变,且加速度方向为负方向,故 $ \mathrm{B} $ 正确;设刹车时的初速度为 $ {v}_{0} $ ,加速度大小为 $ a $ ,根据位移—时间公式可得 $ x={v}_{0}t-\dfrac{1}{2}a{t}^{2} $ ,整理可得 $ \dfrac{x}{t}={v}_{0}-\dfrac{1}{2}at $ ,可知刹车过程的 $ x-t $ 图像为抛物线, $ \dfrac{x}{t}-t $ 图像为斜率为负的倾斜直线,故 $ \mathrm{A} $ 、 $ \mathrm{C} $ 错误;根据位移—速度公式可得 $ {v}^{2}-{v}_{0}^{2}=-2ax $ ,可得 $ {v}^{2}={v}_{0}^{2}-2ax $ ,可知 $ {v}^{2}-x $ 图像为斜率为负的倾斜直线,故 $ \mathrm{D} $ 正确.
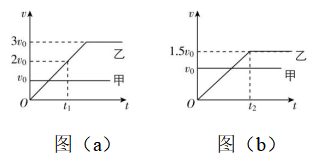
10.甲、乙两质点从同一位置同时开始沿同一方向做直线运动,甲做速度为 $ {v}_{0} $ 的匀速直线运动,乙由静止开始先做匀加速直线运动,当其速度达到 $ {v}_{1} $ 后改做匀速直线运动,当乙追上甲时乙的速度为 $ {v}_{2} $ .则( )(多选)
A.若 $ {v}_{1}=3{v}_{0} $ ,则 $ {v}_{2}=2{v}_{0} $
B.若 $ {v}_{1}=3{v}_{0} $ ,则 $ {v}_{2} $ 可能等于 $ 3{v}_{0} $
C.若 $ {v}_{1}=1.5{v}_{0} $ ,则 $ {v}_{2}=1.5{v}_{0} $
D.若 $ {v}_{1}=1.8{v}_{0} $ ,则 $ {v}_{2} $ 可能等于 $ 1.5{v}_{0} $
答案:AC
解析:若 $ {v}_{1}=3{v}_{0} $ ,甲、乙的 $ v-t $ 图像如图(a)所示,由图(a)可知,乙在 $ {t}_{1} $ 时刻追上甲,追上时乙的速度为 $ 2{v}_{0} $ ,故 $ \mathrm{A} $ 正确, $ \mathrm{B} $ 错误;若 $ {v}_{1}=1.5{v}_{0} $ ,甲、乙的 $ v-t $ 图像如图(b)所示,由图(b)知 $ {t}_{2} $ 时刻,乙的速度等于 $ 1.5{v}_{0} $ ,此时乙的位移小于甲的位移, $ {t}_{2} $ 时刻以后乙以 $ 1.5{v}_{0} $ 的速度做匀速运动,追上甲时乙的速度为 $ 1.5{v}_{0} $ ,故 $ \mathrm{C} $ 正确,同理可知, $ \mathrm{D} $ 错误.
11.为了研究汽车的启动和制动性能,现用甲、乙两辆完全相同的汽车在平直公路上分别进行实验.让甲车以加速度 $ {a}_{1} $ 加速到最大速度后匀速运动,一段时间后再以加速度 $ {a}_{2} $ 制动,直到停止;乙车以最大加速度 $ {a}_{1} $ 加速到最大速度后立即以加速度 $ \dfrac{{a}_{2}}{2} $ 制动,直到停止.实验测得甲、乙两车的运动时间相等,且两车运动的位移之比为 $ 7:5. $ 则( )(多选)
A.甲加速的时间和甲减速的时间之比为 $ 1:2 $
B.甲加速的时间和甲减速的时间之比为 $ 3:1 $
C. $ {a}_{1}:{a}_{2}=2:1 $
D. $ {a}_{1}:{a}_{2}=1:3 $
答案:AC
解析:解法一:基本公式法
设最大速度为 $ {v}_{ \max } $ ,故乙车运动总时间为 $ {t}_{乙}=\dfrac{{v}_{ \max }}{{a}_{1}}+\dfrac{{v}_{ \max }}{\dfrac{{a}_{2}}{2}}=\dfrac{{v}_{ \max }}{{a}_{1}}+\dfrac{2{v}_{ \max }}{{a}_{2}} $ ,甲车加速与减速的总时间 $ {t}_{甲变}=\dfrac{{v}_{ \max }}{{a}_{1}}+\dfrac{{v}_{ \max }}{{a}_{2}} $ ,故甲车匀速运动的时间为 $ {t}_{甲匀}={t}_{乙}-{t}_{甲变}=\dfrac{{v}_{ \max }}{{a}_{2}} $ , $ {x}_{甲}=\dfrac{{v}_{ \max }}{2}{t}_{甲变}+{v}_{ \max }{t}_{甲匀}=\dfrac{{v}_{ \max }^{2}}{2}\cdot (\dfrac{1}{{a}_{1}}+\dfrac{3}{{a}_{2}}) $ , $ {x}_{乙}=\dfrac{{v}_{ \max }}{2}{t}_{乙}=\dfrac{{v}_{ \max }^{2}}{2}(\dfrac{1}{{a}_{1}}+\dfrac{2}{{a}_{2}}) $ ,又 $ \dfrac{{x}_{甲}}{{x}_{乙}}=\dfrac{7}{5} $ ,联立解得 $ {a}_{1}=2{a}_{2} $ ,故 $ \dfrac{{t}_{甲加}}{{t}_{甲减}}=\dfrac{\dfrac{{v}_{ \max }}{{a}_{1}}}{\dfrac{{v}_{ \max }}{{a}_{2}}}=\dfrac{1}{2} $ , $ \mathrm{A} $ 、 $ \mathrm{C} $ 正确.
解法二:图像法
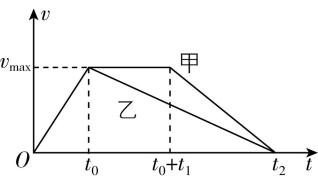
根据题意画出 $ v-t $ 图像,如图所示,甲的位移 $ {x}_{1}=\dfrac{({t}_{1}+{t}_{2}){v}_{ \max }}{2} $ ,乙的位移 $ {x}_{2}=\dfrac{{v}_{ \max }{t}_{2}}{2} $ ,两车运动的位移之比为 $ 7:5 $ ,则 $ \dfrac{{t}_{1}}{{t}_{2}}=\dfrac{2}{5} $ ,因为甲车减速时的加速度为 $ {a}_{2} $ ,乙车减速时的加速度为 $ \dfrac{{a}_{2}}{2} $ ,所以乙车匀减速时间是甲车匀减速时间的2倍,则甲车匀减速运动和匀速运动的时间相等,因此甲车加速的时间和减速的时间之比为 $ 1:2 $ ,故 $ {a}_{1}:{a}_{2}=2:1 $ ,故 $ \mathrm{A} $ 、 $ \mathrm{C} $ 正确.






 (多选)
(多选)






