10.某中学为研究本校高一学生在联考中的数学成绩,随机抽取了100位同学的数学成绩作为样本,得到以 $ [80,90) $ , $ [90,100) $ , $ [100,110) $ , $ [110,120) $ , $ [120,130) $ , $ [130,140] $ 分组的样本频率分布直方图,如图所示.
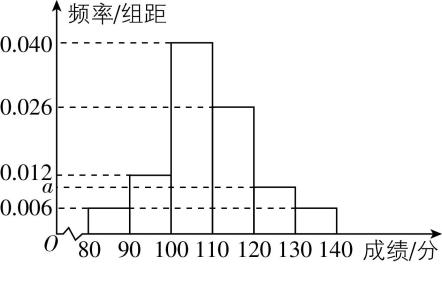
(1) 求直方图中 $ a $ 的值,并估计本次联考该校数学成绩的中位数;
(2) 现在从分数在 $ [80,90) $ 和 $ [90,100) $ 的学生中采用比例分配的分层随机抽样的方法共抽取6人,再从这6人中随机抽取2人,求抽取的两人恰好一人分数在 $ [80,90) $ 内,另一人分数在 $ [90,100) $ 内的概率.
(1) 【解】由频率分布直方图可得 $ (0.006+0.012+0.04+0.026+a+0.006)×10=1 $ ,
解得 $ a=0.01 $ .本次联考该校数学成绩在 $ [80,90) $ 的频率为 $ 0.006×10=0.06 $ ,
在 $ [90,100) $ 的频率为 $ 0.012×10=0.12 $ ,在 $ [100,110) $ 的频率为 $ 0.04×10=0.4 $ ,
因为 $ 0.06+0.12=0.18 < 0.5 $ , $ 0.06+0.12+0.4=0.58 > 0.5 $ ,
所以中位数在 $ [100,110) $ 之间,设为 $ m $ ,则 $ 0.06+0.12+(m-100)×0.04=0.5 $ ,
解得 $ m=108 $ .所以估计本次联考该校数学成绩的中位数为108.
(2) 成绩在 $ [80,90) $ 的人数与成绩在 $ [90,100) $ 的人数的频率之比为 $ 1:2 $ ,
根据比例分配的分层随机抽样可知抽取的6人中成绩在 $ [80,90) $ 的有2人,成绩在 $ [90,100) $ 的有4人.
假设成绩在 $ [80,90) $ 的2人分别记为 $ {A}_{1} $ , $ {A}_{2} $ ,成绩在 $ [90,100) $ 的4人分别记为 $ {B}_{1} $ , $ {B}_{2} $ , $ {B}_{3} $ , $ {B}_{4} $ ,则随机抽取2人的样本空间为
$ {({A}_{1},{A}_{2}) $ , $ ({A}_{1},{B}_{1}) $ , $ ({A}_{1},{B}_{2}) $ , $ ({A}_{1},{B}_{3}) $ , $ ({A}_{1},{B}_{4}) $ , $ ({A}_{2},{B}_{1}) $ , $ ({A}_{2},{B}_{2}) $ , $ ({A}_{2},{B}_{3}) $ ,
$ ({A}_{2},{B}_{4}) $ , $ ({B}_{1},{B}_{2}) $ , $ ({B}_{1},{B}_{3}) $ , $ ({B}_{1},{B}_{4}) $ , $ ({B}_{2},{B}_{3}) $ , $ ({B}_{2},{B}_{4}) $ , $ ({B}_{3},{B}_{4})} $ ,共15个.
则抽取的2人中恰好一人分数在 $ [80,90) $ 内,另一人分数在 $ [90,100) $ 内的样本点有 $ ({A}_{1},{B}_{1}) $ , $ ({A}_{1},{B}_{2}) $ , $ ({A}_{1},{B}_{3}) $ , $ ({A}_{1},{B}_{4}) $ , $ ({A}_{2},{B}_{1}) $ , $ ({A}_{2},{B}_{2}) $ , $ ({A}_{2},{B}_{3}) $ , $ ({A}_{2},{B}_{4}) $ ,共8个,
所以所求概率 $ P=\dfrac{8}{15} $ .