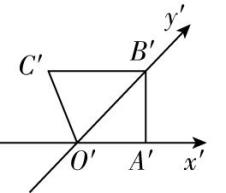
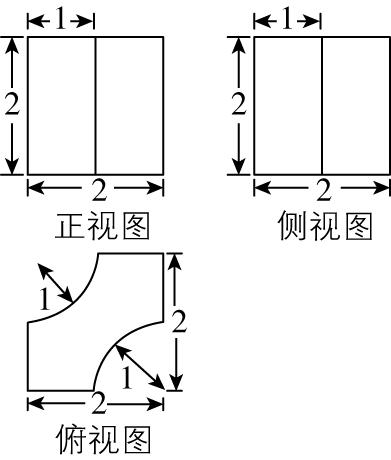
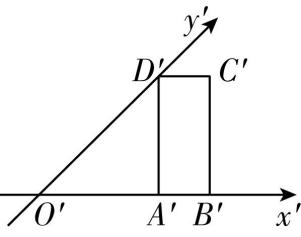
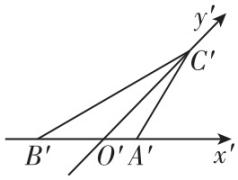
解析:由余弦定理,可得 $ B^\prime D{\prime }^{2}=A^\prime D{\prime }^{2}+A^\prime B{\prime }^{2}-2A\prime D^\prime \cdot A^\prime B^\prime \cos \dfrac{\mathrm{\pi }}{4} $ ,
即 $ A^\prime B{\prime }^{2}-2A\prime B^\prime -3=0 $ ,解得 $ A^\prime B^\prime =3 $ 或 $ A^\prime B^\prime =-1 $ (舍去),故 $ \mathrm{A} $ 错误;
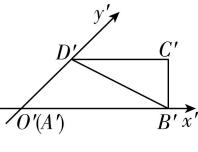
在直角梯形中, $ C^\prime D^\prime =A^\prime B^\prime -A^\prime D^\prime × \cos \dfrac{\mathrm{\pi }}{4}=3-1=2 $ , $ B^\prime C^\prime =A^\prime D^\prime \sin \dfrac{\mathrm{\pi }}{4}=\sqrt{2}×\dfrac{\sqrt{2}}{2}=1 $ ,由斜二测画法知, $ CD=C^\prime D^\prime =2 $ ,故 $ \mathrm{B} $ 正确;
因为直角梯形 $ A^\prime B^\prime C^\prime D^\prime $ 的面积为 $ \dfrac{(2+3)×1}{2}=\dfrac{5}{2} $ ,所以四边形 $ ABCD $ 的面积为 $ \dfrac{\dfrac{5}{2}}{\dfrac{\sqrt{2}}{4}}=5\sqrt{2} $ ,故 $ \mathrm{C} $ 正确;
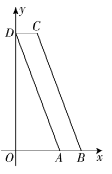
由斜二测画法可知,四边形 $ ABCD $ 为直角梯形,其中 $ \mathrm{\angle }CDA=\mathrm{\angle }DAB=\dfrac{\mathrm{\pi }}{2} $ , $ AB=3 $ , $ CD=2 $ , $ AD=2A\prime D^\prime =2\sqrt{2} $ ,
所以 $ BC=\sqrt{A{D}^{2}+(AB-CD)^{2}}=\sqrt{8+1}=3 $ ,
所以 $ \sin \mathrm{\angle }BCD= \sin \mathrm{\angle }ABC=\dfrac{AD}{BC}=\dfrac{2\sqrt{2}}{3} $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{C}\mathrm{D} $ .

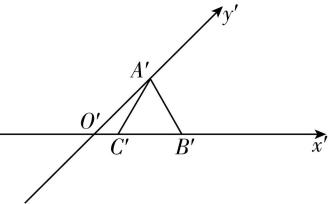
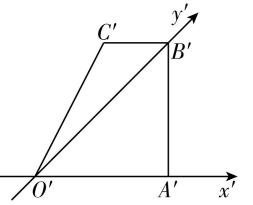
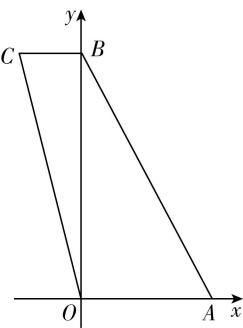
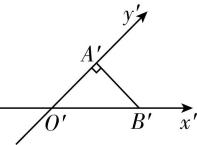
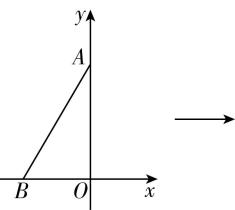
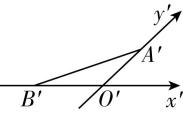
 (多选)
(多选)