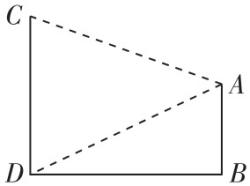
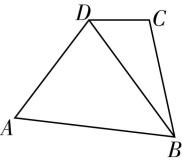
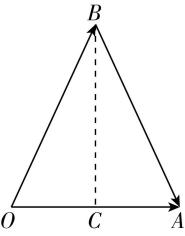
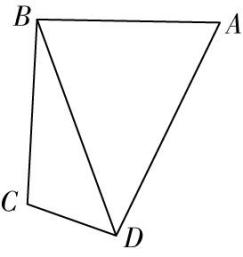
11.某社区规划在小区内修建一个如图所示的四边形休闲区.已知 $ BC=2CD=20 $ 米,且修建该休闲区的费用是200元/平方米,则下列结论正确的是( )
B.若 $ BD=10\sqrt{7} $ 米,且四边形 $ ABCD $ 的四个顶点共圆,则 $ △ABD $ 的面积的最大值为 $ 350\sqrt{3} $ 平方米
C.若 $ AB=20 $ 米, $ AD=30 $ 米, $ A+C=\dfrac{2\mathrm{\pi }}{3} $ ,则该社区修建该休闲区的修建费用为6万元
D.若 $ BD\perp AB $ ,且 $ BD=AB $ ,当 $ \mathrm{\angle }BCD $ 变化时, $ AC $ 长度的最大值为 $ 10(2\sqrt{2}+1) $ 米
解析:对于 $ \mathrm{A} $ ,在 $ △ABD $ 和 $ △BCD $ 中,由余弦定理得 $ B{D}^{2}=A{B}^{2}+A{D}^{2}-2AB\cdot AD\cdot \cos A=B{C}^{2}+C{D}^{2}-2BC\cdot CD\cdot \cos C $ ,
即 $ B{D}^{2}=1300-1200 \cos A=500-400 \cos C $ ,所以 $ 3 \cos A- \cos C=2 $ ,
又四边形 $ ABCD $ 的四个顶点共圆,所以 $ A+C=\mathrm{\pi } $ ,所以 $ \cos A+ \cos C=0 $ ,即 $ \cos C=- \cos A $ ,所以 $ 3 \cos A+ \cos A=2 $ ,
所以 $ \cos A=\dfrac{1}{2} $ .
又 $ 0 < A < \mathrm{\pi } $ ,所以 $ A=\dfrac{\mathrm{\pi }}{3} $ ,所以 $ C=\dfrac{2\mathrm{\pi }}{3} $ ,所以 $ B{D}^{2}=1300-1200×\dfrac{1}{2}=700 $ ,
所以 $ BD=10\sqrt{7} $ ,故 $ \mathrm{A} $ 正确;
对于 $ \mathrm{B} $ ,在 $ △BCD $ 中,由余弦定理得 $ B{D}^{2}=B{C}^{2}+C{D}^{2}-2BC\cdot CD\cdot \cos C=400+100-400 \cos C=700 $ ,
所以 $ \cos C=-\dfrac{1}{2} $ ,又 $ 0 < C < \mathrm{\pi } $ ,所以 $ C=\dfrac{2\mathrm{\pi }}{3} $ ,
若 $ A $ , $ B $ , $ C $ , $ D $ 四点共圆,则四边形对角互补,即 $ A=\dfrac{\mathrm{\pi }}{3} $ ,在 $ △ABD $ 中,由余弦定理得 $ B{D}^{2}=A{B}^{2}+A{D}^{2}-2AB\cdot AD\cdot \cos A=A{B}^{2}+A{D}^{2}-AB\cdot AD=700 $ ,
所以 $ 700=A{B}^{2}+A{D}^{2}-AB\cdot AD\geqslant 2AB\cdot AD-AB\cdot AD=AB\cdot AD $ ,
当且仅当 $ AB=AD $ 时,等号成立,
所以 $ {S}_{△ABD}=\dfrac{1}{2}AB\cdot AD \sin \dfrac{\mathrm{\pi }}{3}\leqslant \dfrac{700}{2}\cdot \dfrac{\sqrt{3}}{2}=175\sqrt{3} $ ,故 $ \mathrm{B} $ 错误.
对于 $ \mathrm{C} $ ,由选项 $ \mathrm{A} $ 知 $ 3 \cos A- \cos C=2① $ ,
$ △BCD $ 的面积为 $ \dfrac{1}{2}BC\cdot CD\cdot \sin C=\dfrac{1}{2}×20×10× \sin C=100 \sin C $ ,
$ △ABD $ 的面积为 $ \dfrac{1}{2}AB\cdot AD\cdot \sin A=\dfrac{1}{2}×20×30× \sin A=300 \sin A $ ,
所以四边形 $ ABCD $ 的面积为 $ 300 \sin A+100 \sin C $ ,
设 $ 3 \sin A+ \sin C=t(t > 0)② $ ,则 $ {①}^{2}+{②}^{2} $ 得 $ {t}^{2}+4=9+1-6 \cos (A+C) $ ,
所以 $ {t}^{2}=6-6 \cos (A+C) $ ,又 $ A+C=\dfrac{2\mathrm{\pi }}{3} $ ,所以 $ {t}^{2}=9 $ ,又 $ t > 0 $ ,所以 $ t=3 $ ,
所以四边形 $ ABCD $ 的面积为300平方米,所以修建该休闲区的总费用为6万元,故 $ \mathrm{C} $ 正确;
对于 $ \mathrm{D} $ ,设 $ \mathrm{\angle }BCD=\theta (0 < \theta < \mathrm{\pi }) $ ,在 $ △BCD $ 中,由余弦定理得 $ B{D}^{2}=B{C}^{2}+C{D}^{2}-2BC\cdot CD\cdot \cos \theta =500-400 \cos \theta $ ,
则 $ BD=10\sqrt{5-4 \cos \theta } $ ,所以 $ AB=10\sqrt{5-4 \cos \theta } $ ,在 $ △BCD $ 中,由正弦定理得 $ \dfrac{CD}{ \sin \mathrm{\angle }CBD}=\dfrac{BD}{ \sin \mathrm{\angle }BCD} $ ,即 $ \dfrac{10}{ \sin \mathrm{\angle }CBD}=\dfrac{10\sqrt{5-4 \cos \theta }}{ \sin \theta } $ ,
所以 $ \sin \mathrm{\angle }CBD=\dfrac{ \sin \theta }{\sqrt{5-4 \cos \theta }} $ ,
在 $ △ABC $ 中,由余弦定理得 $ AC $
$ =\sqrt{B{C}^{2}+A{B}^{2}-2BC\cdot AB\cdot \cos (\mathrm{\angle }CBD+\dfrac{\mathrm{\pi }}{2})} $
$ =\sqrt{400+500-400 \cos \theta +400 \sin \theta } $
$ =\sqrt{900-400 \cos \theta +400 \sin \theta } $
$ =\sqrt{900+400\sqrt{2} \sin (\theta -\dfrac{\mathrm{\pi }}{4})} $
$ \leqslant \sqrt{900+400\sqrt{2}}=10(2\sqrt{2}+1) $ ,
当 $ \sin (\theta -\dfrac{\mathrm{\pi }}{4})=1 $ ,即 $ \theta =\dfrac{3\mathrm{\pi }}{4} $ 时,等号成立,故 $ \mathrm{D} $ 正确.
故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .
 (多选)
(多选)