专题4 解三角形中的最值及范围问题

1．设 $ △ABC $ 的内角 $ A $ , $ B $ , $ C $ 的对边分别为 $ a $ , $ b $ , $ c $ .若 $ a=\sqrt{2} $ ， $ \mathrm{ \cos }A=\dfrac{1}{3} $ ，则 $ b+c $ 的最大值为（）

A．1

B． $ \sqrt{3} $

C．2

D． $ \sqrt{6} $

答案：D

解析：

由余弦定理 $ {a}^{2}={b}^{2}+{c}^{2}-2bc \cos A $ ,及 $ a=\sqrt{2} $ , $ \cos A=\dfrac{1}{3} $ ,

得 $ 2={b}^{2}+{c}^{2}-\dfrac{2}{3}bc $ .根据完全平方公式 $ (b+c)^{2}={b}^{2}+2bc+{c}^{2} $ ,得 $ {b}^{2}+{c}^{2}={\left(b+c\right) ^ {2}}-2bc $ ,将其代入上式可得 $ 2={\left(b+c\right) ^ {2}}-2bc-\dfrac{2}{3}bc={\left(b+c\right) ^ {2}}-\dfrac{8}{3}bc $ .

因为 $ bc\leqslant {\left(\dfrac{b+c}{2}\right) ^ {2}} $ （当且仅当 $ b=c $ 时取等号）,所以 $ -\dfrac{8}{3}bc\geqslant -\dfrac{8}{3}{\left(\dfrac{b+c}{2}\right) ^ {2}} $ ,则 $ 2= (b+c)^{2}-\dfrac{8}{3}bc\geqslant (b+c)^{2}-\dfrac{8}{3}{\left(\dfrac{b+c}{2} \right) ^ {2}}=\dfrac{1}{3} (b+c)^{2} $ ,得 $ (b+c)^{2}\leqslant 6 $ ,即 $ 0 < b+c\leqslant \sqrt{6} $ .所以 $ b+c $ 的最大值为 $ \sqrt{6} $ .故选 $ \mathrm{D} $ .

2．在 $ △ABC $ 中，内角 $ A $ , $ B $ , $ C $ 的对边分别为 $ a $ , $ b $ , $ c $ ，若 $ A=B+2C $ , $ b+c=1 $ ，则 $ a $ 的最小值为（）

A． $ \dfrac{2\sqrt{2}}{5} $

B． $ \dfrac{2}{5} $

C． $ \dfrac{3}{5} $

D． $ \dfrac{4}{5} $

答案：D

解析：

由题可得 $ B=\dfrac{\mathrm{\pi }-3C}{2} $ , $ A=\dfrac{\mathrm{\pi }+C}{2} $ ,且 $ 0 < C < \dfrac{\mathrm{\pi }}{3} $ .由正弦定理可得 $ \dfrac{a}{ \sin A}=\dfrac{b}{ \sin B}=\dfrac{c}{ \sin C}=\dfrac{b+c}{ \sin B+ \sin C}=\dfrac{1}{ \sin B+ \sin C} $ ,所以 $ a=\dfrac{ \sin \dfrac{\mathrm{\pi }+C}{2}}{ \sin \dfrac{\mathrm{\pi }-3C}{2}+ \sin C}=\dfrac{ \cos \dfrac{C}{2}}{ \cos \dfrac{3C}{2}+ \sin C} $ .

因为 $ \cos \dfrac{3C}{2}= \cos \dfrac{C}{2} \cos C- \sin \dfrac{C}{2} \sin C= \cos \dfrac{C}{2} \cos C-2{ \sin }^{2}\frac{C}{2}\cdot \cos \dfrac{C}{2} $ ,所以 $ a=\dfrac{ \cos \dfrac{C}{2}}{ \cos \dfrac{C}{2} \cos C-2{ \sin }^{2}\frac{C}{2} \cos \dfrac{C}{2}+2 \sin \dfrac{C}{2} \cos \dfrac{C}{2}} $

$ =\dfrac{1}{ \cos C-2{ \sin }^{2}\frac{C}{2}+2 \sin \dfrac{C}{2}} $

$ =\dfrac{1}{-4{ \sin }^{2}\frac{C}{2}+2 \sin \dfrac{C}{2}+1} $ ,令 $ t= \sin \dfrac{C}{2} $ ,则 $ t\in (0,\dfrac{1}{2}) $ ,则 $ a=\dfrac{1}{-4{t}^{2}+2t+1}=\dfrac{1}{\dfrac{5}{4}-4{\left(t-\dfrac{1}{4}\right) ^ {2}}}\geqslant \dfrac{4}{5} $ ,当且仅当 $ t=\dfrac{1}{4} $ ,即 $ \sin \dfrac{C}{2}=\dfrac{1}{4} $ 时, $ a $ 取得最小值 $ \dfrac{4}{5} $ ,故选 $ \mathrm{D} $ .

3．如图，在等边三角形 $ ABC $ 中， $ AB=2 $ ，点 $ M $ ， $ N $ 是边 $ BC $ 上的两动点（点 $ M $ 在 $ N $ 的左边），满足 $ \mathrm{\angle }MAN=\dfrac{\mathrm{\pi }}{6} $ ，记 $ \mathrm{\angle }BAM=\theta $ .

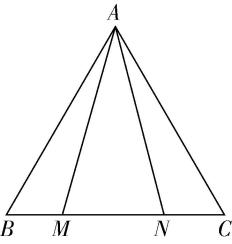
试题资源网 https://stzy.com

（1）若 $ \mathrm{ \sin }\theta =\dfrac{1}{2} $ ，求 $ MN $ 的长；

（2）求 $ MN $ 的最小值.

答案：

（1）【解】 $ \because \sin \theta =\dfrac{1}{2} $ , $ 0\leqslant \theta \leqslant \dfrac{\mathrm{\pi }}{6} $ , $ \therefore \theta =\dfrac{\mathrm{\pi }}{6} $ .

易知此时 $ △ABM $ 为直角三角形, $ M $ 为 $ BC $ 的中点, $ N $ 与 $ C $ 重合, $ \therefore MN=1 $ .

（2）在 $ △ABM $ 中, $ \because \dfrac{AB}{ \sin \mathrm{\angle }AMB}=\dfrac{BM}{ \sin \mathrm{\angle }BAM} $ , $ \therefore BM=\dfrac{2 \sin \theta }{ \sin (\theta +\dfrac{\mathrm{\pi }}{3})} $ ,

在 $ △ABN $ 中, $ \because \dfrac{AB}{ \sin \mathrm{\angle }ANB}=\dfrac{BN}{ \sin \mathrm{\angle }BAN} $ ,

$ \therefore BN=\dfrac{2 \sin (\theta +\dfrac{\mathrm{\pi }}{6})}{ \cos \theta } $ .

$ \because MN=BN-BM=\dfrac{2 \sin (\theta +\dfrac{\mathrm{\pi }}{6})}{ \cos \theta }-\dfrac{2 \sin \theta }{ \sin (\theta +\dfrac{\mathrm{\pi }}{3})}=1+\dfrac{\sqrt{3} \sin \theta }{ \cos \theta }-\dfrac{4 \sin \theta }{ \sin \theta +\sqrt{3} \cos \theta } $ ,

令 $ t=\dfrac{ \sin \theta }{ \cos \theta }(0\leqslant \theta \leqslant \dfrac{\mathrm{\pi }}{6}) $ ,则 $ t\in [0,\dfrac{\sqrt{3}}{3}] $ ,

$ \therefore MN=1+\sqrt{3}t-\dfrac{4t}{t+\sqrt{3}}=\dfrac{4\sqrt{3}}{t+\sqrt{3}}+\sqrt{3}(t+\sqrt{3})-6\geqslant 2\sqrt{12}-6=4\sqrt{3}-6 $ ,

当且仅当 $ \dfrac{4\sqrt{3}}{t+\sqrt{3}}=\sqrt{3}(t+\sqrt{3}) $ ,即 $ t=2-\sqrt{3} $ 时取等号.

$ \therefore MN $ 的最小值为 $ 4\sqrt{3}-6 $ .

解析：

4． $ △ABC $ 的内角 $ A $ ， $ B $ ， $ C $ 所对的边分别是 $ a $ ， $ b $ ， $ c $ ，已知 $ \dfrac{\mathrm{ \cos }C}{c}+\dfrac{\mathrm{ \cos }B}{b}=\dfrac{2-\sqrt{3}}{a} $ ，则 $ A $ 的最大值为（）

A． $ \dfrac{\mathrm{\pi }}{6} $

B． $ \dfrac{\mathrm{\pi }}{3} $

C． $ \dfrac{2\mathrm{\pi }}{3} $

D． $ \dfrac{5\mathrm{\pi }}{6} $

答案：A

解析：

已知 $ \dfrac{ \cos C}{c}+\dfrac{ \cos B}{b}=\dfrac{2-\sqrt{3}}{a} $ ,

则 $ \dfrac{{a}^{2}+{b}^{2}-{c}^{2}}{2abc}+\dfrac{{a}^{2}+{c}^{2}-{b}^{2}}{2abc}=\dfrac{2-\sqrt{3}}{a} $ ,整理得 $ {a}^{2}=(2-\sqrt{3})bc $ .

由余弦定理得 $ \cos A=\dfrac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}\geqslant \dfrac{2bc-(2-\sqrt{3})bc}{2bc}=\dfrac{\sqrt{3}}{2} $ ,当且仅当 $ b=c $ 时取等号,所以 $ \cos A\geqslant \dfrac{\sqrt{3}}{2} $ ,又 $ 0 < A < \mathrm{\pi } $ ,故 $ 0 < A\leqslant \dfrac{\mathrm{\pi }}{6} $ .故选 $ \mathrm{A} $ .

5．已知在 $ △ABC $ 中，点 $ A $ 在 $ BC $ 上的射影 $ H $ 落在线段 $ BC $ 上（不含端点），且满足 $ {AH}^{2}=\dfrac{1}{2}AB\cdot AC $ ，则角 $ A $ 的取值范围是（）

A． $ (\dfrac{\mathrm{\pi }}{3},\dfrac{\mathrm{\pi }}{2}] $

B． $ (\dfrac{\mathrm{\pi }}{3},\dfrac{2\mathrm{\pi }}{3}) $

C． $ (\dfrac{\mathrm{\pi }}{4},\dfrac{\mathrm{\pi }}{2}] $

D． $ (\dfrac{\mathrm{\pi }}{4},\dfrac{3\mathrm{\pi }}{4}) $

答案：A

解析：

在 $ △ABC $ 中,因为 $ A $ 在 $ BC $ 上的射影 $ H $ 落在线段 $ BC $ 上（不含端点）,

所以 $ AH\perp BC $ ,且角 $ B $ , $ C $ 均为锐角.因为 $ AH\cdot BC=AB\cdot AC\cdot \sin A $ ,所以 $ AH=\dfrac{AB\cdot AC\cdot \sin A}{BC} $ .因为 $ A{H}^{2}=\dfrac{1}{2}AB\cdot AC $ ,所以 $ {\left(\dfrac{AB\cdot AC\cdot \sin A}{BC}\right) ^ {2}}=\dfrac{1}{2}AB\cdot AC $ ,

化简得 $ B{C}^{2}=2AB\cdot AC\cdot { \sin }^{2}A $ ,记 $ △ABC $ 中内角 $ A $ , $ B $ , $ C $ 的对边分别为 $ a $ , $ b $ , $ c $ ，则 $ {a}^{2}=2bc{ \sin }^{2}A $ .

因为 $ {a}^{2}={b}^{2}+{c}^{2}-2bc \cos A $ ,且 $ {b}^{2}+{c}^{2}\geqslant 2bc $ ,

所以 $ 2bc{ \sin }^{2}A={b}^{2}+{c}^{2}-2bc \cos A\geqslant 2bc(1- \cos A) $ ,当且仅当 $ b=c $ 时取等号,则有 $ { \sin }^{2}A\geqslant 1- \cos A $ ,即 $ { \cos }^{2}A\leqslant \cos A $ ,所以 $ 0\leqslant \cos A < 1 $ ,即 $ A\in (0,\dfrac{\mathrm{\pi }}{2}] $ .

若 $ b=c $ ,此时 $ \cos A=0 $ ,即 $ A=\dfrac{\mathrm{\pi }}{2} $ .

若 $ b\ne c $ ,不妨设 $ b > c $ ,则 $ \cos B=\dfrac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac} > 0 $ ,即 $ {a}^{2} > {b}^{2}-{c}^{2} $ ,

所以 $ {a}^{2}={b}^{2}+{c}^{2}-2bc \cos A=2bc{ \sin }^{2}A > {b}^{2}-{c}^{2} $ ,即 $ \cos A < \dfrac{c}{b} < 1 $ .

因为 $ {b}^{2}+{c}^{2}=2bc{ \sin }^{2}A+2bc \cos A $ ,

即 $ 2({ \sin }^{2}A+ \cos A)=\dfrac{b}{c}+\dfrac{c}{b} $ ,

函数 $ y=x+\dfrac{1}{x} $ 在区间 $ (0,1) $ 上单调递减,所以 $ \dfrac{c}{b}+\dfrac{b}{c} < \cos A+\dfrac{1}{ \cos A} $ ,即 $ 2({ \sin }^{2}A+ \cos A) < \cos A+\dfrac{1}{ \cos A} $ ,化简可得 $ 2{ \sin }^{2}A < \dfrac{1-{ \cos }^{2}A}{ \cos A} $ ,即 $ \cos A < \dfrac{1}{2} $ ,得 $ A > \dfrac{\mathrm{\pi }}{3} $ ,所以角 $ A $ 的取值范围是 $ (\dfrac{\mathrm{\pi }}{3},\dfrac{\mathrm{\pi }}{2}] $ .故选 $ \mathrm{A} $ .

6．在锐角三角形 $ ABC $ 中，内角 $ A $ ， $ B $ ， $ C $ 的对边分别为 $ a $ ， $ b $ ， $ c $ ，若 $ { \sin }^{2}B={ \sin }^{2}A+ \sin A \sin C $ ，则 $ \tan A \tan B $ 的取值范围为 .

答案：

$ (1,+\mathrm{\infty }) $

解析：

由正弦定理角化边得 $ {b}^{2}=a(a+c) $ ,由 $ \cos B=\dfrac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}=\dfrac{{a}^{2}+{c}^{2}-a(a+c)}{2ac}=\dfrac{c}{2a}-\dfrac{1}{2} $ ；

$ \cos A=\dfrac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}=\dfrac{a(a+c)+{c}^{2}-{a}^{2}}{2bc}=\dfrac{a+c}{2b} $ .

因为 $ △ABC $ 为锐角三角形,所以 $ A $ , $ B\in (0,\dfrac{\mathrm{\pi }}{2}) $ , $ 2A\in (0,\mathrm{\pi }) $ ,

所以 $ \cos 2A=2{ \cos }^{2}A-1=\dfrac{2 (a+c)^{2}}{4{b}^{2}}-1=\dfrac{{\left(a+c \right) ^ {2}}}{2a (a+c )}-1=\dfrac{c}{2a}-\dfrac{1}{2} $ .

所以 $ \cos B= \cos 2A $ ,所以 $ B=2A $ ,所以 $ C=\mathrm{\pi }-3A $ .

因为 $ △ABC $ 为锐角三角形,

所以 $ \begin{cases}0 < A < \dfrac{\mathrm{\pi }}{2},\\ 0 < 2A < \dfrac{\mathrm{\pi }}{2},\\ 0 < \mathrm{\pi }-3A < \dfrac{\mathrm{\pi }}{2},\end{cases} $ 解得 $ \dfrac{\mathrm{\pi }}{6} < A < \dfrac{\mathrm{\pi }}{4} $ .

设 $ \tan A=t $ ,则 $ t\in (\dfrac{\sqrt{3}}{3},1) $ , $ \tan A \tan B=t\cdot \dfrac{2t}{1-{t}^{2}}=\dfrac{2}{\dfrac{1}{{t}^{2}}-1}\in (1,+\mathrm{\infty }) $ .

7．在锐角三角形 $ ABC $ 中，内角 $ A $ ， $ B $ ， $ C $ 的对边分别是 $ a $ , $ b $ , $ c $ ，且 $ b\mathrm{ \sin }B+b\mathrm{ \sin }C\mathrm{ \cos }A+a\mathrm{ \sin }C\mathrm{ \cos }B=a\mathrm{ \sin }A+c\mathrm{ \sin }B $ .

（1）求角 $ A $ 的大小；

（2）求 $ 2\mathrm{ \cos }B+ \cos C $ 的取值范围.

答案：

（1）【解】因为 $ b \sin B+b \sin C \cos A+a\cdot \sin C \cos B=a \sin A+c \sin B $ ,

所以由正弦定理可得 $ {b}^{2}+bc \cos A+ac\cdot \cos B={a}^{2}+bc $ ,

再由余弦定理可得 $ {b}^{2}+\dfrac{{b}^{2}+{c}^{2}-{a}^{2}}{2}+\dfrac{{a}^{2}+{c}^{2}-{b}^{2}}{2}={a}^{2}+bc $ ,即 $ {b}^{2}+{c}^{2}={a}^{2}+bc $ ,

所以 $ \cos A=\dfrac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}=\dfrac{bc}{2bc}=\dfrac{1}{2} $ .

因为 $ 0 < A < \mathrm{\pi } $ ,所以 $ A=\dfrac{\mathrm{\pi }}{3} $ .

（2）因为 $ A=\dfrac{\mathrm{\pi }}{3} $ ,所以 $ B+C=\dfrac{2\mathrm{\pi }}{3} $ ,所以 $ C=\dfrac{2\mathrm{\pi }}{3}-B $ ,则 $ 2\mathrm{ \cos }B+ \cos C=2\mathrm{ \cos }B+ \cos (\dfrac{2\mathrm{\pi }}{3}-B )=\dfrac{3}{2}\mathrm{ \cos }B+\dfrac{\sqrt{3}}{2}\mathrm{ \sin }B=\sqrt{3}\mathrm{ \sin (}B+\dfrac{\mathrm{\pi }}{3} ) $ .

因为 $ △ABC $ 是锐角三角形,所以 $ \begin{cases}0 < B < \dfrac{\mathrm{\pi }}{2},\\ 0 < \dfrac{2\mathrm{\pi }}{3}-B < \dfrac{\mathrm{\pi }}{2},\end{cases} $ 解得 $ \dfrac{\mathrm{\pi }}{6} < B < \dfrac{\mathrm{\pi }}{2} $ ,

所以 $ \dfrac{\mathrm{\pi }}{2} < B+\dfrac{\mathrm{\pi }}{3} < \dfrac{5\mathrm{\pi }}{6} $ ,所以 $ \dfrac{1}{2} < \sin (B+\dfrac{\mathrm{\pi }}{3}) < 1 $ ,则 $ \dfrac{\sqrt{3}}{2} < \sqrt{3} \sin (B+\dfrac{\mathrm{\pi }}{3}) < \sqrt{3} $ ,

即 $ 2 \cos B+ \cos C $ 的取值范围是 $ (\dfrac{\sqrt{3}}{2},\sqrt{3}) $ .

解析：

8．在 $ △ABC $ 中，内角 $ A $ ， $ B $ ， $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ ,若 $ 2\mathrm{a}\mathrm{c}\mathrm{o}\mathrm{s}A=b \cos C+\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}B $ , $ a=1 $ ，则 $ △ABC $ 周长的最大值为（）

A．1

B．2

C．3

D． $ \dfrac{\sqrt{3}}{4} $

答案：C

解析：

在 $ △ABC $ 中, $ 2a \cos A=b \cos C+c \cos B=b\cdot \dfrac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}+c\cdot \dfrac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}=a $ ,

得 $ \cos A=\dfrac{1}{2} $ ,则 $ 1={a}^{2}={b}^{2}+{c}^{2}-2bc \cos A= (b+c)^{2}-3bc\geqslant (b+c)^{2}-3{\left(\dfrac{b+c}{2} \right) ^ {2}}=\dfrac{ (b+c)^{2}}{4} $ ,

解得 $ b+c\leqslant 2 $ ,当且仅当 $ b=c=1 $ 时取等号,所以 $ △ABC $ 周长的最大值为3.故选 $ \mathrm{C} $ .

9．在锐角三角形 $ ABC $ 中，内角 $ A $ , $ B $ , $ C $ 所对的边分别为 $ a $ , $ b $ , $ c $ ， $ (4{a}^{2}-2\sqrt{3}ac) \cos B=\sqrt{3}({a}^{2}+{b}^{2}-{c}^{2}) $ ，且 $ a=1 $ ，则 $ △ABC $ 周长的取值范围为 .

答案：

$ (\dfrac{3+\sqrt{3}}{2},\sqrt{3}+1) $

解析：

因为 $ (4{a}^{2}-2\sqrt{3}ac)\cdot \cos B=\sqrt{3}({a}^{2}+{b}^{2}-{c}^{2}) $ ,所以由余弦定理得 $ (4{a}^{2}-2\sqrt{3}ac) \cos B=\sqrt{3}\cdot 2ab \cos C $ ,即 $ (2a-\sqrt{3}c) \cos B=\sqrt{3}b \cos C $ ,

所以由正弦定理得 $ (2 \sin A-\sqrt{3} \sin C)\cdot \cos B=\sqrt{3} \sin B \cos C $ ,

所以 $ 2 \sin A \cos B=\sqrt{3}( \sin C \cos B+ \cos C \sin B)=\sqrt{3} \sin (B+C)=\sqrt{3} \sin A $ .又 $ \sin A\ne 0 $ ,所以 $ \cos B=\dfrac{\sqrt{3}}{2} $ .又 $ △ABC $ 为锐角三角形,所以 $ B=\dfrac{\mathrm{\pi }}{6} $ .

又 $ \dfrac{a}{ \sin A}=\dfrac{b}{ \sin B}=\dfrac{c}{ \sin C} $ ,所以 $ b=\dfrac{a \sin B}{ \sin A}=\dfrac{1}{2 \sin A} $ , $ c=\dfrac{a \sin C}{ \sin A}=\dfrac{ \sin (\dfrac{5\mathrm{\pi }}{6}-A)}{ \sin A}=\dfrac{ \cos A}{2 \sin A}+\dfrac{\sqrt{3}}{2} $ .又 $ 0 < A < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ 0 < \dfrac{A}{2} < \dfrac{\mathrm{\pi }}{4} $ ,所以 $ \cos \dfrac{A}{2}\ne 0 $ ,所以 $ a+b+c=1+\dfrac{1}{2 \sin A}+\dfrac{ \cos A}{2 \sin A}+\dfrac{\sqrt{3}}{2}=\dfrac{2+\sqrt{3}}{2}+\dfrac{1+ \cos A}{2 \sin A}=\dfrac{2+\sqrt{3}}{2}+\dfrac{2{ \cos }^{2}\frac{A}{2}}{4 \sin \dfrac{A}{2} \cos \dfrac{A}{2}}=\dfrac{2+\sqrt{3}}{2}+\dfrac{1}{2 \tan \dfrac{A}{2}} $ .

又 $ \begin{cases}0 < A < \dfrac{\mathrm{\pi }}{2},\\ 0 < C=\dfrac{5\mathrm{\pi }}{6}-A < \dfrac{\mathrm{\pi }}{2},\end{cases} $ 解得 $ \dfrac{\mathrm{\pi }}{3} < A < \dfrac{\mathrm{\pi }}{2} $ ,所以 $ \dfrac{\mathrm{\pi }}{6} < \dfrac{A}{2} < \dfrac{\mathrm{\pi }}{4} $ ,所以 $ \tan \dfrac{A}{2}\in (\dfrac{\sqrt{3}}{3},1) $ .

则 $ a+b+c=\dfrac{2+\sqrt{3}}{2}+\dfrac{1}{2 \tan \dfrac{A}{2}}\in (\dfrac{3+\sqrt{3}}{2},\sqrt{3}+1) $ ,故 $ △ABC $ 周长的取值范围为 $ (\dfrac{3+\sqrt{3}}{2},\sqrt{3}+1) $ .

10．在 $ △ABC $ 中，内角 $ A $ ， $ B $ ， $ C $ 所对的边分别为 $ a $ ， $ b $ ， $ c $ ，设向量 $ \boldsymbol{m}=( \sin A+ \sin B,c) $ , $ \boldsymbol{n}=(a-b, \sin C+ \sin A) $ ，且 $ \boldsymbol{m}\perp \boldsymbol{n} $ .

（1）判断 $ △ABC $ 的形状；

（2）若 $ b=2 $ ，求 $ △ABC $ 周长的最大值.

答案：

（1）【解】由 $ \boldsymbol{m}\perp \boldsymbol{n} $ ,得 $ \boldsymbol{m}\cdot \boldsymbol{n}=( \sin A+ \sin B)(a-b)+c( \sin C+ \sin A)=0 $ ,

所以由正弦定理得 $ (a+b)(a-b)+c(c+a)=0 $ ,即 $ {a}^{2}+{c}^{2}-{b}^{2}=-ac $ ,

所以 $ \cos B=\dfrac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}=\dfrac{-ac}{2ac}=-\dfrac{1}{2} $ .

又 $ B\in (0,\mathrm{\pi }) $ ,所以 $ B=\dfrac{2\mathrm{\pi }}{3} $ ,

所以 $ △ABC $ 为钝角三角形.

（2）由（1）知, $ {a}^{2}+{c}^{2}-{b}^{2}=-ac $ ,

又 $ b=2 $ ,故 $ {a}^{2}+{c}^{2}-4=-ac $ ,即 $ (a+c)^{2}-4=ac $ ,

由基本不等式得 $ ac\leqslant \dfrac{(a+c)^{2}}{4} $ ,即 $ (a+c)^{2}-4\leqslant \dfrac{{\left(a+c \right) ^ {2}}}{4} $ ,

解得 $ a+c\leqslant \dfrac{4\sqrt{3}}{3} $ ,当且仅当 $ a=c=\dfrac{2\sqrt{3}}{3} $ 时等号成立,所以 $ a+b+c\leqslant \dfrac{4\sqrt{3}}{3}+2 $ ,即 $ △ABC $ 周长的最大值为 $ \dfrac{4\sqrt{3}}{3}+2 $ .

解析：

11．在 $ △ABC $ 中，内角 $ A $ ， $ B $ ， $ C $ 所对的边分别为 $ a $ ， $ b $ ， $ c $ ，且 $ a $ ， $ b $ ， $ c $ 满足 $ \dfrac{{b}^{2}+ac}{ac}=\dfrac{ \sin A}{ \sin C}+\dfrac{ \sin C}{ \sin A} $ ， $ c=12 $ .

（1）求 $ B $ ；

（2）若 $ D $ 为线段 $ BC $ 上一点，且满足 $ AD=BD $ ， $ AC=\sqrt{189} $ ，求 $ CD $ 的长；

（3）若 $ △ABC $ 为锐角三角形，求 $ △ABC $ 面积的取值范围.

答案：

（1）【解】由正弦定理可得 $ \dfrac{{b}^{2}+ac}{ac}=\dfrac{a}{c}+\dfrac{c}{a} $ , $ \therefore {b}^{2}={a}^{2}+{c}^{2}-ac $ , $ \therefore \cos B=\dfrac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}=\dfrac{1}{2} $ . $ \because B\in (0,\mathrm{\pi }) $ , $ \therefore B=\dfrac{\mathrm{\pi }}{3} $ .

（2） $ \because D $ 为线段 $ BC $ 上一点,且满足 $ AD=BD $ , $ B=\dfrac{\mathrm{\pi }}{3} $ , $ \therefore △ABD $ 为等边三角形,

$ \therefore \mathrm{\angle }ADC=\dfrac{2\mathrm{\pi }}{3} $ .

设 $ CD=x $ ,在 $ △ADC $ 中, $ A{C}^{2}=C{D}^{2}+A{D}^{2}-2CD\cdot AD \cos \mathrm{\angle }ADC $ ,

即 $ 189={x}^{2}+{12}^{2}-2x\cdot 12×(-\dfrac{1}{2}) $ ,

整理得 $ {x}^{2}+12x-45=0 $ ,解得 $ x=3 $ 或 $ x=-15 $ （舍）,即 $ CD=3 $ .

（3）在 $ △ABC $ 中, $ AB=12 $ ,由正弦定理 $ \dfrac{AB}{ \sin C}=\dfrac{BC}{ \sin A} $ 得, $ BC=\dfrac{12 \sin A}{ \sin C}=\dfrac{12 \sin (\dfrac{2\mathrm{\pi }}{3}-C)}{ \sin C}=\dfrac{12(\dfrac{\sqrt{3}}{2} \cos C+\dfrac{1}{2} \sin C)}{ \sin C}=12(\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\cdot \dfrac{1}{ \tan C}) $ ,

$ \therefore {S}_{△ABC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot \sin B=36\sqrt{3}\cdot (\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\cdot \dfrac{1}{ \tan C}) $ .

$ \because △ABC $ 是锐角三角形, $ \therefore 0 < C < \dfrac{\mathrm{\pi }}{2} $ ,且 $ 0 < \dfrac{2\mathrm{\pi }}{3}-C < \dfrac{\mathrm{\pi }}{2} $ ,

$ \therefore \dfrac{\mathrm{\pi }}{6} < C < \dfrac{\mathrm{\pi }}{2} $ ,则 $ \tan C > \dfrac{\sqrt{3}}{3} $ ,即 $ 0 < \dfrac{1}{ \tan C} < \sqrt{3} $ , $ \dfrac{1}{2} < \dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\cdot \dfrac{1}{ \tan C} < 2 $ ,

$ \therefore 18\sqrt{3} < {S}_{△ABC} < 72\sqrt{3} $ ,

$ \therefore △ABC $ 面积的取值范围是 $ (18\sqrt{3},72\sqrt{3}) $ .

解析：

12．已知 $ a $ , $ b $ , $ c $ 分别为 $ △ABC $ 三个内角 $ A $ , $ B $ , $ C $ 的对边，且 $ (c+a)\cdot ( \sin C- \sin A)=(c-b) \sin B $ .

（1）求 $ A $ ；

（2）在 $ △ABC $ 中，若 $ BC $ 边的中线 $ AD=1 $ ，求 $ △ABC $ 面积的最大值.

答案：

（1）【解】由正弦定理,得 $ (c+a)(c-a)=(c-b)b $ ,即 $ {b}^{2}+{c}^{2}-{a}^{2}=bc $ ,

由余弦定理,得 $ \cos A=\dfrac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}=\dfrac{1}{2} $ ,又 $ A\in (0,\mathrm{\pi }) $ ,所以 $ A=\dfrac{\mathrm{\pi }}{3} $ .

（2）因为 $ D $ 是 $ BC $ 边的中点,所以 $ \cos \mathrm{\angle }ADC=\dfrac{C{D}^{2}+A{D}^{2}-A{C}^{2}}{2CD\cdot AD}=\dfrac{\dfrac{{a}^{2}}{4}+{1}^{2}-{b}^{2}}{2\cdot \dfrac{a}{2}\cdot 1} $ , $ \cos \mathrm{\angle }ADB=\dfrac{D{B}^{2}+A{D}^{2}-A{B}^{2}}{2DB\cdot AD}=\dfrac{\dfrac{{a}^{2}}{4}+{1}^{2}-{c}^{2}}{2\cdot \dfrac{a}{2}\cdot 1} $ .

因为 $ \mathrm{\angle }ADC+\mathrm{\angle }ADB=\mathrm{\pi } $ ,所以 $ \dfrac{\dfrac{{a}^{2}}{4}+{1}^{2}-{b}^{2}}{a}+\dfrac{\dfrac{{a}^{2}}{4}+{1}^{2}-{c}^{2}}{a}=0 $ ,所以 $ \dfrac{{a}^{2}}{2}+2={b}^{2}+{c}^{2} $ ①.

由（1）知 $ {b}^{2}+{c}^{2}-{a}^{2}=bc $ ②,

把①式代入②式,得 $ 4-bc={b}^{2}+{c}^{2} $ ,则

$ 4-bc={b}^{2}+{c}^{2}\geqslant 2bc $ ,即 $ bc\leqslant \dfrac{4}{3}( $ 当且仅当 $ b=c=\dfrac{2\sqrt{3}}{3} $ 时取等号 $ ) $ .

所以 $ {S}_{△ABC}=\dfrac{1}{2}bc \sin \mathrm{\angle }BAC=\dfrac{\sqrt{3}}{4}bc\leqslant \dfrac{\sqrt{3}}{4}×\dfrac{4}{3}=\dfrac{\sqrt{3}}{3} $ ,所以当 $ b=c=\dfrac{2\sqrt{3}}{3} $ 时, $ {S}_{△ABC} $ 取得最大值,最大值为 $ \dfrac{\sqrt{3}}{3} $ .

解析：

13．如图，在 $ △ABC $ 中， $ C=\dfrac{\mathrm{\pi }}{6} $ ， $ BC=6 $ , $ BD $ 是 $ \mathrm{\angle }ABC $ 的平分线，且 $ CD=2\sqrt{3} $ .

试题资源网 https://stzy.com

（1）求 $ BD $ ；

（2）若 $ M $ , $ N $ 是线段 $ BD $ 上的动点（点 $ N $ 在线段 $ BM $ 上），且 $ \mathrm{\angle }MAN=\dfrac{\mathrm{\pi }}{3} $ ，记 $ \mathrm{\angle }DAM $ 为 $ \theta $ .

$ {\rm （i）} $ 用 $ \tan \theta $ 表示 $ DM $ ；

（ⅱ）求 $ △MAN $ 面积的最小值.

答案：

（1）【解】在 $ △BCD $ 中,由余弦定理,得

$ B{D}^{2}=C{B}^{2}+C{D}^{2}-2CB\cdot CD \cos C={6}^{2}+{\left(2\sqrt{3}\right) ^ {2}}-2×6×2\sqrt{3}×\dfrac{\sqrt{3}}{2}=12 $ ,

所以 $ BD=2\sqrt{3} $ .

（2） $ {\rm （i）} $ 由（1）可知 $ \mathrm{\angle }DBC=\mathrm{\angle }ABD=C=\dfrac{\mathrm{\pi }}{6} $ ,

所以 $ \mathrm{\angle }ABC=\dfrac{\mathrm{\pi }}{3} $ , $ \mathrm{\angle }BAC=\dfrac{\mathrm{\pi }}{2} $ ,故 $ AD=\dfrac{1}{2}BD=\sqrt{3} $ , $ AB=\dfrac{1}{2}BC=3 $ , $ \mathrm{\angle }ADB=\dfrac{\mathrm{\pi }}{3} $ .

因为 $ \mathrm{\angle }DAM=\theta $ ,所以 $ \mathrm{\angle }AMD=\dfrac{2\mathrm{\pi }}{3}-\theta $ .

在 $ △ADM $ 中,由正弦定理得, $ \dfrac{DM}{ \sin \mathrm{\angle }DAM}=\dfrac{AD}{ \sin \mathrm{\angle }AMD} $ ,即 $ \dfrac{DM}{ \sin \theta }=\dfrac{\sqrt{3}}{ \sin (\dfrac{2\mathrm{\pi }}{3}-\theta )} $ ,

易知 $ \cos \theta \ne 0 $ ,所以 $ DM=\dfrac{\sqrt{3} \sin \theta }{ \sin (\dfrac{2\mathrm{\pi }}{3}-\theta )}=\dfrac{\sqrt{3} \sin \theta }{\dfrac{\sqrt{3}}{2} \cos \theta +\dfrac{1}{2} \sin \theta }=\dfrac{2\sqrt{3} \tan \theta }{ \tan \theta +\sqrt{3}} $ , $ \theta \in [0,\dfrac{\mathrm{\pi }}{6}] $ .

（ⅱ）因为 $ \mathrm{\angle }BAC=\dfrac{\mathrm{\pi }}{2} $ , $ \mathrm{\angle }MAN=\dfrac{\mathrm{\pi }}{3} $ , $ \mathrm{\angle }DAM=\theta $ ,所以 $ \mathrm{\angle }BAN=\dfrac{\mathrm{\pi }}{6}-\theta $ ,

又 $ \mathrm{\angle }ABD=\dfrac{\mathrm{\pi }}{6} $ ,所以 $ \mathrm{\angle }ANB=\dfrac{2\mathrm{\pi }}{3}+\theta $ .

在 $ △ABN $ 中,由正弦定理得, $ \dfrac{BN}{ \sin \mathrm{\angle }BAN}=\dfrac{AB}{ \sin \mathrm{\angle }ANB} $ ,即 $ \dfrac{BN}{ \sin (\dfrac{\mathrm{\pi }}{6}-\theta )}=\dfrac{3}{ \sin (\dfrac{2\mathrm{\pi }}{3}+\theta )} $ ,

所以 $ BN=\dfrac{3 \sin (\dfrac{\mathrm{\pi }}{6}-\theta )}{ \sin (\dfrac{2\mathrm{\pi }}{3}+\theta )}= $

$ \dfrac{\dfrac{3}{2} \cos \theta -\dfrac{3\sqrt{3}}{2} \sin \theta }{\dfrac{\sqrt{3}}{2} \cos \theta -\dfrac{1}{2} \sin \theta }=\dfrac{3-3\sqrt{3} \tan \theta }{\sqrt{3}- \tan \theta } $ .

设点 $ A $ 到 $ BD $ 的距离为 $ d $ ,则 $ d=\dfrac{AB\cdot AD}{BD}=\dfrac{3×\sqrt{3}}{2\sqrt{3}}=\dfrac{3}{2} $ ,

所以 $ {S}_{△MAN}=\dfrac{1}{2}MN\cdot d=\dfrac{3}{4}(BD-DM-BN)=\dfrac{3}{4}(2\sqrt{3}-DM-BN) $ ,

要求 $ △MAN $ 面积的最小值,即求 $ DM+BN $ 的最大值.

由题意得, $ DM+BN=\dfrac{2\sqrt{3} \tan \theta }{ \tan \theta +\sqrt{3}}+\dfrac{3-3\sqrt{3} \tan \theta }{\sqrt{3}- \tan \theta }=5\sqrt{3}-\dfrac{12\sqrt{3}}{3-{ \tan }^{2}\theta } $ .

因为 $ \theta \in [0,\dfrac{\mathrm{\pi }}{6}] $ ,所以 $ 3-{ \tan }^{2}\theta \in [\dfrac{8}{3},3]⇒\dfrac{12\sqrt{3}}{3-{ \tan }^{2}\theta }\in [4\sqrt{3},\dfrac{9\sqrt{3}}{2}]⇒5\sqrt{3}-\dfrac{12\sqrt{3}}{3-{ \tan }^{2}\theta }\in [\dfrac{\sqrt{3}}{2},\sqrt{3}] $ ,

故 $ DM+BN $ 的最大值为 $ \sqrt{3} $ ,

所以 $ △MAN $ 面积的最小值为 $ \dfrac{3}{4}×(2\sqrt{3}-\sqrt{3})=\dfrac{3\sqrt{3}}{4} $ .

解析：

专题4 解三角形中的最值及范围问题

一、刷难关