第6.3节综合训练

一、刷能力

1．已知向量 $ \boldsymbol{a}=(2,-2) $ ， $ \boldsymbol{b}=(-1,2) $ ，若 $ \boldsymbol{c}=(x,y) $ ，且满足 $ (\boldsymbol{a}-\boldsymbol{c})\perp \boldsymbol{b} $ ，则 $ x-2y= $ （      ）

A．2

B．4

C．5

D．6

答案：D
解析：

因为 $ \boldsymbol{a}=(2,-2) $ , $ \boldsymbol{c}=(x,y) $ ,所以 $ \boldsymbol{a}-\boldsymbol{c}=(2-x,-2-y) $ .又 $ (\boldsymbol{a}-\boldsymbol{c})\perp \boldsymbol{b} $ ,则 $ (2-x)×(-1)+(-2-y)×2=0 $ ,化简得 $ x-2y=6 $ .故选 $ \mathrm{D} $ .

2．已知 $ \overrightarrow {AC}=(-1,3) $ ， $ \overrightarrow {AB}=(3,1) $ ，若线段 $ BC $ 的一个三等分点为 $ M $ ，则 $ \overrightarrow {AM} $ 的坐标为（      ）

A． $ (\dfrac{5}{3},\dfrac{5}{3}) $

B． $ (\dfrac{1}{3},\dfrac{7}{3}) $ 或 $ (\dfrac{5}{3},\dfrac{5}{3}) $

C． $ (\dfrac{7}{3},\dfrac{1}{3}) $

D． $ (\dfrac{7}{3},\dfrac{1}{3}) $ 或 $ (\dfrac{10}{3},\dfrac{7}{3}) $

答案：B
解析：

由线段 $ BC $ 的一个三等分点为 $ M $ ,得 $ 2\overrightarrow {CM}=\overrightarrow {MB} $ 或 $ \overrightarrow {CM}=2\overrightarrow {MB} $ ,

若 $ 2\overrightarrow {CM}=\overrightarrow {MB} $ ,则 $ 2\overrightarrow {AM}-2\overrightarrow {AC}=\overrightarrow {AB}-\overrightarrow {AM} $ ,则 $ \overrightarrow {AM}=\dfrac{1}{3}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AC}=(\dfrac{1}{3},\dfrac{7}{3}) $ ；

若 $ \overrightarrow {CM}=2\overrightarrow {MB} $ ,则 $ \overrightarrow {AM}-\overrightarrow {AC}=2\overrightarrow {AB}-2\overrightarrow {AM} $ ,则 $ \overrightarrow {AM}=\dfrac{2}{3}\overrightarrow {AB}+\dfrac{1}{3}\overrightarrow {AC}=(\dfrac{5}{3},\dfrac{5}{3}) $ .

故选 $ \mathrm{B} $ .

3．在 $ △ABC $ 中， $ N $ 是 $ AC $ 边上一点，且 $ \overrightarrow {AN}=\dfrac{1}{2}\overrightarrow {NC} $ ， $ P $ 是 $ BN $ 上一点.若 $ \overrightarrow {AP}=m\overrightarrow {AB}+\dfrac{2}{9}\overrightarrow {AC} $ ，则实数 $ m= $ （      ）

A． $ \dfrac{1}{2} $

B． $ \dfrac{1}{3} $

C． $ \dfrac{1}{4} $

D．1

答案：B
解析：

如图,因为 $ \overrightarrow {AN}=\dfrac{1}{2}\overrightarrow {NC} $ ,所以 $ \overrightarrow {AC}=3\overrightarrow {AN} $ ,则 $ \overrightarrow {AP}=m\overrightarrow {AB}+\dfrac{2}{9}\overrightarrow {AC}=m\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AN} $ .又因为 $ B $ , $ P $ , $ N $ 三点共线,所以 $ m+\dfrac{2}{3}=1 $ ,故 $ m=\dfrac{1}{3} $ .

试题资源网 https://stzy.com

4．（多选）在 $ △ABC $ 中，已知 $ \mathrm{\angle }BAC=\dfrac{\mathrm{\pi }}{2} $ , $ AB=AC $ , $ D $ 是 $ AC $ 的中点，若 $ P $ 是 $ BC $ 上的一点，且满足 $ \overrightarrow {BP}=2\overrightarrow {PC} $ , $ AP $ 与 $ BD $ 交于点 $ E $ ，则（      ）（多选）

A． $ \overrightarrow {AP}=\dfrac{1}{3}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AC} $

B． $ \overrightarrow {AP} $ 在 $ \overrightarrow {AB} $ 上的投影向量为 $ \dfrac{2}{3}\overrightarrow {AB} $

C． $ \overrightarrow {AP}\cdot \overrightarrow {BD}=0 $

D． $ \overrightarrow {AE}=\dfrac{3}{5}\overrightarrow {AP} $

答案：ACD
解析：

对于 $ \mathrm{A} $ , $ \because \overrightarrow {BP}=2\overrightarrow {PC} $ ,

$ \therefore \overrightarrow {BP}=\dfrac{2}{3}\overrightarrow {BC} $ , $ \therefore \overrightarrow {AP}=\overrightarrow {AB}+\overrightarrow {BP}=\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {BC}=\overrightarrow {AB}+\dfrac{2}{3}(\overrightarrow {AC}-\overrightarrow {AB})=\dfrac{1}{3}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AC} $ ,故 $ \mathrm{A} $ 正确；

对于 $ \mathrm{B} $ , $ \because \mathrm{\angle }BAC=\dfrac{\mathrm{\pi }}{2} $ ,且 $ \overrightarrow {AP}=\dfrac{1}{3}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AC} $ , $ \therefore \overrightarrow {AP} $ 在 $ \overrightarrow {AB} $ 上的投影向量为 $ \dfrac{\overrightarrow {AP}\cdot \overrightarrow {AB}}{|\overrightarrow {AB}{|}^{2}}\cdot \overrightarrow {AB}=\dfrac{\dfrac{1}{3}|\overrightarrow {AB}{|}^{2}}{|\overrightarrow {AB}{|}^{2}}\cdot \overrightarrow {AB}=\dfrac{1}{3}\overrightarrow {AB} $ ,故 $ \mathrm{B} $ 错误；

对于 $ \mathrm{C} $ , $ \because D $ 是 $ AC $ 的中点, $ \therefore \overrightarrow {BD}=\overrightarrow {AD}-\overrightarrow {AB}=\dfrac{1}{2}\overrightarrow {AC}-\overrightarrow {AB} $ ,

则 $ \overrightarrow {AP}\cdot \overrightarrow {BD}=(\dfrac{1}{3}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AC})\cdot (\dfrac{1}{2}\overrightarrow {AC}-\overrightarrow {AB})=-\dfrac{1}{3}{\overrightarrow {AB}}^{2}+\dfrac{1}{3}{\overrightarrow {AC}}^{2}-\dfrac{1}{2}\overrightarrow {AB}\cdot \overrightarrow {AC} $ ,又 $ \mathrm{\angle }BAC=\dfrac{\mathrm{\pi }}{2} $ , $ AB=AC $ , $ \therefore |\overrightarrow {AB}|=|\overrightarrow {AC}| $ , $ \overrightarrow {AB}\cdot \overrightarrow {AC}=0 $ ,即 $ \overrightarrow {AP}\cdot \overrightarrow {BD}=-\dfrac{1}{3}{\overrightarrow {AB}}^{2}+\dfrac{1}{3}{\overrightarrow {AC}}^{2}-\dfrac{1}{2}\overrightarrow {AB}\cdot \overrightarrow {AC}=0 $ ,故 $ \mathrm{C} $ 正确；

对于 $ \mathrm{D} $ ,设 $ \overrightarrow {AE}=\lambda \overrightarrow {AP}=\dfrac{1}{3}\lambda \overrightarrow {AB}+\dfrac{2}{3}\lambda \overrightarrow {AC}(0 < \lambda < 1) $ , $ \because B $ , $ E $ , $ D $ 三点共线, $ \therefore $ 设 $ \overrightarrow {AE}=\mu \overrightarrow {AB}+(1-\mu )\overrightarrow {AD}=\mu \overrightarrow {AB}+\dfrac{1-\mu }{2}\overrightarrow {AC} $ ,则 $ \begin{cases}\dfrac{1}{3}\lambda =\mu ,\\ \dfrac{2}{3}\lambda =\dfrac{1-\mu }{2},\end{cases} $ 解得 $ \begin{cases}\lambda =\dfrac{3}{5},\\ \mu =\dfrac{1}{5},\end{cases}\therefore \overrightarrow {AE}=\dfrac{3}{5}\overrightarrow {AP} $ ,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{A}\mathrm{C}\mathrm{D} $ .

试题资源网 https://stzy.com

5．已知 $ △ABC $ 中， $ |\overrightarrow {AB}|=6 $ ， $ |\overrightarrow {AC}|=6 $ ，且 $ |\lambda \overrightarrow {AB}+(1-\lambda )\overrightarrow {AC}|(\lambda \in \boldsymbol{R}) $ 的最小值为 $ 3\sqrt{2} $ ，若 $ P $ 为边 $ AB $ 上任意一点，则 $ \overrightarrow {PB}\cdot \overrightarrow {PC} $ 的最小值是（      ）

A． $ -12 $

B． $ -11 $

C． $ -10 $

D． $ -9 $

答案：D
解析：

设 $ \overrightarrow {AD}=\lambda \overrightarrow {AB}+(1-\lambda )\overrightarrow {AC} $ ,则 $ \overrightarrow {AD}-\overrightarrow {AC}=\lambda \overrightarrow {AB}-\lambda \overrightarrow {AC} $ ,得 $ \overrightarrow {CD}=\lambda \overrightarrow {CB} $ ,又 $ \overrightarrow {CD} $ 与 $ \overrightarrow {CB} $ 有共同端点 $ C $ ,所以 $ B $ , $ C $ , $ D $ 三点共线,

由 $ |\lambda \overrightarrow {AB}+(1-\lambda )\overrightarrow {AC}| $ 的最小值为 $ 3\sqrt{2} $ 可知, $ △ABC $ 的高 $ AD $ 为 $ 3\sqrt{2} $ ,如图所示,

试题资源网 https://stzy.com

因为 $ |\overrightarrow {AC}|=|\overrightarrow {AB}|=6 $ ,所以 $ △ABC $ 为等腰三角形.

在 $ \mathrm{R}\mathrm{t}△ADC $ 中, $ A{D}^{2}+{\left(\dfrac{1}{2}BC\right) ^ {2}}=A{C}^{2} $ ,即 $ (3\sqrt{2})^{2}+\dfrac{1}{4}B{C}^{2}={6}^{2} $ ,解得 $ BC=6\sqrt{2} $ ,

在 $ △ABC $ 中, $ A{B}^{2}+A{C}^{2}=B{C}^{2} $ ,所以 $ △ABC $ 是以 $ \mathrm{\angle }BAC $ 为直角的等腰直角三角形.

以点 $ A $ 为坐标原点, $ AB $ , $ AC $ 所在直线分别为 $ x $ , $ y $ 轴建立如图所示的平面直角坐标系,

试题资源网 https://stzy.com

设点 $ P(x,0) $ ,其中 $ 0\leqslant x\leqslant 6 $ ,且 $ B(6,0) $ , $ C(0,6) $ ,则 $ \overrightarrow {PB}=(6-x,0) $ , $ \overrightarrow {PC}=(-x,6) $ ,所以 $ \overrightarrow {PB}\cdot \overrightarrow {PC}=-x(6-x)={x}^{2}-6x={\left(x-3\right) ^ {2}}-9\geqslant -9 $ ,当且仅当 $ x=3 $ 时,等号成立,即 $ \overrightarrow {PB}\cdot \overrightarrow {PC} $ 取最小值 $ -9 $ .故选 $ \mathrm{D} $ .

6．（多选）已知点 $ P $ 是 $ △ABC $ 所在平面内一点，且 $ \overrightarrow {AP}=2m\overrightarrow {AB}+n\overrightarrow {AC} $ , $ m $ , $ n\in \boldsymbol{R} $ ，则下列说法正确的是（      ）（多选）

A．若 $ m=n=\dfrac{1}{2} $ ，则点 $ P $ 是边 $ BC $ 的中点

B．若点 $ P $ 是边 $ BC $ 上靠近 $ B $ 点的三等分点，则 $ m=n=\dfrac{1}{3} $

C．若 $ 2m+n=\dfrac{1}{2} $ ，则 $ {S}_{△PBC}=2{S}_{△ABC} $

D．若点 $ P $ 在 $ BC $ 边的中线上，且 $ 2m+n=\dfrac{2}{3} $ ，则点 $ P $ 是 $ △ABC $ 的重心

答案：BD
解析：

对于 $ \mathrm{A} $ ,若 $ P $ 为边 $ BC $ 的中点,则 $ \overrightarrow {AP}=\dfrac{1}{2}\overrightarrow {AB}+\dfrac{1}{2}\overrightarrow {AC} $ ,又 $ \overrightarrow {AP}=2m\overrightarrow {AB}+n\overrightarrow {AC} $ ,则 $ m=\dfrac{1}{4} $ , $ n=\dfrac{1}{2} $ ,故 $ \mathrm{A} $ 错误；

对于 $ \mathrm{B} $ ,若点 $ P $ 是边 $ BC $ 上靠近点 $ B $ 的三等分点,则 $ \overrightarrow {AP}=\overrightarrow {AB}+\overrightarrow {BP}=\overrightarrow {AB}+\dfrac{1}{3}\overrightarrow {BC}=\overrightarrow {AB}+\dfrac{1}{3}(\overrightarrow {AC}-\overrightarrow {AB})=\dfrac{2}{3}\overrightarrow {AB}+\dfrac{1}{3}\overrightarrow {AC} $ ,

又 $ \overrightarrow {AP}=2m\overrightarrow {AB}+n\overrightarrow {AC} $ ,则 $ 2m=\dfrac{2}{3} $ , $ n=\dfrac{1}{3} $ ,即 $ m=n=\dfrac{1}{3} $ ,故 $ \mathrm{B} $ 正确；

对于 $ \mathrm{C} $ ,若 $ 2m+n=\dfrac{1}{2} $ ,则 $ 2\overrightarrow {AP}=2(2m\overrightarrow {AB}+n\overrightarrow {AC})=4m\overrightarrow {AB}+2n\overrightarrow {AC} $ ,且 $ 4m+2n=1 $ ,

设 $ \overrightarrow {AM}=2\overrightarrow {AP} $ ,即 $ \overrightarrow {AM}=4m\overrightarrow {AB}+2n\overrightarrow {AC} $ ,则点 $ M $ 在 $ BC $ 边上,

因为点 $ P $ 为 $ AM $ 的中点,所以 $ {S}_{△PBC}=\dfrac{1}{2}{S}_{△ABC} $ ,故 $ \mathrm{C} $ 错误；

对于 $ \mathrm{D} $ ,若 $ 2m+n=\dfrac{2}{3} $ ,所以 $ \dfrac{3}{2}\overrightarrow {AP}=\dfrac{3}{2}\cdot (2m\overrightarrow {AB}+n\overrightarrow {AC})=3m\overrightarrow {AB}+\dfrac{3}{2}n\overrightarrow {AC} $ ,且 $ 3m+\dfrac{3}{2}n=1 $ ,

设 $ \overrightarrow {AN}=\dfrac{3}{2}\overrightarrow {AP} $ ,即 $ \overrightarrow {AN}=3m\overrightarrow {AB}+\dfrac{3}{2}n\overrightarrow {AC} $ ,则点 $ N $ 在 $ BC $ 上,又因为 $ P $ 在 $ BC $ 边的中线上,所以 $ AN $ 为中线,所以点 $ P $ 为 $ △ABC $ 的重心,故 $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{D} $ .

7．若 $ \boldsymbol{a}=(\lambda ,4) $ ， $ \boldsymbol{b}=(-3,5) $ ，且 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 的夹角为钝角，则 $ \lambda $ 的取值范围是            .

答案：

$ (\dfrac{20}{3},+\mathrm{\infty }) $

解析：

设 $ \theta $ 为 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 的夹角,则 $ \cos \theta =\dfrac{\boldsymbol{a}\cdot \boldsymbol{b}}{|\boldsymbol{a}||\boldsymbol{b}|}=\dfrac{-3\lambda +20}{\sqrt{{\lambda }^{2}+16}\cdot \sqrt{34}} $ ,

因为 $ \theta $ 为钝角,所以 $ -3\lambda +20 < 0 $ ,解得 $ \lambda > \dfrac{20}{3} $ .

因为 $ \boldsymbol{a} $ 与 $ \boldsymbol{b} $ 不平行,所以 $ 5\lambda +12\ne 0 $ ,解得 $ \lambda \ne -\dfrac{12}{5} $ ,

综上可得, $ \lambda $ 的取值范围是 $ (\dfrac{20}{3},+\mathrm{\infty }) $ .

8．如图所示， $ A $ ， $ B $ ， $ C $ 是圆 $ O $ 上的三点， $ CO $ 的延长线与 $ BA $ 的延长线交于圆 $ O $ 外一点 $ D $ .若 $ \overrightarrow {OC}=m\overrightarrow {OA}+n\overrightarrow {OB} $ ，则 $ m+n $ 的取值范围是        .

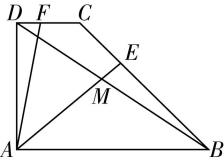
试题资源网 https://stzy.com

答案：

$ (-1,0) $

解析：

由 $ D $ 是圆 $ O $ 外一点,可设 $ \overrightarrow {BD}=\lambda \overrightarrow {BA}(\lambda > 1) $ ,则 $ \overrightarrow {OD}=\overrightarrow {OB}+\lambda \overrightarrow {BA}=\lambda \overrightarrow {OA}+(1-\lambda )\overrightarrow {OB} $ .又因为 $ C $ , $ O $ , $ D $ 三点共线,所以令 $ \overrightarrow {OD}=-\mu \overrightarrow {OC}(\mu > 1) $ ,则 $ \overrightarrow {OC}=-\dfrac{\lambda }{\mu }\overrightarrow {OA}-\dfrac{1-\lambda }{\mu }\overrightarrow {OB}(\lambda > 1,\mu > 1) $ ,所以 $ m=-\dfrac{\lambda }{\mu } $ , $ n=-\dfrac{1-\lambda }{\mu } $ ,则 $ m+n=-\dfrac{\lambda }{\mu }-\dfrac{1-\lambda }{\mu }=-\dfrac{1}{\mu }\in (-1,0) $ .

9．已知 $ |\boldsymbol{u}|=3 $ ， $ |\boldsymbol{v}|=4 $ ，且 $ \boldsymbol{u}\cdot \boldsymbol{v}=0 $ .若 $ |\boldsymbol{a}|=1 $ ，则当 $ t\in [0,1] $ 时， $ |\boldsymbol{a}-t\boldsymbol{u}-(1-t)\boldsymbol{v}| $ 的取值范围为        .

答案：

$ [\dfrac{7}{5},5] $

解析：

因为 $ \boldsymbol{u}\cdot \boldsymbol{v}=0 $ ,所以 $ \boldsymbol{u}\perp \boldsymbol{v} $ ,故可以建立平面直角坐标系,如图所示.又 $ |\boldsymbol{u}|=3 $ , $ |\boldsymbol{v}|=4 $ ,

设 $ C(3,0) $ , $ D(0,4) $ ,则可令 $ \overrightarrow {OC}=\boldsymbol{u} $ , $ \overrightarrow {OD}=\boldsymbol{v} $ ,在线段 $ CD $ 上取点 $ B $ ,

因为 $ B $ , $ C $ , $ D $ 三点共线,所以存在 $ t\in [0,1] $ ,使得 $ \overrightarrow {OB}=t\overrightarrow {OC}+(1-t)\overrightarrow {OD}=t\boldsymbol{u}+(1-t)\boldsymbol{v} $ ,

试题资源网 https://stzy.com

又 $ |\boldsymbol{a}|=1 $ ,取 $ \overrightarrow {OA}=\boldsymbol{a} $ ,则点 $ A $ 在以点 $ O $ 为圆心,1为半径的圆上,

则 $ |\boldsymbol{a}-t\boldsymbol{u}-(1-t)\boldsymbol{v}|=|\overrightarrow {OA}-\overrightarrow {OB}|=|\overrightarrow {AB}| $ .

因为 $ \mathrm{R}\mathrm{t}△OCD $ 的斜边 $ CD $ 上的高为 $ \dfrac{3×4}{5}=\dfrac{12}{5} $ ,

所以当 $ OB\perp CD $ , $ A $ 为 $ OB $ 与圆 $ O $ 的交点且 $ A $ 在 $ O $ , $ B $ 之间时, $ |\overrightarrow {AB}| $ 取得最小值,为 $ \dfrac{12}{5}-1=\dfrac{7}{5} $ ；

当点 $ B $ 与点 $ D $ 重合,点 $ A $ 坐标为 $ (0,-1) $ 时, $ |\overrightarrow {AB}| $ 取得最大值,为 $ 4+1=5 $ .

所以 $ \dfrac{7}{5}\leqslant |\overrightarrow {AB}|\leqslant 5 $ .故 $ |\boldsymbol{a}-t\boldsymbol{u}-(1-t)\boldsymbol{v}| $ 的取值范围为 $ [\dfrac{7}{5},5] $ .

10．如图，已知 $ O $ 为平面直角坐标系的原点， $ \mathrm{\angle }OAB={120}^{\circ } $ ， $ BC//y $ 轴， $ |\overrightarrow {OA}|=2|\overrightarrow {AB}|=4 $ ， $ \overrightarrow {OB}\cdot \overrightarrow {OC}=40 $ .

试题资源网 https://stzy.com

（1） 求点 $ B $ ， $ C $ 的坐标；

（2） 求向量 $ \overrightarrow {BC} $ 在向量 $ \overrightarrow {OC} $ 上的投影向量的坐标.

答案：

（1） 【解】由条件可知, $ \mathrm{\angle }BAx={60}^{\circ } $ ,所以点 $ B $ 的横坐标 $ {x}_{B}=4+2 \cos {60}^{\circ }=5 $ ,纵坐标 $ {y}_{B}=2 \sin {60}^{\circ }=\sqrt{3} $ ,即 $ B(5,\sqrt{3}) $ .

由条件可知, $ {x}_{C}={x}_{B}=5 $ ,则设 $ C(5,y) $ ,

所以 $ \overrightarrow {OB}\cdot \overrightarrow {OC}=25+\sqrt{3}y=40 $ ,则 $ y=5\sqrt{3} $ ,即 $ C(5,5\sqrt{3}) $ ,所以 $ B(5,\sqrt{3}) $ , $ C(5,5\sqrt{3}) $ .

（2） 由（1）可知, $ \overrightarrow {BC}=(0,4\sqrt{3}) $ , $ \overrightarrow {OC}=(5,5\sqrt{3}) $ ,

所以向量 $ \overrightarrow {BC} $ 在向量 $ \overrightarrow {OC} $ 上的投影向量为 $ \dfrac{\overrightarrow {BC}\cdot \overrightarrow {OC}}{{|\overrightarrow {OC}|}^{2}}\cdot \overrightarrow {OC}=\dfrac{60}{100}(5,5\sqrt{3})=(3,3\sqrt{3}) $ ,

所以向量 $ \overrightarrow {BC} $ 在向量 $ \overrightarrow {OC} $ 上的投影向量的坐标为 $ (3,3\sqrt{3}) $ .

解析：

11．已知平面向量 $ \boldsymbol{a}=(2,1) $ , $ \boldsymbol{b}=(m-2,4-2m) $ , $ \boldsymbol{c}=\boldsymbol{a}+\boldsymbol{b} $ .

（1） 若 $ \boldsymbol{a}//\boldsymbol{b} $ ，求实数 $ m $ 的值；

（2） 证明：对任意的 $ \lambda \ne 0 $ ，都有 $ \boldsymbol{a}\perp \lambda (\boldsymbol{a}-\boldsymbol{c}) $ ；

（3） 若 $ \boldsymbol{a} $ 与 $ \boldsymbol{c} $ 的夹角为 $ \dfrac{\mathrm{\pi }}{4} $ ，求 $ |\boldsymbol{c}| $ 的值.

答案：

（1） 【解】因为平面向量 $ \boldsymbol{a}=(2,1) $ , $ \boldsymbol{b}=(m-2,4-2m) $ , $ \boldsymbol{a}//\boldsymbol{b} $ ,

所以 $ 2(4-2m)=m-2 $ ,解得 $ m=2 $ .

（2） 【证明】因为 $ \boldsymbol{c}=\boldsymbol{a}+\boldsymbol{b} $ , $ \boldsymbol{a}=(2,1) $ ,所以 $ \boldsymbol{a}-\boldsymbol{c}=-\boldsymbol{b}=(2-m,2m-4) $ ,

所以 $ \boldsymbol{a}\cdot \lambda (\boldsymbol{a}-\boldsymbol{c})=\lambda \boldsymbol{a}\cdot (\boldsymbol{a}-\boldsymbol{c})=\lambda [2×(2-m)+1×(2m-4)]=\lambda (4-2m+2m-4)=0 $ ,

所以对任意的 $ \lambda \ne 0 $ ,都有 $ \boldsymbol{a}\perp \lambda (\boldsymbol{a}-\boldsymbol{c}) $ .

（3） 【解】由题知 $ \boldsymbol{c}=\boldsymbol{a}+\boldsymbol{b}=(2,1)+(m-2,4-2m)=(m,5-2m) $ ,

因为 $ \boldsymbol{a} $ 与 $ \boldsymbol{c} $ 的夹角为 $ \dfrac{\mathrm{\pi }}{4} $ ,

所以 $ \cos \dfrac{\mathrm{\pi }}{4}=\dfrac{\boldsymbol{a}\cdot \boldsymbol{c}}{|\boldsymbol{a}||\boldsymbol{c}|}=\dfrac{2m+5-2m}{\sqrt{{2}^{2}+{1}^{2}}×|\boldsymbol{c}|}=\dfrac{5}{\sqrt{{2}^{2}+{1}^{2}}×|\boldsymbol{c}|}=\dfrac{\sqrt{2}}{2} $ ,则 $ |\boldsymbol{c}|=\sqrt{10} $ .

解析：

12．在平面直角坐标系 $ xOy $ 中，已知点 $ A(3,3) $ , $ B(5,1) $ , $ P(2,1) $ .

（1） 求 $ |\overrightarrow {PA}-\overrightarrow {PB}| $ 的值；

（2） 设点 $ M $ 是坐标平面内一点，且四边形 $ APBM $ 是平行四边形，求点 $ M $ 的坐标；

（3） 若点 $ N $ 是直线 $ OP $ 上的动点，求 $ \overrightarrow {NA}\cdot \overrightarrow {NB} $ 的最小值.

答案：

（1） 【解】由题意可知 $ \overrightarrow {PA}=(1,2) $ , $ \overrightarrow {PB}=(3,0) $ , $ \therefore \overrightarrow {PA}-\overrightarrow {PB}=(-2,2) $ , $ \therefore |\overrightarrow {PA}-\overrightarrow {PB}|=\sqrt{{\left(-2\right) ^ {2}}+{2}^{2}}=2\sqrt{2} $ .

（2） 如图①所示, $ \because $ 四边形 $ APBM $ 是平行四边形,故有 $ \overrightarrow {PA}=\overrightarrow {BM} $ ,设 $ M(x,y) $ ,

试题资源网 https://stzy.com

图①

则 $ \overrightarrow {PA}=(1,2)=\overrightarrow {BM}=(x-5,y-1) $ ,解得 $ x=6 $ , $ y=3 $ , $ \therefore M(6,3) $ .

（3） 如图②所示,易知直线 $ OP $ 的方程为 $ y=\dfrac{1}{2}x $ ,不妨设 $ N(2a,a) $ ,则 $ \overrightarrow {NA}\cdot \overrightarrow {NB}= (3-2a,3-a )\cdot (5-2a,1-a )=5{a}^{2}-20a+18=5 (a-2)^{2}-2\geqslant -2 $ ,当且仅当 $ a=2 $ ,即 $ N(4,2) $ 时, $ \overrightarrow {NA}\cdot \overrightarrow {NB} $ 取得最小值 $ -2 $ .

试题资源网 https://stzy.com

图②

解析：

13．在直角梯形 $ ABCD $ 中，已知 $ AB//DC $ ， $ AD\perp AB $ ， $ CD=1 $ ， $ AD=2 $ ， $ AB=3 $ ，动点 $ E $ ， $ F $ 分别在线段 $ BC $ 和 $ DC $ 上， $ AE $ 和 $ BD $ 交于点 $ M $ ，且 $ \overrightarrow {BE}=\lambda \overrightarrow {BC} $ ， $ \overrightarrow {DF}=(1-\lambda )\overrightarrow {DC} $ ， $ \lambda \in [0,1]. $

试题资源网 https://stzy.com

（1） 当 $ \lambda =\dfrac{1}{2} $ 时，求 $ \overrightarrow {AE}\cdot \overrightarrow {BD} $ 的值；

（2） 当 $ \lambda =\dfrac{2}{3} $ 时，求 $ \dfrac{DM}{MB} $ 的值；

（3） 求 $ |\overrightarrow {AF}+\dfrac{1}{2}\overrightarrow {AE}| $ 的取值范围.

答案：

（1） 【解】当 $ \lambda =\dfrac{1}{2} $ 时, $ \overrightarrow {BE}=\dfrac{1}{2}\overrightarrow {BC} $ ,

因为 $ \overrightarrow {BC}=\overrightarrow {BA}+\overrightarrow {AD}+\overrightarrow {DC}=-\overrightarrow {AB}+\overrightarrow {AD}+\dfrac{1}{3}\overrightarrow {AB}=-\dfrac{2}{3}\overrightarrow {AB}+\overrightarrow {AD} $ ,

所以 $ \overrightarrow {BE}=\dfrac{1}{2}\overrightarrow {BC}=\dfrac{1}{2}(-\dfrac{2}{3}\overrightarrow {AB}+\overrightarrow {AD})=-\dfrac{1}{3}\overrightarrow {AB}+\dfrac{1}{2}\overrightarrow {AD} $ ,

所以 $ \overrightarrow {AE}=\overrightarrow {AB}+\overrightarrow {BE}=\overrightarrow {AB}-\dfrac{1}{3}\overrightarrow {AB}+\dfrac{1}{2}\overrightarrow {AD}=\dfrac{2}{3}\overrightarrow {AB}+\dfrac{1}{2}\overrightarrow {AD} $ .

又 $ \overrightarrow {BD}=\overrightarrow {AD}-\overrightarrow {AB} $ ,

所以 $ \overrightarrow {AE}\cdot \overrightarrow {BD}=(\dfrac{2}{3}\overrightarrow {AB}+\dfrac{1}{2}\overrightarrow {AD})\cdot (\overrightarrow {AD}-\overrightarrow {AB})=\dfrac{2}{3}\overrightarrow {AB}\cdot \overrightarrow {AD}+\dfrac{1}{2}{\overrightarrow {AD}}^{2}-\dfrac{2}{3}{\overrightarrow {AB}}^{2}-\dfrac{1}{2}\overrightarrow {AB}\cdot \overrightarrow {AD}=\dfrac{1}{2}×{2}^{2}-\dfrac{2}{3}×{3}^{2}=2-6=-4 $ .

（2） 当 $ \lambda =\dfrac{2}{3} $ 时, $ \overrightarrow {BE}=\dfrac{2}{3}\overrightarrow {BC} $ ,

由（1）知 $ \overrightarrow {BC}=-\dfrac{2}{3}\overrightarrow {AB}+\overrightarrow {AD} $ ,

所以 $ \overrightarrow {BE}=\dfrac{2}{3}\overrightarrow {BC}=\dfrac{2}{3}(-\dfrac{2}{3}\overrightarrow {AB}+\overrightarrow {AD})=-\dfrac{4}{9}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AD} $ ,

所以 $ \overrightarrow {AE}=\overrightarrow {AB}+\overrightarrow {BE}=\overrightarrow {AB}-\dfrac{4}{9}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AD}=\dfrac{5}{9}\overrightarrow {AB}+\dfrac{2}{3}\overrightarrow {AD} $ .

因为 $ A $ , $ M $ , $ E $ 三点共线,所以存在 $ m $ ,使 $ \overrightarrow {AM}=m\overrightarrow {AE}=\dfrac{5}{9}m\overrightarrow {AB}+\dfrac{2}{3}m\overrightarrow {AD} $ .

又因为 $ B $ , $ M $ , $ D $ 三点共线,所以 $ \dfrac{5}{9}m+\dfrac{2}{3}m=1 $ ,解得 $ m=\dfrac{9}{11} $ ,

所以 $ \overrightarrow {AM}=\dfrac{5}{11}\overrightarrow {AB}+\dfrac{6}{11}\overrightarrow {AD} $ ,所以 $ 11\overrightarrow {AM}=5\overrightarrow {AB}+6\overrightarrow {AD} $ ,所以 $ 5(\overrightarrow {AM}-\overrightarrow {AB})=6(\overrightarrow {AD}-\overrightarrow {AM}) $ ,即 $ 5\overrightarrow {BM}=6\overrightarrow {MD} $ ,所以 $ \dfrac{DM}{MB}=\dfrac{5}{6} $ .

（3） 由（1）知 $ \overrightarrow {BC}=-\dfrac{2}{3}\overrightarrow {AB}+\overrightarrow {AD} $ ,

所以 $ \overrightarrow {BE}=\lambda \overrightarrow {BC}=\lambda (-\dfrac{2}{3}\overrightarrow {AB}+\overrightarrow {AD}) $ ,

所以 $ \overrightarrow {AE}=\overrightarrow {AB}+\overrightarrow {BE}=\overrightarrow {AB}+\lambda (-\dfrac{2}{3}\overrightarrow {AB}+\overrightarrow {AD})=(1-\dfrac{2}{3}\lambda )\overrightarrow {AB}+\lambda \overrightarrow {AD} $ .

因为 $ \overrightarrow {AF}=\overrightarrow {AD}+\overrightarrow {DF}=\overrightarrow {AD}+(1-\lambda )\overrightarrow {DC}=\overrightarrow {AD}+\dfrac{1-\lambda }{3}\overrightarrow {AB} $ ,

所以 $ \overrightarrow {AF}+\dfrac{1}{2}\overrightarrow {AE}=(\dfrac{5}{6}-\dfrac{2}{3}\lambda )\overrightarrow {AB}+(1+\dfrac{\lambda }{2})\overrightarrow {AD} $ ,

所以 $ {|\overrightarrow {AF}+\dfrac{1}{2}\overrightarrow {AE}|}^{2}={\left(\dfrac{5}{6}-\dfrac{2}{3}\lambda \right) ^ {2}}{\overrightarrow {AB}}^{2}+2(\dfrac{5}{6}-\dfrac{2}{3}\lambda )(1+\dfrac{\lambda }{2})\overrightarrow {AB}\cdot \overrightarrow {AD}+{\left(1+\dfrac{\lambda }{2}\right) ^ {2}}{\overrightarrow {AD}}^{2} $ ,

$ =9{\left(\dfrac{5}{6}-\dfrac{2}{3}\lambda \right) ^ {2}}+4{\left(1+\dfrac{\lambda }{2}\right) ^ {2}}=5{\lambda }^{2}-6\lambda +\dfrac{41}{4}=5{\left(\lambda -\dfrac{3}{5}\right) ^ {2}}+\dfrac{169}{20} $ ,

由题意知 $ \lambda \in [0,1] $ ,

所以当 $ \lambda =\dfrac{3}{5} $ 时, $ |\overrightarrow {AF}+\dfrac{1}{2}\overrightarrow {AE}| $ 取得最小值 $ \dfrac{13\sqrt{5}}{10} $ ,

当 $ \lambda =0 $ 时, $ |\overrightarrow {AF}+\dfrac{1}{2}\overrightarrow {AE}| $ 取得最大值 $ \dfrac{\sqrt{41}}{2} $ ,

所以 $ |\overrightarrow {AF}+\dfrac{1}{2}\overrightarrow {AE}| $ 的取值范围是 $ [\dfrac{13\sqrt{5}}{10},\dfrac{\sqrt{41}}{2}] $ .

解析：