5.4.1 正弦函数、余弦函数的图象
一、刷基础
1.用“五点法”作 $ y=2 \sin x $ 的图象时,首先描出的五个点的横坐标是( )
A. $ {\rm 0,} \dfrac{\mathrm{\pi }}{2} $ , $ \mathrm{\pi } $ , $ \dfrac{3\mathrm{\pi }}{2} $ , $ 2\mathrm{\pi } $
B. $ {\rm 0,} \dfrac{\mathrm{\pi }}{4} $ , $ \dfrac{\mathrm{\pi }}{2} $ , $ \dfrac{3\mathrm{\pi }}{4} $ , $ \mathrm{\pi } $
C. $ {\rm 0,} \mathrm{\pi } $ , $ 2\mathrm{\pi } $ , $ 3\mathrm{\pi } $ , $ 4\mathrm{\pi } $
D. $ {\rm 0,} \dfrac{\mathrm{\pi }}{6} $ , $ \dfrac{\mathrm{\pi }}{3} $ , $ \dfrac{\mathrm{\pi }}{2} $ , $ \dfrac{2\mathrm{\pi }}{3} $
答案:A
解析: $ y=2 \sin x $ 与 $ y= \sin x $ 图象对应五点的横坐标相同,则用“五点法”作图时,对应五个点的横坐标分别为 $ {\rm 0,} \dfrac{\mathrm{\pi }}{2} $ , $ \mathrm{\pi } $ , $ \dfrac{3\mathrm{\pi }}{2} $ , $ 2\mathrm{\pi } $ .故选 $ \mathrm{A} $ .
2.已知函数 $ y=1+ \sin x $ , $ x\in [0,2\mathrm{\pi }] $ .
(1) 用五点法画函数 $ y=1+ \sin x $ , $ x\in [0,2\mathrm{\pi }] $ 的图象;
(2) 讨论函数 $ y=1+ \sin x $ , $ x\in [0,2\mathrm{\pi }] $ 图象与直线 $ y=t(t $ 为常数 $ ) $ 的交点个数.
答案:(1) 【解】由题意,列表:
$ x $ | 0 | $ \dfrac{\mathrm{\pi }}{2} $ | $ \mathrm{\pi } $ | $ \dfrac{3\mathrm{\pi }}{2} $ | $ 2\mathrm{\pi } $ |
$ \sin x $ | 0 | 1 | 0 | $ -1 $ | 0 |
$ \sin x+1 $ | 1 | 2 | 1 | 0 | 1 |
描点并将它们用光滑的曲线连接起来,如图所示.

(2) $ y=1+ \sin x $ , $ x\in [0,2\mathrm{\pi }] $ 图象如图所示:

观察图象得:当 $ t < 0 $ 或 $ t > 2 $ 时,函数 $ y=1+ \sin x $ , $ x\in [0,2\mathrm{\pi }] $ 图象与直线 $ y=t $ 有0个交点;
当 $ t=0 $ 或 $ t=2 $ 时,函数 $ y=1+ \sin x $ , $ x\in [0,2\mathrm{\pi }] $ 图象与直线 $ y=t $ 有1个交点;
当 $ 0 < t < 1 $ 或 $ 1 < t < 2 $ 时,函数 $ y=1+ \sin x $ , $ x\in [0,2\mathrm{\pi }] $ 图象与直线 $ y=t $ 有2个交点;
当 $ t=1 $ 时,函数 $ y=1+ \sin x $ , $ x\in [0,2\mathrm{\pi }] $ 图象与直线 $ y=t $ 有3个交点.
解析:
3.函数 $ f(x)= \cos x-{ \cos }^{3}x $ 的图象大致为( )
A.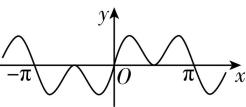
B.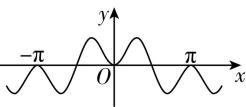
C.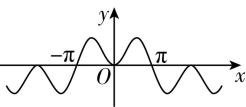
D.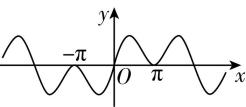
答案:B
解析: $ f(x) $ 的定义域为 $ \boldsymbol{R} $ ,且 $ f(-x)= \cos (-x)-{ \cos }^{3}(-x)= \cos x-{ \cos }^{3}x=f(x) $ ,所以 $ f(x) $ 是偶函数,故排除 $ \mathrm{A} $ , $ \mathrm{D} $ ;
当 $ x=\dfrac{5\mathrm{\pi }}{6} $ 时, $ f(\dfrac{5\mathrm{\pi }}{6})=-\dfrac{\sqrt{3}}{2}-{\left(-\dfrac{\sqrt{3}}{2}\right) ^ {3}}=-\dfrac{\sqrt{3}}{8} < 0 $ ,故排除 $ \mathrm{C} $ .故选 $ \mathrm{B} $ .
4.函数 $ f(x)=\dfrac{x \sin x}{2} $ 的图象大致为( )
A.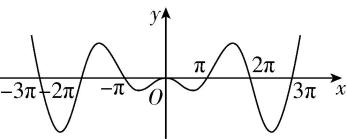
B.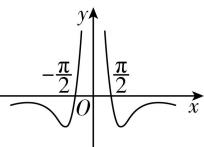
C.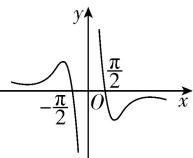
D.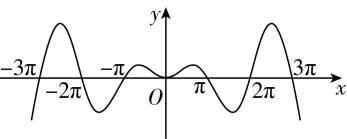
答案:D
解析:由函数 $ f(x)=\dfrac{x \sin x}{2} $ 的定义域为 $ \boldsymbol{R} $ ,关于原点对称,且满足 $ f(-x)=\dfrac{(-x) \sin (-x)}{2}=\dfrac{x \sin x}{2}=f(x) $ ,可得 $ f(x) $ 为偶函数,排除 $ \mathrm{C} $ 项;
当 $ x=\dfrac{\mathrm{\pi }}{2} $ 时,可得 $ f(\dfrac{\mathrm{\pi }}{2})=\dfrac{\mathrm{\pi }}{4} > 0 $ ,排除 $ \mathrm{A} $ , $ \mathrm{B} $ 项.故选 $ \mathrm{D} $ .
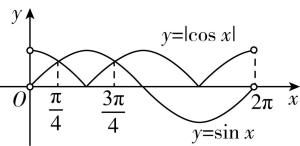
5.在 $ (0,2\mathrm{\pi }) $ 内,使 $ \sin x > | \cos x| $ 的 $ x $ 的取值范围是( )
A. $ (\dfrac{\mathrm{\pi }}{4},\dfrac{3\mathrm{\pi }}{4}) $
B. $ (\dfrac{\mathrm{\pi }}{4},\dfrac{\mathrm{\pi }}{2})\cup (\dfrac{5\mathrm{\pi }}{4},\dfrac{3\mathrm{\pi }}{2}] $
C. $ (\dfrac{\mathrm{\pi }}{4},\dfrac{\mathrm{\pi }}{2}) $
D. $ (\dfrac{5\mathrm{\pi }}{4},\dfrac{7\mathrm{\pi }}{4}) $
答案:A
解析:作出 $ y= \sin x $ 以及 $ y=| \cos x| $ 在 $ (0,2\mathrm{\pi }) $ 上的图象如图所示,由图可知,当 $ x\in (\dfrac{\mathrm{\pi }}{4},\dfrac{3\mathrm{\pi }}{4}) $ 时, $ \sin x > | \cos x| $ .故选 $ \mathrm{A} $ .
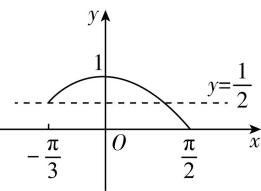
6.若函数 $ f(x)= \cos x-a $ 在 $ [-\dfrac{\mathrm{\pi }}{3} $ , $ \dfrac{\mathrm{\pi }}{2} ] $ 上有两个不同的零点,则实数 $ a $ 的取值范围是( )
A. $ [\dfrac{\sqrt{3}}{2},1) $
B. $ [\dfrac{\sqrt{3}}{2},1] $
C. $ [\dfrac{1}{2},1) $
D. $ [\dfrac{1}{2},1] $
答案:C
解析:由 $ f(x)= \cos x-a=0 $ ,得 $ a= \cos x $ ,
画出函数 $ y= \cos x $ 在区间 $ [-\dfrac{\mathrm{\pi }}{3},\dfrac{\mathrm{\pi }}{2}] $ 上的图象如图所示,
因为函数 $ f(x)= \cos x-a $ 在 $ [-\dfrac{\mathrm{\pi }}{3},\dfrac{\mathrm{\pi }}{2}] $ 上有两个不同的零点,
所以由图可知, $ a $ 的取值范围是 $ [\dfrac{1}{2},1) $ .故选 $ \mathrm{C} $ .
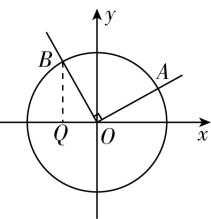
7.如图,在平面直角坐标系中,角 $ \alpha (0\leqslant \alpha \leqslant \mathrm{\pi }) $ 的始边为 $ x $ 轴的非负半轴,终边与单位圆的交点为 $ A $ ,将 $ OA $ 绕坐标原点逆时针旋转 $ \dfrac{\mathrm{\pi }}{2} $ 至 $ OB $ ,过点 $ B $ 作 $ x $ 轴的垂线,垂足为 $ \mathbf{Q} $ ,记线段 $ BQ $ 的长为 $ y $ ,则函数 $ y=f(\alpha ) $ 的图象大致是( )
A.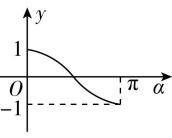
B.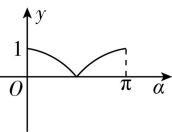
C.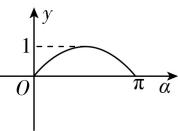
D.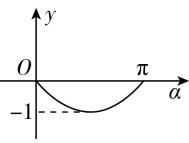
答案:B
解析:由题意,可得 $ A( \cos \alpha , \sin \alpha ) $ ,将 $ OA $ 绕坐标原点逆时针旋转 $ \dfrac{\mathrm{\pi }}{2} $ 至 $ OB $ ,
可得 $ B( \cos (\alpha +\dfrac{\mathrm{\pi }}{2}), \sin (\alpha +\dfrac{\mathrm{\pi }}{2})) $ ,即 $ B(- \sin \alpha , \cos \alpha ) $ .
因为线段 $ BQ $ 的长为 $ y $ ,所以函数 $ y=f(\alpha )=| \cos \alpha | $ ,
由余弦函数的图象可知,满足 $ y=f(\alpha ) $ 的大致图象是 $ \mathrm{B} $ 选项.故选 $ \mathrm{B} $ .
二、刷提升
1.函数 $ f(x)=\dfrac{x}{2 \cos x-1} $ , $ x\in (-\dfrac{\mathrm{\pi }}{3},\dfrac{\mathrm{\pi }}{3}) $ 的图象大致是( )
A.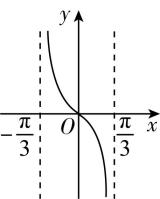
B.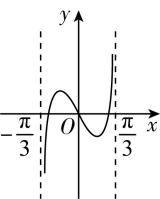
C.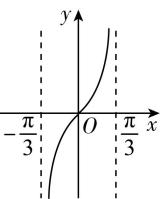
D.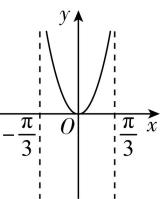
答案:C
解析: $ \because f(x)=\dfrac{x}{2 \cos x-1} $ , $ x\in (-\dfrac{\mathrm{\pi }}{3} $ , $ \dfrac{\mathrm{\pi }}{3}) $ ,
$ \therefore \forall x\in (-\dfrac{\mathrm{\pi }}{3},\dfrac{\mathrm{\pi }}{3}) $ , $ -x\in (-\dfrac{\mathrm{\pi }}{3},\dfrac{\mathrm{\pi }}{3}) $ , $ f(-x)=\dfrac{-x}{2 \cos (-x)-1}=-f(x) $ ,
$ \therefore $ 函数 $ f(x) $ 是奇函数,排除 $ \mathrm{D} $ ,
当 $ 0 < x < \dfrac{\mathrm{\pi }}{3} $ 时, $ 2 \cos x-1 > 0 $ ,则 $ f(x) > 0 $ ,排除 $ \mathrm{A} $ , $ \mathrm{B} $ .故选 $ \mathrm{C} $ .
2.记 $ [x] $ 为不超过 $ x $ 的最大整数,则方程 $ 2x-[x]= \sin x $ 的实数解的个数为( )
A.2
B.3
C.4
D.5
答案:B
解析:令 $ f(x)=2x-[x] $ , $ g(x)= \sin x $ ,则 $ 2x-[x]= \sin x $ 实数解的个数等价于 $ y=f(x) $ 与 $ y=g(x) $ 图象交点的个数.
$ f(x)=\begin{cases}\cdots ,\\ 2x+2,-2\leqslant x < -1,\\ 2x+1,-1\leqslant x < 0,\\ 2x,0\leqslant x < 1,\\ 2x-1,1\leqslant x < 2,\\ 2x-2,2\leqslant x < 3,\\ \cdots ,\end{cases} $
作出函数 $ y=f(x) $ , $ y=g(x) $ 的图象如图所示,易得两个函数的图象有3个交点,所以方程 $ 2x-[x]= \sin x $ 有3个实数解.故选 $ \mathrm{B} $ .
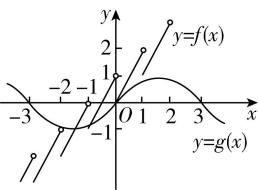
3.对于函数 $ f(x)=\begin{cases} \sin x, \sin x\geqslant \cos x,\\ \cos x, \sin x < \cos x,\end{cases} $ 下列说法中不正确的是( )(多选)
A.该函数的值域是 $ [-1,1] $
B.当且仅当 $ x=2k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2}(k\in \boldsymbol{Z}) $ 时,函数 $ f(x) $ 取得最大值1
C.当且仅当 $ x=2k\mathrm{\pi }-\dfrac{\mathrm{\pi }}{2}(k\in \boldsymbol{Z}) $ 时,函数 $ f(x) $ 取得最小值 $ -1 $
D.当且仅当 $ 2k\mathrm{\pi }+\mathrm{\pi } < x < 2k\mathrm{\pi }+\dfrac{3\mathrm{\pi }}{2}(k\in \boldsymbol{Z}) $ 时, $ f(x) < 0 $
答案:ABC
解析:画出函数 $ f(x) $ 的部分图象如图中实线所示,由图象可看出,该函数的值域是 $ [-\dfrac{\sqrt{2}}{2},1] $ ;当且仅当 $ x=2k\mathrm{\pi }+\dfrac{\mathrm{\pi }}{2} $ 或 $ x=2k\mathrm{\pi } $ , $ k\in \boldsymbol{Z} $ 时,函数 $ f(x) $ 取得最大值1;当且仅当 $ x=2k\mathrm{\pi }+\dfrac{5\mathrm{\pi }}{4} $ , $ k\in \boldsymbol{Z} $ 时,函数 $ f(x) $ 取得最小值 $ -\dfrac{\sqrt{2}}{2} $ ;当且仅当 $ 2k\mathrm{\pi }+\mathrm{\pi } < x < 2k\mathrm{\pi }+\dfrac{3\mathrm{\pi }}{2} $ , $ k\in \boldsymbol{Z} $ 时, $ f(x) < 0 $ .故 $ \mathrm{A} $ , $ \mathrm{B} $ , $ \mathrm{C} $ 不正确, $ \mathrm{D} $ 正确.
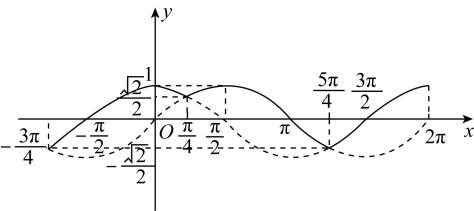
4.函数 $ f(x)= \sin x $ 在区间 $ (0,22\mathrm{\pi }) $ 上可找到 $ n $ 个不同的数 $ {x}_{1} $ , $ {x}_{2} $ , $ \cdots $ , $ {x}_{n} $ ,使得 $ \dfrac{f({x}_{1})}{{x}_{1}}=\dfrac{f({x}_{2})}{{x}_{2}}=\cdots =\dfrac{f({x}_{n})}{{x}_{n}} $ ,则 $ n $ 的最大值为( )
A.20
B.21
C.22
D.23
答案:C
解析:设 $ \dfrac{f({x}_{1})}{{x}_{1}}=\dfrac{f({x}_{2})}{{x}_{2}}=\cdots =\dfrac{f({x}_{n})}{{x}_{n}}=k $ ,则条件等价为 $ f(x)=kx $ 的根的个数,作出函数 $ f(x) $ 和 $ y=kx $ 的图象,如图所示,由图可知当 $ k < 0 $ 时,直线 $ y=kx $ 与函数 $ y=f(x) $ 的图象在 $ (0,22\mathrm{\pi }) $ 上最多有22个交点, $ k=0 $ 时,有21个交点, $ k > 0 $ 时,最多有21个交点,即 $ n $ 的最大值为22.故选 $ \mathrm{C} $ .
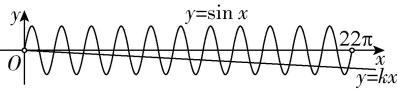
5.函数 $ y=2 \cos x $ , $ x\in [0,2\mathrm{\pi }] $ 的图象和直线 $ y=2 $ 围成的一个封闭的平面图形的面积是 .
解析:根据题意作图,如图所示.
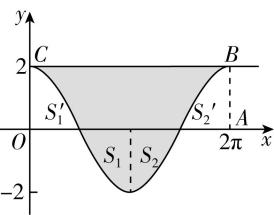
由余弦函数的性质可知,图形 $ S{\prime }_{1} $ 与 $ {S}_{1} $ , $ S{\prime }_{2} $ 与 $ {S}_{2} $ 分别是两组对称图形,
则有 $ S{\prime }_{1}={S}_{1} $ , $ S{\prime }_{2}={S}_{2} $ ,阴影部分面积等于矩形 $ OCBA $ 的面积,
根据图形可知 $ OA=2\mathrm{\pi } $ , $ OC=2 $ ,矩形 $ OCBA $ 的面积为 $ 2×2\mathrm{\pi }=4\mathrm{\pi } $ ,即封闭图形的面积为 $ 4\mathrm{\pi } $ .
6.用“五点法”作出函数 $ y=1-2 \sin x $ , $ x\in [-\mathrm{\pi } $ , $ \mathrm{\pi } ] $ 的简图,并回答下列问题:
(1) 观察函数图象,写出满足下列条件的 $ x $ 的区间 $ .\mathrm{①}y > 1 $ ; $ \mathrm{②}y < 1 $ .
(2) 若直线 $ y=a $ 与 $ y=1-2 \sin x $ , $ x\in [-\mathrm{\pi } $ , $ \mathrm{\pi } ] $ 的图象有两个交点,求实数 $ a $ 的取值范围.
答案:【解】列表如下:
$ x $ | $ -\mathrm{\pi } $ | $ {\rm -} \dfrac{\mathrm{\pi }}{2} $ | 0 | $ \dfrac{\mathrm{\pi }}{2} $ | $ \mathrm{\pi } $ |
$ \sin x $ | 0 | $ -1 $ | 0 | 1 | 0 |
$ 1-2 \sin x $ | 1 | 3 | 1 | $ -1 $ | 1 |
描点并将它们用光滑的曲线连接起来,如图所示.

(1) 【解】由图象可知,图象在直线 $ y=1 $ 上方时 $ y > 1 $ ,在直线 $ y=1 $ 下方时 $ y < 1 $ ,
所以①当 $ x\in (-\mathrm{\pi },0) $ 时, $ y > 1 $ ;②当 $ x\in (0,\mathrm{\pi }) $ 时, $ y < 1 $ .
(2) 【解】如图所示,当直线 $ y=a $ 与 $ y=1-2 \sin x $ , $ x\in [-\mathrm{\pi },\mathrm{\pi }] $ 的图象有两个交点时, $ 1 < a < 3 $ 或 $ -1 < a < 1 $ ,所以实数 $ a $ 的取值范围是 $ (-1,1)\cup (1,3) $ .
解析:
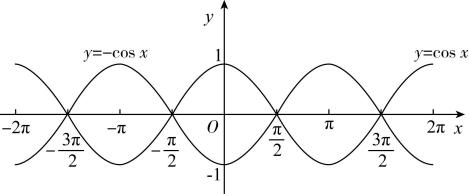
7.在同一平面直角坐标系中,函数 $ y=- \cos x $ 的图象与余弦函数 $ y= \cos x $ 的图象( )
A.只关于 $ x $ 轴对称
B.只关于原点对称
C.关于原点、 $ x $ 轴对称
D.关于原点、坐标轴对称
答案:C
解析:在同一平面直角坐标系中作出函数 $ y= \cos x $ 与函数 $ y=- \cos x $ 的简图,易知选 $ \mathrm{C} $ .
8.函数 $ f(x)= \lg x- \sin x $ 的零点个数是( )
A.1
B.2
C.3
D.4
答案:C
解析:函数 $ f(x)= \lg x- \sin x $ 的零点个数,即函数 $ y= \lg x $ 的图象与函数 $ y= \sin x $ 的图象的交点个数,由于 $ \lg 10=1 $ , $ \sin \dfrac{\mathrm{\pi }}{2}=1 $ , $ \sin \dfrac{5\mathrm{\pi }}{2}=1 $ , $ \sin \dfrac{9\mathrm{\pi }}{2}=1 $ ,
在同一坐标系中作出函数图象如图所示.
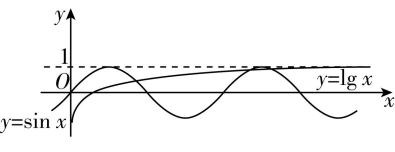
由图象可知,交点有3个.故选 $ \mathrm{C} $ .
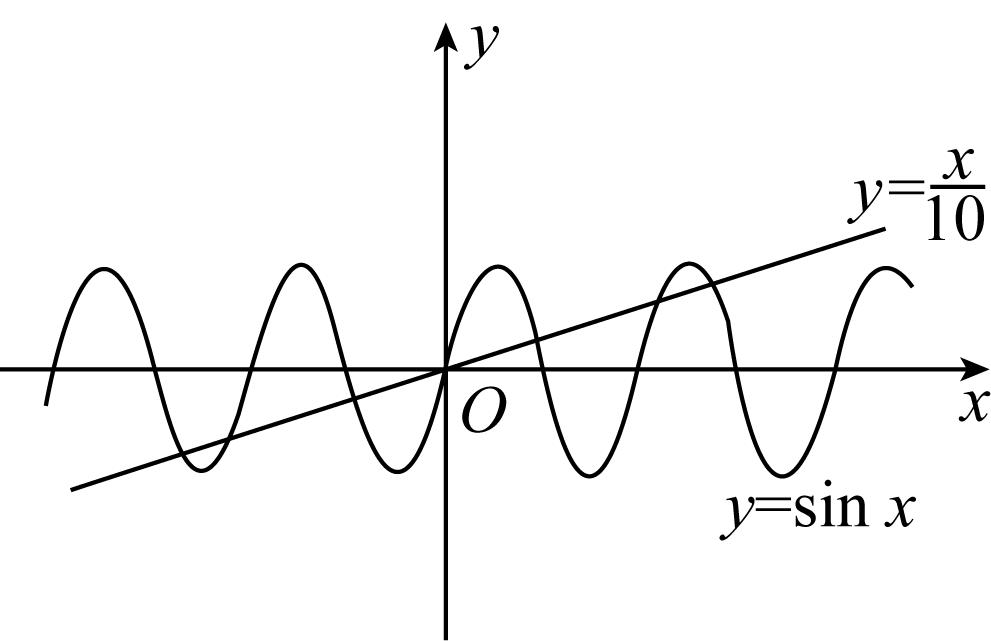
9.方程 $ 10 \sin \text{ }x=x(x\in \boldsymbol{R}) $ 根的个数是 .
解析:函数 $ y= \sin \text{ }x $ 与 $ y=\dfrac{x}{10} $ 的图象如图所示.当 $ x\geqslant 4\mathrm{\pi } $ 时, $ \dfrac{x}{10}\geqslant \dfrac{4\mathrm{\pi }}{10} > 1\geqslant \sin \text{ }x $ ;当 $ x=\dfrac{5\mathrm{\pi }}{2} $ 时, $ \sin \text{ }x= \sin \text{ }\dfrac{5\mathrm{\pi }}{2}=1 $ , $ \dfrac{x}{10}=\dfrac{\mathrm{\pi }}{4} < 1 $ ;当 $ x=\dfrac{9\mathrm{\pi }}{2} $ 时, $ \sin \text{ }x= \sin \dfrac{9\mathrm{\pi }}{2}=1 $ , $ \dfrac{x}{10}=\dfrac{9\mathrm{\pi }}{20} > 1 $ .从而当 $ x > 0 $ 时,两函数图象有3个交点.由对称性知,当 $ x < 0 $ 时,两函数图象有3个交点.当 $ x=0 $ 时的交点为原点.所以函数 $ y= \sin \text{ }x $ 与 $ y=\dfrac{x}{10} $ 的图象共有7个交点,即方程 $ 10 \sin \text{ }x=x $ 有7个根.