4.5.3 函数模型的应用
一、刷基础
1.某工厂产生的废气经过滤后排放,过滤过程中废气的污染物含量 $ P $ (单位: $ \mathrm{m}\mathrm{g}/\mathrm{L} $ )与时间 $ t $ (单位: $ \mathrm{h} $ )间的关系为 $ P={P}_{0}\cdot {\mathrm{e}}^{-kt} $ (其中 $ {P}_{0} $ , $ k $ 是正常数),如果在前 $ 5\mathrm{h} $ 消除了 $ 10\mathrm{\%} $ 的污染物,那么污染物减少 $ 50\mathrm{\%} $ 需要花费的时间约为( )
(参考数据: $ \ln 0.5\approx -0.693 $ , $ \ln 0.9\approx -0.105 $ )
A. $ 6\mathrm{h} $
B. $ 10\mathrm{h} $
C. $ 11\mathrm{h} $
D. $ 33\mathrm{h} $
答案:D
解析:根据题意可知,当 $ t=0 $ 时, $ P={P}_{0} $ 为最开始的污染物含量.当 $ t=5 $ 时,废气的污染物含量为 $ {P}_{0}\cdot {\mathrm{e}}^{-5k}=0.9{P}_{0} $ ,所以 $ {\mathrm{e}}^{-5k}=0.9 $ .所以当污染物减少 $ 50\mathrm{\%} $ 时,可设 $ {P}_{0}\cdot {\mathrm{e}}^{-kt}=0.5{P}_{0} $ .所以 $ {\mathrm{e}}^{-kt}=0.5 $ ,所以 $ {({\mathrm{e}}^{-5k})}^{\frac{t}{5}}=0.5 $ ,则 $ {0.9}^{\frac{t}{5}}=0.5 $ .所以 $ \dfrac{t}{5} \ln 0.9= \ln 0.5 $ ,所以 $ t=5×\dfrac{ \ln 0.5}{ \ln 0.9}\approx 5×\dfrac{-0.693}{-0.105}=33 $ .故选 $ \mathrm{D} $ .
2.宇宙之大,粒子之微,无处不用到数学.2023年诺贝尔物理学奖颁给了“阿秒光脉冲”,光速约为 $ 3×{10}^{8}\mathrm{m}/\mathrm{s} {\rm ,1} $ 阿秒等于 $ {10}^{-18}\mathrm{s} $ .现有一条 $ 50\mathrm{c}\mathrm{m} $ 的线段,第一次截去总长的一半,以后每次截去剩余长度的一半,若要使其长度小于光在1阿秒内走的距离,则需要截(参考数据: $ \lg 5\approx 0.70 $ , $ \lg 3\approx 0.48 $ )( )
A.30次
B.31次
C.32次
D.33次
答案:B
解析:根据已知可得,光在1阿秒内走的距离为 $ {10}^{-18}×3×{10}^{8}=3×{10}^{-10}\mathrm{m} $ .
设截 $ x $ 次后,剩余的长度为 $ f(x) $ (单位: $ \mathrm{m} $ ),则 $ f(x)=0.5×{\left(\dfrac{1}{2}\right) ^ {x}}={\left(\dfrac{1}{2}\right) ^ {x+1}} $ .
令 $ f(x) < 3×{10}^{-10} $ ,可得 $ {\left(\dfrac{1}{2}\right) ^ {x+1}} < 3×{10}^{-10} $ ,
结合函数 $ y={\left(\dfrac{1}{2}\right) ^ {x}} $ 的单调性,两边同时取对数可得
$ x+1 > { \log }_{\frac{1}{2}}(3×{10}^{-10})=\dfrac{ \lg (3×{10}^{-10})}{ \lg \dfrac{1}{2}}=\dfrac{-10+ \lg 3}{- \lg 2}=\dfrac{-10+ \lg 3}{ \lg 5-1}\approx \dfrac{-10+0.48}{0.70-1}\approx 31.73 $ ,
所以 $ x > 30.73 > 30 $ .所以应当截31次.故选 $ \mathrm{B} $ .
3.生物体死亡后,它的机体内原有的碳14含量 $ C $ 会按确定的比率衰减(称为衰减率), $ C $ 与死亡年数 $ t $ 之间的函数关系式为 $ C={0.5}^{\frac{t}{k}} $ ( $ k $ 为常数),大约每经过5 730年衰减为原来的一半,这个时间称为“半衰期”.若2022年某遗址文物出土时碳14的残余量约为原始量的 $ 85\mathrm{\%} $ ,则可推断该文物属于参考数据: $ { \log }_{20.85}\approx -0.23 $ ;
参考时间轴:

( )
A.战国
B.汉
C.唐
D.宋
答案:C
解析:当 $ t=5\text{ }730 $ 时, $ C=\dfrac{1}{2} $ ,故 $ 0.5={0.5}^{\frac{5\text{ }730}{k}} $ ,解得 $ k=5\text{ }730 $ ,所以 $ C={0.5}^{\frac{t}{5\text{ }730}} $ .
由题意得 $ {0.5}^{\frac{t}{5\text{ }730}}=0.85 $ , $ \dfrac{t}{5\text{ }730}=-{ \log }_{20.85}\approx 0.23 $ ,解得 $ t\approx 1\text{ }318 $ ,
而 $ 2\text{ }022-1\text{ }318=704 $ ,则可推断该文物属于唐.故选 $ \mathrm{C} $ .
4.物体在常温下的温度变化可以用牛顿冷却规律来描述:设物体的初始温度是T0,经过一定时间t(单位:min)后的温度是T,则 $ {\rm \mathit{T}-\mathit{T}\mathit{_{a}}=(\mathit{T}_{0}-\mathit{T}\mathit{_{a}})} {(\dfrac{1}{2})}^{\frac{t}{ℎ}} $ ,其中Ta称为环境温度,h为常数.现有一杯用85 ℃的热水冲的速溶咖啡,放在21 ℃的房间中,如果咖啡降到37 ℃需要16 min,那么这杯咖啡要从37 ℃降到25 ℃,还需要 min.
解析:由题意知Ta=21 ℃.令T0=85 ℃,T=37 ℃,得 $ {\rm 37-21=(85-21)·} {(\dfrac{1}{2})}^{\frac{16}{ℎ}} $ ,解得h=8.令T0=37 ℃,T=25 ℃,则 $ {\rm 25-21=(37-21)·} {(\dfrac{1}{2})}^{\frac{t}{8}} $ ,解得t=16.
5.某公司制定了一个激励销售人员的奖励方案:当销售利润不超过8万元时,按销售利润的 $ 15\mathrm{\%} $ 进行奖励;当销售利润超过8万元时,若超过多出的部分为 $ A $ 万元,则多出的部分按 $ { \log }_{5}(2A+1) $ 进行奖励.记奖金为 $ y $ (单位:万元),销售利润为 $ x $ (单位:万元).如果业务员小江获得3.2万元的奖金,那么他的销售利润是( )
A.15万元
B.25万元
C.30万元
D.20万元
答案:D
解析:由题意知,当 $ 0\leqslant x\leqslant 8 $ 时, $ y=0.15x $ ;
当 $ x > 8 $ 时, $ y=8×0.15+{ \log }_{5}[2(x-8)+1]=1.2+{ \log }_{5}(2x-15) $ ,
所以 $ y=\begin{cases}0.15x,0\leqslant x\leqslant 8,\\ 1.2+{ \log }_{5}(2x-15),x > 8,\end{cases} $
当 $ 0\leqslant x\leqslant 8 $ 时, $ {y}_{ \max }=0.15×8=1.2 < 3.2 $ ,故小江的销售利润 $ x > 8 $ ,
所以 $ 1.2+{ \log }_{5}(2x-15)=3.2 $ ,解得 $ x=20 $ ,
所以小江的销售利润是20万元.故选 $ \mathrm{D} $ .
6.中国的 $ 5\mathrm{G} $ 技术领先世界, $ 5\mathrm{G} $ 技术的数学原理之一便是著名的香农公式 $ C=W{ \log }_{2}(1+\dfrac{S}{N}) $ ,它表示在受噪声干扰的信道中,最大信息传递速率 $ C $ 取决于信道带宽 $ W $ 、信道内信号的平均功率 $ S $ 、信道内部的高斯噪声功率 $ N $ 的大小,其中 $ \dfrac{S}{N} $ 叫做信噪比.当信噪比比较大时,公式的真数中的1可以忽略不计.按照香农公式,由于技术提升,信道带宽 $ W $ 在原来的基础上增加 $ 20\mathrm{\%} $ ,信噪比 $ \dfrac{S}{N} $ 从1 000提升至 $ 4\text{ }000 $ ,则 $ C $ 大约增加了( )
(参考数据: $ \lg \text{ }5\approx 0.699\text{ }0 $ )
A. $ 22\mathrm{\%} $
B. $ 33\mathrm{\%} $
C. $ 44\mathrm{\%} $
D. $ 55\mathrm{\%} $
答案:C
解析:由题意可知, $ C $ 大约增加了
$ \dfrac{120\mathrm{\%}W{ \log }_{24}\text{ }000-W{ \log }_{21}\text{ }000}{W{ \log }_{21}\text{ }000} $
$ =\dfrac{1.2{ \log }_{24}\text{ }000}{{ \log }_{21}\text{ }000}-1\text{ }=1.2{ \log }_{1\text{ }000}4\text{ }000-1=0.4 \lg \text{ }4\text{ }000-1\text{ }=0.4(3+2 \lg \text{ }2)-1\text{ }=0.2+0.8(1- \lg \text{ }5)\approx 0.440\text{ }8 $ .
故选 $ \mathrm{C} $ .
7.(多选)研究表明,地震时释放的能量 $ E $ (单位: $ \mathrm{J} $ )与地震里氏震级 $ M $ 之间的关系为 $ \lg E=4.8+1.5M $ ,则( )(多选)
A.震级为2级的地震释放的能量为 $ {10}^{6.8}\mathrm{J} $
B.释放能量为 $ {10}^{9.3}\mathrm{J} $ 的地震震级为3级
C.9级地震释放的能量是8级地震释放的能量的10倍
D.释放能量之比为 $ 1000:1 $ 的两场地震的震级相差2级
答案:BD
解析:对于 $ \mathrm{A} $ ,当 $ M=2 $ 时, $ \lg E=4.8+1.5×2=7.8 $ ,解得 $ E={10}^{7.8} $ , $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,当 $ E={10}^{9.3} $ 时, $ 9.3=4.8+1.5M $ ,解得 $ M=3 $ , $ \mathrm{B} $ 正确;
对于 $ \mathrm{C} $ ,令9级地震释放的能量为 $ {E}_{1} {\rm ,8} $ 级地震释放的能量为 $ {E}_{2} $ ,
则 $ \lg \dfrac{{E}_{1}}{{E}_{2}}= \lg {E}_{1}- \lg {E}_{2}=(4.8+1.5×9)-(4.8+1.5×8)=1.5 $ ,于是 $ \dfrac{{E}_{1}}{{E}_{2}}{=10}^{1.5} > 10 $ , $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,设释放的能量为 $ {E}_{0} $ ,对应的震级为 $ {M}_{0} $ ,释放的能量为 $ 1000{E}_{0} $ ,对应的震级为 $ M\prime $ ,
则 $ \lg {E}_{0}=4.8+1.5{M}_{0} $ ,且 $ \lg (1000{E}_{0})=4.8+1.5M\prime $ ,两式相减得 $ 1.5(M\prime -{M}_{0})=3 $ ,解得 $ M\prime -{M}_{0}=2 $ , $ \mathrm{D} $ 正确.故选 $ \mathrm{B}\mathrm{D} $ .
8.某地西红柿从2月1日起开始上市.通过市场调查,得到西红柿种植成本 $ Q $ (单位:元/ $ {10}^{2}\mathrm{k}\mathrm{g} $ )与上市时间 $ t $ (单位:天)的数据如下表:
时间 $ t $ | 50 | 110 | 250 |
种植成本 $ Q $ | 150 | 108 | 150 |
根据上表数据,函数 $ \mathrm{①}Q=at+b $ , $ \mathrm{②}Q=a{t}^{2}+bt+c $ , $ \mathrm{③}Q=a\cdot {b}^{t} $ , $ \mathrm{④}Q=a{ \log }_{b}t $ .能够描述西红柿种植成本 $ \mathbf{Q} $ 与上市时间 $ t $ 的变化关系的是( )
A.①
B.②
C.③
D.④
答案:B
解析:根据题中表格数据,西红柿种植成本 $ \mathbf{Q} $ 与上市时间 $ t $ 的变化关系不是常函数,也不是单调函数,
而 $ \mathbf{Q}=at+b $ , $ \mathbf{Q}=a\cdot {b}^{t} $ , $ \mathbf{Q}=a{ \log }_{b}t $ ,在 $ a\ne 0 $ 时,均为单调函数,这与所提供的数据不符,
故能够描述西红柿种植成本 $ Q $ 与上市时间 $ t $ 的变化关系的是 $ Q=a{t}^{2}+bt+c $ ,
故选 $ \mathrm{B} $ .
9.为践行“绿水青山,就是金山银山”的理念,某省决定净化闽江上游水域的水质.省环保局于2023年年底在闽江上游水域投入一些蒲草,这些蒲草在水中的蔓延速度越来越快,2024年2月底测得蒲草覆盖面积为 $ 36{\mathrm{m}}^{2} {\rm ,2024} $ 年3月底测得蒲草覆盖面积为 $ 48{\mathrm{m}}^{2} $ ,蒲草覆盖面积 $ y $ (单位: $ {\mathrm{m}}^{2} $ )与月份 $ x $ (单位:月)的关系有两个函数模型 $ y=k{a}^{x}(k > 0,a > 1) $ 与 $ y=m{x}^{2}+n(m > 0) $ 可供选择.
(1) 分别求出两个函数模型的解析式;
(2) 若2023年年底测得蒲草覆盖面积为 $ 20{\mathrm{m}}^{2} $ ,从上述两个函数模型中选择更合适的一个模型,说明理由,并估算至少到哪一年的几月底蒲草覆盖面积能达到 $ 810{\mathrm{m}}^{2} $ .(参考数据: $ \lg 2\approx 0.30 $ , $ \lg 3\approx 0.48 $ )
答案:(1) 【解】若选择模型 $ y=k{a}^{x}(k > 0,a > 1) $ ,则 $ \begin{cases}k{a}^{2}=36,\\ k{a}^{3}=48,\end{cases} $ 解得 $ a=\dfrac{4}{3} $ , $ k=\dfrac{81}{4} $ ,
故函数模型为 $ y=\dfrac{81}{4}\cdot {\left(\dfrac{4}{3}\right) ^ {x}} $ .
若选择模型 $ y=m{x}^{2}+n(m > 0) $ ,则 $ \begin{cases}4m+n=36,\\ 9m+n=48,\end{cases} $ 解得 $ m=\dfrac{12}{5} $ , $ n=\dfrac{132}{5} $ ,
故函数模型为 $ y=\dfrac{12}{5}{x}^{2}+\dfrac{132}{5} $ .
(2) 【解】把 $ x=0 $ 代入 $ y=\dfrac{81}{4}\cdot {\left(\dfrac{4}{3}\right) ^ {x}} $ ,可得 $ y=\dfrac{81}{4}=20.25 $ ,
把 $ x=0 $ 代入 $ y=\dfrac{12}{5}{x}^{2}+\dfrac{132}{5} $ ,可得 $ y=\dfrac{132}{5} $ ,可知 $ \dfrac{132}{5} $ 与20相差比较大,
故选择函数模型 $ y=\dfrac{81}{4}\cdot {\left(\dfrac{4}{3}\right) ^ {x}} $ 更合适.
令 $ \dfrac{81}{4}\cdot {\left(\dfrac{4}{3}\right) ^ {x}}\geqslant 810 $ ,可得 $ {\left(\dfrac{4}{3}\right) ^ {x}}\geqslant 40 $ ,两边取常用对数可得 $ x \lg \dfrac{4}{3}\geqslant \lg 40 $ ,
即 $ x\geqslant \dfrac{ \lg 40}{ \lg \dfrac{4}{3}}=\dfrac{2 \lg 2+1}{2 \lg 2- \lg 3}\approx \dfrac{2×0.3+1}{2×0.3-0.48}\approx 13.33 $ ,
故至少到2025年2月底蒲草覆盖面积能达到 $ 810{\mathrm{m}}^{2} $ .
解析:
10.某城市现有人口总数为100万,如果年自然增长率为 $ 1.2\mathrm{\%} $ ,试解答下面的问题:
(1) 写出 $ x $ 年后该城市的人口总数 $ y $ (万)与年数 $ x $ (年)的函数关系式;
(2) 计算10年后该城市人口总数(精确到0.1万);
(3) 计算大约多少年以后该城市人口总数将达到120万(精确到1年).
$ ( $ 本题参考数据: $ (1+1.2\mathrm{\%})^{10}\approx 1.127 $ , $ (1+1.2\mathrm{\%})^{15}\approx 1.196 $ , $ (1+1.2\mathrm{\%})^{16}\approx 1.21) $
答案:(1) 【解】1年后该城市人口总数为 $ y=100+100×1.2\mathrm{\%}=100×(1+1.2\mathrm{\%}) $ ;
2年后该城市人口总数为 $ y=100× (1+1.2\mathrm{\%} )+100× (1+1.2\mathrm{\%} )×1.2\mathrm{\%}=100× (1+1.2\mathrm{\%})^{2} $ ;
3年后该城市人口总数为 $ y=100×(1+1.2\mathrm{\%})^{3} $ ;……;
$ x $ 年后该城市人口总数为 $ y=100×(1+1.2\mathrm{\%})^{x} $ , $ x\in {\boldsymbol{N}}^{\ast } $ .
(2) 【解】10年后该城市人口总数为 $ y=100×(1+1.2\mathrm{\%})^{10}\approx 112.7 $ (万).
(3) 【解】令 $ y=120 $ ,则有 $ 100×(1+1.2\mathrm{\%})^{x}=120 $ ,解方程可得 $ 15 < x < 16 $ .
故大约16年后该城市人口总数将达到120万.
解析:
二、刷提升
1.据你估计,一种商品在销售收入不变的条件下,其销量 $ y $ 与价格 $ x $ 之间的关系最可能是下图中的( )
A.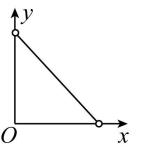
B.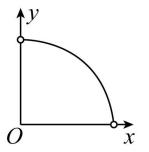
C.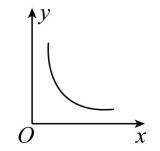
D.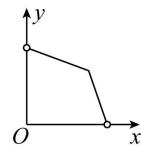
答案:C
解析:设销售收入为 $ c $ , $ \because $ 销售收入不变, $ \therefore xy=c $ (定值), $ \therefore y=\dfrac{c}{x} $ .故选 $ \mathrm{C} $ .
2.“红豆生南国,春来发几枝”,如图给出了红豆生长时间 $ x $ (月)与枝数 $ y $ (枝)的散点图 $ ( $ 直角坐标系中作出 $ (x,y) $ 对应的点 $ ) $ ,那么最符合红豆的枝数与生长时间的关系的函数是( )

A.指数函数 $ y={2}^{x} $
B.对数函数 $ y={ \log }_{2}x $
C.幂函数 $ y={x}^{3} $
D.二次函数 $ y=2{x}^{2} $
答案:A
解析:通过图象上的点可以发现,在第一象限从左到右图象是上升的,并且增长速度越来越快,图象上的点大致都在函数 $ y={2}^{x} $ 的图象上,所以指数函数最符合.
3.据统计,第 $ x $ 年某湿地公园越冬的白鹭数量 $ y $ (只)近似满足 $ y=k{ \log }_{3}(x+1) $ ,观测发现第2年有越冬白鹭1 000只,估计第5年有越冬白鹭 $ ( \ln \text{ }2\approx 0.7, \ln \text{ }3\approx 1.1) $ ( )
A.1 530只
B.1 630只
C.1 830只
D.1 930只
答案:B
解析: $ \because $ 第 $ x $ 年某湿地公园越冬的白鹭数量 $ y $ (只)近似满足 $ y=k{ \log }_{3}(x+1) $ , $ x=2 $ 时, $ y=1\text{ }000 $ , $ \text{ }\therefore 1\text{ }000=k{ \log }_{3}3 $ ,解得 $ k=1\text{ }000 $ .
$ \therefore $ 当 $ x=5 $ 时, $ y=1\text{ }000{ \log }_{3}6=1\text{ }000×({ \log }_{3}3+{ \log }_{3}2)=1\text{ }000×(1+\dfrac{ \ln \text{ }2}{ \ln \text{ }3})\approx 1\text{ }636 $ .故选 $ \mathrm{B} $ .
4.近年来纯电动汽车越来越受消费者的青睐,新型动力电池迎来了蓬勃发展的风口, $ \mathrm{P}\mathrm{e}\mathrm{u}\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{t} $ 于1898年提出蓄电池的容量 $ C $ (单位: $ \mathrm{A}\mathrm{h} $ )、放电时间 $ t $ (单位: $ \mathrm{h} $ )与放电电流 $ I $ (单位:A)之间关系的经验公式: $ C={I}^{n}\cdot t $ ,其中 $ n $ 为 $ \mathrm{P}\mathrm{e}\mathrm{u}\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{t} $ 常数.为测算某蓄电池的 $ \mathrm{P}\mathrm{e}\mathrm{u}\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{t} $ 常数 $ n $ ,在电池容量不变的条件下,当放电电流 $ I=60\mathrm{A} $ 时,放电时间 $ t=30\mathrm{h} $ ;当放电电流 $ I=80\mathrm{A} $ 时,放电时间 $ t=16\mathrm{h} $ .若计算时取 $ \lg 2\approx 0.3 $ , $ \lg 3\approx 0.477 $ ,则该蓄电池的 $ \mathrm{P}\mathrm{e}\mathrm{u}\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{t} $ 常数 $ n $ 大约为 .(精确到0.01)
解析:由题意知 $ C={60}^{n}×30={80}^{n}×16 $ ,
所以 $ {\left(\dfrac{60}{80}\right) ^ {n}}={\left(\dfrac{3}{4}\right) ^ {n}}=\dfrac{16}{30}=\dfrac{8}{15} $ ,两边取以10为底的对数,得 $ n \lg \dfrac{3}{4}= \lg \dfrac{8}{15} $ ,
所以 $ n=\dfrac{ \lg \dfrac{8}{15}}{ \lg \dfrac{3}{4}}=\dfrac{ \lg 8- \lg 15}{ \lg 3- \lg 4}=\dfrac{4 \lg 2- \lg 3-1}{ \lg 3-2 \lg 2}\approx \dfrac{4×0.3-0.477-1}{0.477-2×0.3}\approx 2.25 $ .
5.舆论场指数是一个反映特定时间内社会舆论关注热点和趋势的指标,它通常通过大数据分析技术,对来自不同媒体平台的信息进行收集、整理和分析,从而得出一个量化的指数,以揭示公众对某些事件或话题的关注程度.对于舆论事件出现的第 $ x $ 天,若某次舆情过程中至少有一天的舆论场指数大于 $ t×{9}^{x} $ ,则认为本次舆情是严重的.某购物平台利用舆论场指数就某次舆情进行分析,将舆论事件出现的第1,2,3天的舆论场指数整理成如下表格:
为研究舆论场指数的变化情况,技术人员提出了三种函数模型用以刻画数据: $ \mathrm{①}y=ax+\dfrac{b}{x}+c $ ; $ \mathrm{②}y=p{ \log }_{q}x+g $ ; $ \mathrm{③}y=m×{n}^{x}+s $ 其中含 $ x $ 的项的系数均不为0.
(1) 请从①,②,③中选择一个最合适的函数模型(直接写结果,不用证明);
(2) 运用(1)中选取的函数模型,预测第4天的舆论场指数;
(3) 若本次舆情不是严重的,求 $ t $ 的最小值.
答案:(1) 【解】选③,
根据表格中数据可以看出舆论场指数增长非常快,符合指数函数性质,故选③.
(2) 【解】将表格数据代入 $ y=m×{n}^{x}+s $ ,得 $ \begin{cases}m\cdot n+s=12,\\ m\cdot {n}^{2}+s=48,\\ m\cdot {n}^{3}+s=156,\end{cases} $ 解得 $ \begin{cases}m=6,\\ n=3,\\ s=-6,\end{cases} $
故函数模型为 $ y=6×{3}^{x}-6 $ ,
则第4天的舆论场指数为 $ 6×{3}^{4}-6=480 $ .
(3) 【解】若本次舆情不是严重的,则 $ 6×{3}^{x}-6\leqslant t×{9}^{x} $ 恒成立,
则 $ 6×{3}^{x}-6\leqslant t×{3}^{2x} $ ,故两边同时除以 $ {3}^{2x} $ ,得 $ \dfrac{6}{{3}^{x}}-\dfrac{6}{{3}^{2x}}\leqslant t $ ,
不妨设 $ k=\dfrac{1}{{3}^{x}} $ , $ k\in (0,\dfrac{1}{3}] $ ,则 $ \dfrac{6}{{3}^{x}}-\dfrac{6}{{3}^{2x}}\leqslant t $ 可化为 $ 6k-6{k}^{2}\leqslant t $ ,整理得 $ 6{k}^{2}-6k+t\geqslant 0 $ ,
由于 $ y=6{k}^{2}-6k+t $ 在 $ k\in (0,\dfrac{1}{3}] $ 上单调递减,故只需要当 $ k=\dfrac{1}{3} $ 时, $ 6{k}^{2}-6k+t\geqslant 0 $ 成立即可,
代入得 $ \dfrac{2}{3}-2+t\geqslant 0 $ ,解得 $ t\geqslant \dfrac{4}{3} $ ,
故 $ t $ 的最小值为 $ \dfrac{4}{3} $ .
解析:





