1.4.1 充分条件与必要条件+1.4.2 充要条件
一、刷基础
1.下列说法正确的是( )
A.“ $ ac=bc $ ”是“ $ a=b $ ”的充分条件
B.“ $ x\geqslant 1 $ ”是“ $ {x}^{2}\geqslant 1 $ ”的必要条件
C.“四边形对角线互相垂直”是“四边形为菱形”的充要条件
D.“ $ 1 < x < 3 $ ”是“ $ x\geqslant 0 $ ”的充分不必要条件
答案:D
解析:对于 $ \mathrm{A} $ ,当 $ c=0 $ 时,满足 $ ac=bc $ ,但此时存在 $ a\ne b $ 的情况,故 $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ , $ {x}^{2}\geqslant 1 $ 等价于 $ x\geqslant 1 $ 或 $ x\leqslant -1 $ ,故“ $ x\geqslant 1 $ ”是“ $ {x}^{2}\geqslant 1 $ ”的充分不必要条件,故 $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,“四边形对角线互相垂直”是“四边形为菱形”的必要不充分条件,故 $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,“ $ 1 < x < 3 $ ”是“ $ x\geqslant 0 $ ” 的充分不必要条件,故 $ \mathrm{D} $ 正确.
故选 $ \mathrm{D} $ .
2.子曰:“工欲善其事,必先利其器.”这句名言最早出自《论语·卫灵公》.此名言中的“利其器”是“善其事”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:B
解析:由题意“工欲善其事,必先利其器.”指工匠要想做好活儿,一定先要把工具整治得锐利精良.
从逻辑角度理解,如果工匠做好活了,说明肯定是有锐利精良的工具,即必要性成立;
反过来如果有锐利精良的工具,不能得出一定能做好活儿,即充分性不成立.
所以“利其器”是“善其事”的必要不充分条件.故选 $ \mathrm{B} $ .
3.“ $ m < \dfrac{1}{4} $ ”是“一元二次方程 $ {x}^{2}+x+m=0 $ 有实数解”的 条件.(填“充要”“充分不必要”“必要不充分”或“既不充分也不必要”)
解析:一元二次方程 $ {x}^{2}+x+m=0 $ 有实数解 $ ⇔\mathrm{\Delta }=1-4m\geqslant 0 $ ,即 $ m\leqslant \dfrac{1}{4} $ .因为 $ m < \dfrac{1}{4}⇒m\leqslant \dfrac{1}{4} $ ,反之不成立,所以“ $ m < \dfrac{1}{4} $ ”是“一元二次方程 $ {x}^{2}+x+m=0 $ 有实数解”的充分不必要条件.
4.已知 $ U $ 为全集,集合 $ A $ , $ B $ 为 $ U $ 的两个子集,则“ $ A\subseteq {\complement }_{U}B $ ”的充要条件是( )
A. $ B\subseteq {\complement }_{U}A $
B. $ A\subseteq B $
C. $ B\subseteq A $
D. $ {\complement }_{U}A\subseteq B $
答案:A
解析:因为 $ A\subseteq {\complement }_{U}B $ ,则 $ A $ , $ B $ 间的关系如图,
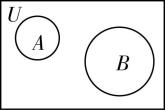 或
或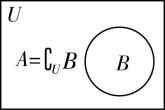
由图可知 $ \mathrm{B} $ , $ \mathrm{C} $ , $ \mathrm{D} $ 错误, $ \mathrm{A} $ 正确.故选 $ \mathrm{A} $ .
5.若 $ x $ , $ y\in \boldsymbol{R} $ ,则“ $ x > y $ ”的一个充分不必要条件可以是( )
A. $ |x| > |y| $
B. $ {x}^{2} > {y}^{2} $
C. $ \dfrac{x}{y} > 1 $
D. $ x-y > 1 $
答案:D
解析:对于 $ \mathrm{A} $ ,由 $ |x| > |y| $ ,取 $ x=-2 $ , $ y=1 $ ,则 $ x < y $ ,由 $ x > y $ ,取 $ x=1 $ , $ y=-2 $ ,则 $ |x| < |y| $ ,所以“ $ |x| > |y| $ ”是“ $ x > y $ ”的既不充分也不必要条件, $ \mathrm{A} $ 错误;
对于 $ \mathrm{B} $ ,由 $ {x}^{2} > {y}^{2} $ ,取 $ x=-2 $ , $ y=1 $ ,则 $ x < y $ ,由 $ x > y $ ,取 $ x=1 $ , $ y=-2 $ ,则 $ {x}^{2} < {y}^{2} $ ,
所以“ $ {x}^{2} > {y}^{2} $ ”是“ $ x > y $ ”的既不充分也不必要条件, $ \mathrm{B} $ 错误;
对于 $ \mathrm{C} $ ,由 $ \dfrac{x}{y} > 1 $ ,取 $ x=-2 $ , $ y=-1 $ ,则 $ x < y $ ,由 $ x > y $ ,取 $ x=1 $ , $ y=-2 $ ,则 $ \dfrac{x}{y} < 1 $ ,
所以“ $ \dfrac{x}{y} > 1 $ ”是“ $ x > y $ ”的既不充分也不必要条件, $ \mathrm{C} $ 错误;
对于 $ \mathrm{D} $ ,因为 $ x-y > 1 $ ,所以 $ x > y+1 > y $ ,即 $ x > y $ ,当 $ x > y $ 时,取 $ x=2.5 $ , $ y=2 $ ,则 $ x-y < 1 $ ,
所以“ $ x-y > 1 $ ”是“ $ x > y $ ”的一个充分不必要条件, $ \mathrm{D} $ 正确.
故选 $ \mathrm{D} $ .
6.(多选)“关于 $ x $ 的方程 $ {x}^{2}+mx+1=0 $ 至多有一个实数根”的必要条件可以是( )(多选)
A. $ -2\leqslant m\leqslant 2 $
B. $ -2\leqslant m\leqslant 4 $
C. $ m < 4 $
D. $ -1\leqslant m < 2 $
答案:ABC
解析:因为方程 $ {x}^{2}+mx+1=0 $ 至多有一个实数根,
所以方程 $ {x}^{2}+mx+1=0 $ 的判别式 $ \mathrm{\Delta }\leqslant 0 $ ,即 $ {m}^{2}-4\leqslant 0 $ ,解得 $ -2\leqslant m\leqslant 2 $ .
利用必要条件的定义,结合选项可知, $ -2\leqslant m\leqslant 2 $ 成立的必要条件可以是选项 $ \mathrm{A} $ , $ \mathrm{B} $ , $ \mathrm{C} $ ,故选 $ \mathrm{A}\mathrm{B}\mathrm{C} $ .
7.设计如图所示的四个电路图,若 $ p\text{:} $ 开关 $ \mathrm{S} $ 闭合, $ q\text{:} $ 灯泡 $ \mathrm{L} $ 亮,则满足 $ p $ 是 $ q $ 的充要条件的电路图是( )(多选)
A.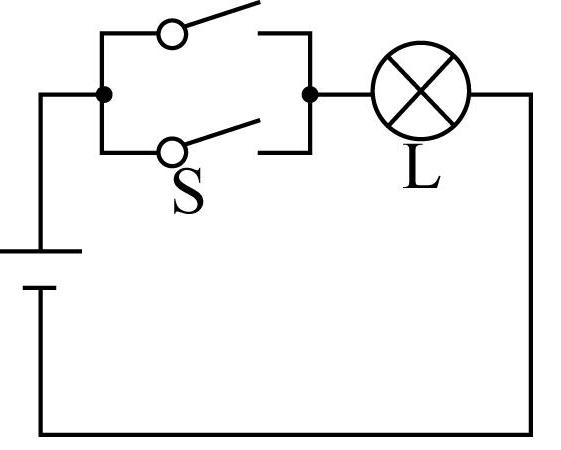
B.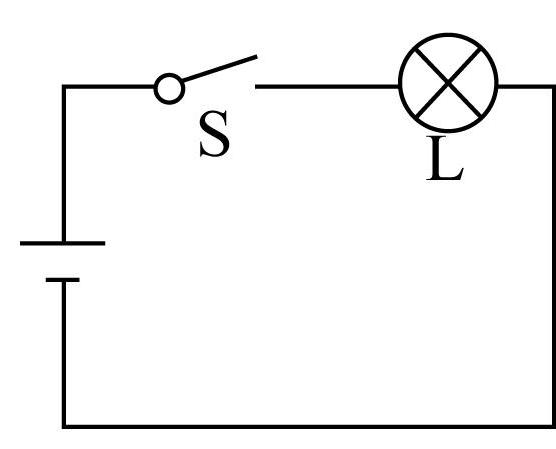
C.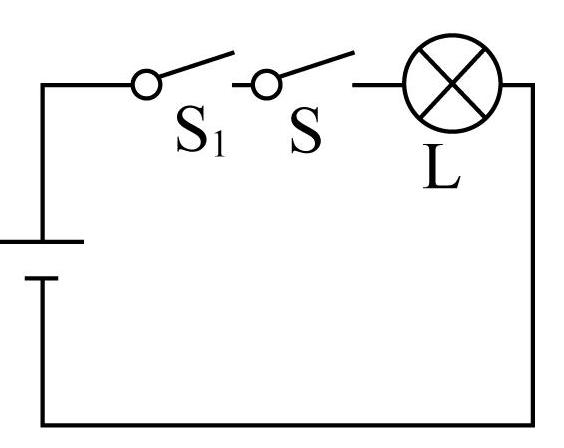
D.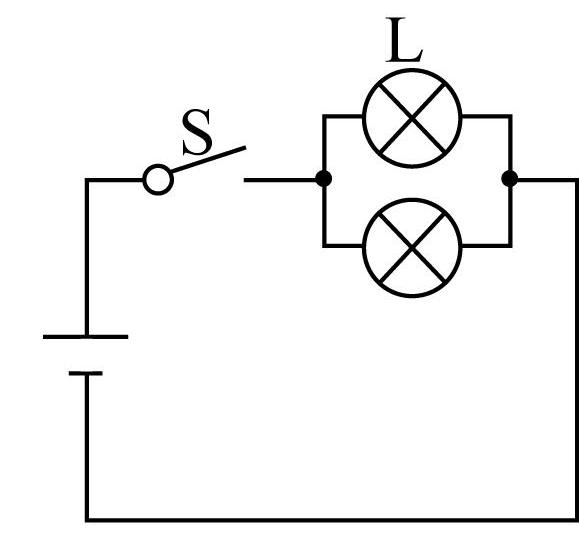
答案:BD
解析:由题知,电路图A中,开关 $ \mathrm{S} $ 闭合,灯泡 $ \mathrm{L} $ 亮,而灯泡 $ \mathrm{L} $ 亮开关 $ \mathrm{S} $ 不一定闭合,故 $ \mathrm{A} $ 中 $ p $ 是 $ q $ 的充分不必要条件;
电路图B中,开关 $ \mathrm{S} $ 闭合,灯泡 $ \mathrm{L} $ 亮,且灯泡 $ \mathrm{L} $ 亮,则开关 $ \mathrm{S} $ 一定闭合,故 $ \mathrm{B} $ 中 $ p $ 是 $ q $ 的充要条件;
电路图C中,开关 $ \mathrm{S} $ 闭合,灯泡 $ \mathrm{L} $ 不一定亮,灯泡 $ \mathrm{L} $ 亮,则开关 $ \mathrm{S} $ 一定闭合,故 $ \mathrm{C} $ 中 $ p $ 是 $ q $ 的必要不充分条件;
电路图D中,开关 $ \mathrm{S} $ 闭合,灯泡 $ \mathrm{L} $ 亮,灯泡 $ \mathrm{L} $ 亮,则一定有开关 $ \mathrm{S} $ 闭合,故 $ \mathrm{D} $ 中 $ p $ 是 $ q $ 的充要条件.故选 $ \mathrm{B}\mathrm{D} $ .
8.若集合 $ A={x|x > 2} $ , $ B={x|x < b $ , $ b\in \boldsymbol{R}} $ ,试写出 $ A\cup B=\boldsymbol{R} $ 的一个必要不充分条件.
答案:【解】由 $ A\cup B=\boldsymbol{R} $ ,得 $ b > 2 $ ,所以 $ A\cup B=\boldsymbol{R} $ 的一个必要不充分条件可以是 $ b > 1 $ (答案不唯一).
解析:
9.设 $ p:\dfrac{1}{2}\leqslant x\leqslant 1 $ ; $ q:a\leqslant x\leqslant a+1 $ ,若 $ p $ 是 $ q $ 的充分不必要条件,则实数 $ a $ 的取值范围是( )
A. $ {a|0\leqslant a\leqslant \dfrac{1}{2}} $
B. $ {a|0 < a < \dfrac{1}{2}} $
C. $ {a|a\leqslant 0或a\geqslant \dfrac{1}{2}} $
D. $ {a|a < 0或a > \dfrac{1}{2}} $
答案:A
解析:若 $ p $ 是 $ q $ 的充分不必要条件,则 $ \begin{cases}a\leqslant \dfrac{1}{2},\\ a+1\geqslant 1,\end{cases} $ 且等号不同时成立,解得 $ 0\leqslant a\leqslant \dfrac{1}{2} $ .故选 $ \mathrm{A} $ .
10.若不等式 $ |x-a| < 1 $ 成立的一个充分不必要条件是 $ \dfrac{1}{2} < x < \dfrac{3}{2} $ ,则实数 $ a $ 的取值范围是( )
A. $ {a|\dfrac{1}{2} < a < \dfrac{3}{2}} $
B. $ {a|\dfrac{1}{2}\leqslant a\leqslant \dfrac{3}{2}} $
C. $ {a|a < \dfrac{1}{2}或a > \dfrac{3}{2}} $
D. $ {a|a\leqslant \dfrac{1}{2}或a\geqslant \dfrac{3}{2}} $
答案:B
解析:由 $ |x-a| < 1 $ 解得 $ a-1 < x < 1+a $ ,所以 $ a-1 < x < 1+a $ 成立的一个充分不必要条件是 $ \dfrac{1}{2} < x < \dfrac{3}{2} $ ,故 $ {x|\dfrac{1}{2} < x < \dfrac{3}{2}} $ 是 $ {x|a-1 < x < 1+a} $ 的真子集,所以 $ \begin{cases}a-1\leqslant \dfrac{1}{2},\\ a+1 > \dfrac{3}{2}\end{cases} $ 或 $ \begin{cases}a-1 < \dfrac{1}{2},\\ a+1\geqslant \dfrac{3}{2},\end{cases} $ 解得 $ \dfrac{1}{2}\leqslant a\leqslant \dfrac{3}{2} $ ,故实数 $ a $ 的取值范围是 $ {a|\dfrac{1}{2}\leqslant a\leqslant \dfrac{3}{2}} $ .故选 $ \mathrm{B} $ .
11.已知集合 $ A={x|{x}^{2}-4=0} $ , $ B={x|ax-2=0} $ ,若 $ x\in A $ 是 $ x\in B $ 的必要不充分条件,则实数 $ a $ 的所有可能取值构成的集合为 .
答案: $ {-1 {\rm ,0} $ , $ 1} $
解析:依题意, $ A={x|{x}^{2}-4=0}={2 $ , $ -2} $ .
由 $ x\in A $ 是 $ x\in B $ 的必要不充分条件,得 $ B⫋A $ .
若 $ a=0 $ ,则 $ B=\mathrm{⌀} $ ,满足 $ B⫋A $ .
当 $ a\ne 0 $ 时, $ B={x|x=\dfrac{2}{a}} $ ,
所以 $ \dfrac{2}{a}=2 $ 或 $ \dfrac{2}{a}=-2 $ ,
解得 $ a=1 $ 或 $ a=-1 $ .
综上所述,实数 $ a $ 的所有可能取值构成的集合为 $ {-1 {\rm ,0} $ , $ 1} $ .
12.已知 $ p: $ “方程 $ a{x}^{2}+2x+1=0 $ 至少有一个负实根”,若 $ p $ 为真命题的一个必要不充分条件为 $ a\leqslant m+1 $ ,则实数 $ m $ 的取值范围是 .
解析:若 $ p: $ “方程 $ a{x}^{2}+2x+1=0 $ 至少有一个负实根”为真命题,
则当 $ a=0 $ 时, $ 2x+1=0 $ ,则 $ x=-\dfrac{1}{2} $ ,符合要求;
当 $ a < 0 $ 时, $ \mathrm{\Delta }=4-4a > 0 $ ,设此时方程的两根分别为 $ {x}_{1} $ , $ {x}_{2} $ ,则 $ {x}_{1}+{x}_{2}=-\dfrac{2}{a} > 0 $ , $ {x}_{1}{x}_{2}=\dfrac{1}{a} < 0 $ ,因此方程 $ a{x}^{2}+2x+1=0 $ 有一个正根和一个负根,符合要求;
当 $ a > 0 $ 时,由 $ \mathrm{\Delta }=4-4a=0 $ ,解得 $ a=1 $ ,
此时方程为 $ {x}^{2}+2x+1={\left(x+1\right) ^ {2}}=0 $ ,解得 $ x=-1 $ ,符合要求,
由 $ \mathrm{\Delta }=4-4a > 0 $ 解得 $ 0 < a < 1 $ ,设此时方程的两根分别为 $ {x}_{3} $ , $ {x}_{4} $ ,则 $ {x}_{3}+{x}_{4}=-\dfrac{2}{a} < 0 $ , $ {x}_{3}{x}_{4}=\dfrac{1}{a} > 0 $ ,此时方程 $ a{x}^{2}+2x+1=0 $ 有两个不相等的负根,符合要求.
综上所述, $ p $ 为真命题时, $ a $ 的取值范围为 $ {a|a\leqslant 1} $ .
若 $ p $ 为真命题的一个必要不充分条件为 $ a\leqslant m+1 $ ,则 $ m+1 > 1 $ ,解得 $ m > 0 $ ,
因此实数 $ m $ 的取值范围为 $ {m|m > 0} $ .
13.已知集合 $ A={x|x < a $ 或 $ x > a+2} $ , $ B={x|x\geqslant 3} $ .
(1) 若“ $ x\in A $ ”是“ $ x\in B $ ”成立的必要条件,求实数 $ a $ 的取值范围;
(2) 若“ $ x\in A $ ”是“ $ x\in B $ ”成立的必要不充分条件,求实数 $ a $ 的取值范围;
(3) 若“ $ x\in {\complement }_{\boldsymbol{R}}A $ ”是“ $ x\in B $ ”成立的充分条件,求实数 $ a $ 的取值范围;
(4) 若“ $ x\in {\complement }_{\boldsymbol{R}}A $ ”是“ $ x\in B $ ”成立的充分不必要条件,求实数 $ a $ 的取值范围.
答案:(1) 【解】若“ $ x\in A $ ”是“ $ x\in B $ ”成立的必要条件,则 $ B $ 是 $ A $ 的子集,故 $ a+2 < 3 $ ,解得 $ a < 1 $ .
所以实数 $ a $ 的取值范围是 $ {a|a < 1} $ .
(2) 【解】若“ $ x\in A $ ”是“ $ x\in B $ ”成立的必要不充分条件,则 $ B $ 是 $ A $ 的真子集,故 $ a+2 < 3 $ ,
解得 $ a < 1 $ .
所以实数 $ a $ 的取值范围是 $ {a|a < 1} $ .
(3) 【解】若“ $ x\in {\complement }_{\boldsymbol{R}}A $ ”是“ $ x\in B $ ”成立的充分条件,则 $ {\complement }_{\boldsymbol{R}}A $ 是 $ B $ 的子集.
易知 $ {\complement }_{\boldsymbol{R}}A={x|a\leqslant x\leqslant a+2} $ ,所以 $ a\geqslant 3 $ .
所以实数 $ a $ 的取值范围是 $ {a|a\geqslant 3} $ .
(4) 【解】若“ $ x\in {\complement }_{\boldsymbol{R}}A $ ”是“ $ x\in B $ ”成立的充分不必要条件,则 $ {\complement }_{\boldsymbol{R}}A $ 是 $ B $ 的真子集.
因为 $ {\complement }_{\boldsymbol{R}}A={x|a\leqslant x\leqslant a+2} $ ,所以 $ a\geqslant 3 $ .
所以实数 $ a $ 的取值范围是 $ {a|a\geqslant 3} $ .
解析:
14.甲:“实数 $ a $ , $ b $ , $ c $ 满足 $ 2b=a+c $ ”,乙:“实数 $ a $ , $ b $ , $ c $ 满足 $ \dfrac{a}{b}+\dfrac{c}{b}=2 $ ”,则甲是乙的( )
A.必要不充分条件
B.充分不必要条件
C.充要条件
D.既不充分也不必要条件
答案:A
解析:当 $ a=b=c=0 $ 时,实数 $ a $ , $ b $ , $ c $ 满足 $ 2b=a+c $ ,但此时 $ \dfrac{a}{b}+\dfrac{c}{b}=2 $ 不成立;反过来由 $ \dfrac{a}{b}+\dfrac{c}{b}=2 $ 得 $ a+c=2b $ .
综上所述,“实数 $ a $ , $ b $ , $ c $ 满足 $ 2b=a+c $ ”是“实数 $ a $ , $ b $ , $ c $ 满足 $ \dfrac{a}{b}+\dfrac{c}{b}=2 $ ”的必要不充分条件,故选 $ \mathrm{A} $ .
15.已知 $ p:a=b $ , $ q:|a|=|b| $ ,则下列说法正确的是( )(多选)
A. $ q $ 是 $ p $ 的充分不必要条件
B. $ p $ 是 $ q $ 的充分不必要条件
C. $ q $ 的必要不充分条件是 $ p $
D. $ p $ 的必要不充分条件是 $ q $
答案:BD
解析:由 $ a=b $ ,得 $ |a|=|b| $ ,所以 $ p $ 是 $ q $ 的充分条件, $ p $ 的必要条件是 $ q $ ,
由 $ |a|=|b| $ ,得 $ a=±b $ ,所以 $ p $ 是 $ q $ 的不必要条件, $ p $ 的不充分条件是 $ q $ ,
所以 $ p $ 是 $ q $ 的充分不必要条件, $ p $ 的必要不充分条件是 $ q $ .故选 $ \mathrm{B}\mathrm{D} $ .
16.求证:一元二次方程 $ a{x}^{2}+bx+c=0 $ 有一正根和一负根的充要条件是 $ ac < 0 $ .
答案:【证明】充分性: $ \because ac < 0 $ , $ \therefore $ 一元二次方程 $ a{x}^{2}+bx+c=0 $ 的判别式 $ \mathrm{\Delta }={b}^{2}-4ac > 0 $ , $ \therefore $ 方程一定有两个不等实根,分别设为 $ {x}_{1} $ , $ {x}_{2} $ ,则 $ {x}_{1}{x}_{2}=\dfrac{c}{a} < 0 $ , $ \therefore $ 方程的两根异号,即方程 $ a{x}^{2}+bx+c=0 $ 有一正根和一负根.
必要性: $ \because $ 一元二次方程 $ a{x}^{2}+bx+c=0 $ 有一正根和一负根,分别设为 $ {x}_{1} $ , $ {x}_{2} $ ,则由一元二次方程根与系数的关系,得 $ \mathrm{\Delta }={b}^{2}-4ac > 0 $ 且 $ {x}_{1}{x}_{2}=\dfrac{c}{a} < 0 $ ,解得 $ ac < 0 $ .
综上可知,一元二次方程 $ a{x}^{2}+bx+c=0 $ 有一正根和一负根的充要条件是 $ ac < 0 $ .
解析:
17.“关于 $ x $ 的方程 $ a{x}^{2}+x-1=0 $ 的根为正实数”为真命题的一个必要不充分条件是( )
A. $ a=0 $
B. $ a\leqslant 0 $
C. $ -\dfrac{1}{4}\leqslant a\leqslant 0 $
D. $ -\dfrac{1}{4}\leqslant a < 0 $
答案:B
解析:关于 $ x $ 的方程 $ a{x}^{2}+x-1=0 $ 的根为正实数,
则需满足 $ a=0 $ 或 $ \begin{cases}a\ne 0,\\ \mathrm{\Delta }=1+4a\geqslant 0,\\ -\dfrac{1}{a} > 0,\end{cases} $ 解得 $ -\dfrac{1}{4}\leqslant a\leqslant 0 $ .
“关于 $ x $ 的方程 $ a{x}^{2}+x-1=0 $ 的根为正实数”为真命题的一个必要不充分条件设为 $ p $ , $ p $ 对应的集合为 $ B $ ,
则 $ {a|-\dfrac{1}{4}\leqslant a\leqslant 0}⫋B $ ,
结合选项可知 $ a\leqslant 0 $ 满足,故选 $ \mathrm{B} $ .
 或
或